
- •Лабораторна робота №1
- •Теоретичні відомості
- •Завдання для виконання
- •Int main()
- •Int main()
- •Лабораторна робота №2
- •Теоретичні відомості
- •Void main()
- •Void main()
- •Int k,m; //опис змінних
- •Void main()
- •Int k,m; //опис змінних
- •Void main()
- •Int k,m; //опис змінних
- •Void main()
- •Int k,m; //опис змінних
- •Завдання для виконання
- •Лабораторна робота №3
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main()
- •Void main()
- •Int main()
- •Завдання для виконання
- •Лабораторна робота №4
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main ( )
- •Void main ( )
- •Завдання для виконання
- •Лабораторна робота №5
- •Теоретичні відомості
- •Void main()
- •Void main()
- •Приклади виконання завдання
- •Void main ( )
- •Void main ( )
- •Завдання для виконання
- •Лабораторна робота №6
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main ( )
- •Void main ( )
- •Void main ( )
- •Завдання для виконання
- •Лабораторна робота №7
- •Теоретичні відомості
- •Void fact(int k);
- •Void fact(k);
- •Int *I; //Вказівник - змінна на дані типу int
- •Int k, *vk; //Опис змінної - вказівника *vk
- •Приклади виконання завдання лабораторної роботи
- •Int fact(int n)// Функція, що обчислює n!
- •Void dryk(int Cnm) /* Функція, що виводить на екран значення Cnm */
- •Void main ( )
- •Int Factorial(int n) /*Рекурсивна функція,що обчислює n! */
- •Void main()
- •Void Vs(double &V, double &s, double r)
- •Void main ( )
- •Void Vs(double *V, double *s, double r)
- •Void main ( )
- •Void main()
- •Завдання для виконання
- •Лабораторна робота №8
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main()
- •Void main()
- •Void main()
- •Завдання для виконання
- •Лабораторна робота №9
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main()
- •If (!feof(f1))
- •Void main()
- •Void main()
- •Void main()
- •Void main ()
- •Void main ()
- •Ifstream in( "vvid" );
- •In.Close();
- •Завдання для виконання
- •Лабораторна робота №10
- •Теоретичні відомості
- •Char st[40]
- •Char st3[100]
- •Char str4[100]
- •Приклади виконання завдання
- •Void main()
- •Void insert (char *str, int p, char c)
- •Void main()
- •Insert(s,n,c);
- •Void main()
- •Завдання для виконання
- •Лабораторна робота 11
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void main()
- •If(!strcmp(ms[I].Ngr,"m21"))
- •Завдання для виконання
- •Лабораторна робота 12
- •Теоретичні відомості
- •Void show_complex() /*вивід комплекснеого числа на екран */
- •Void show_complex();
- •Void complex::show_complex()
- •Void main()
- •Приклади виконання завдання
- •Завдання для виконання
- •Лабораторна робота 13
- •Теоретичні відомості
- •Приклади виконання завдання
- •Void operator --();
- •Void operator --(int);
- •Void show_complex();
- •Завдання для виконання
- •Завдання для самостійного виконання
- •Додаток №2. Базові типи даних
- •Додаток №3. Основні специфікатори формату функції printf
- •Додаток №5. Основні математичні функції бібліотеки math.H
- •Додаток №6.
- •Додаток №7. Можливі специфікатори аргументу mode
- •Додаток №8. Основні функції для роботи із рядковими змінними бібліотеки string.H
- •Додаток №9. Основні функції для роботи із символами бібліотеки ctype.H
- •Література
- •Ткачук Валерій Михайлович
- •Лабораторний практикум
- •76000, М. Івано-Франківськ, вул. С. Бандери, 1
Void main ( )
{
int i;
SetConsoleOutputCP(1251);
SetConsoleCP(1251);
double ai,s;
double eps;
cout << "\nВведіть бажану точність сумування ряду \n";
cin >>eps;
s=0;
i=1;
do
// тіло циклу з використанням оператора слідування
ai=pow(1.0/(2*i),i),s=s+ai,i=i+1;
while(ai>eps);
cout << "\nСума ряду рівна\t\t" << s;
cout<< "\nПросумовано " <<i<< " членів ряду " ;
cout << "\n ";
}
Результат роботи програми:
В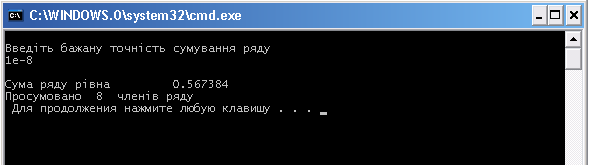 веденно
значення бажаної точності сумування
ряду eps=1e-8
веденно
значення бажаної точності сумування
ряду eps=1e-8
Приклад №3
Із клавіатури вводиться довільне ціле число, більше нуля. Визначити розрядність числа, максимальну цифру та кількість її входжень у число.
#include <stdio.h>
#include <math.h>
#include <windows.h>
Void main ( )
{
long int N,M,kilk=1;
int max,poz;
int i;
SetConsoleOutputCP(1251);
SetConsoleCP(1251);
printf("\n Введіть ціле число N>0\n");
scanf("%ld",&N);
M=N;
while(M/10>0)
{
kilk++;
M/=10;
}
printf("Число %ld має %ld розрядів \n ", N,kilk);
for (M=N, max=-1,poz=1,i=kilk;i>1;i--)
{
if(M%10>max)
{
max=M%10;
poz=i;
}
M/=10;
}
printf("Максимальною в числі %ld є цифра %d.\n", N, max);
M=N;
int j=0;
for (i=kilk; i>=1; i--)
{
if(M%10==max) j++;
M/=10;
}
printf("Вона входить у число %d разів\n",j);
}
Результат роботи програми:
В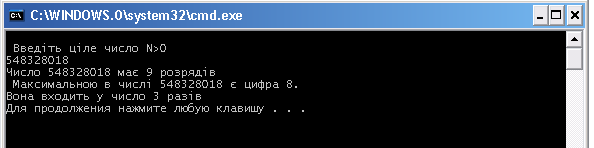 ведено
число 548328018
ведено
число 548328018
Завдання для виконання
Написати програму розв’язку завдання двома способами – із використанням оператора циклу while (перший спосіб) та за допомогою оператора циклу do…while (другий спосіб). Перевірити правильність виконання програми, використавши контрольні приклади.
Обчислити значення квадратного кореня
 із точністю
із точністю
 ,
використавши ітераційну формулу
Ньютона:
,
використавши ітераційну формулу
Ньютона:
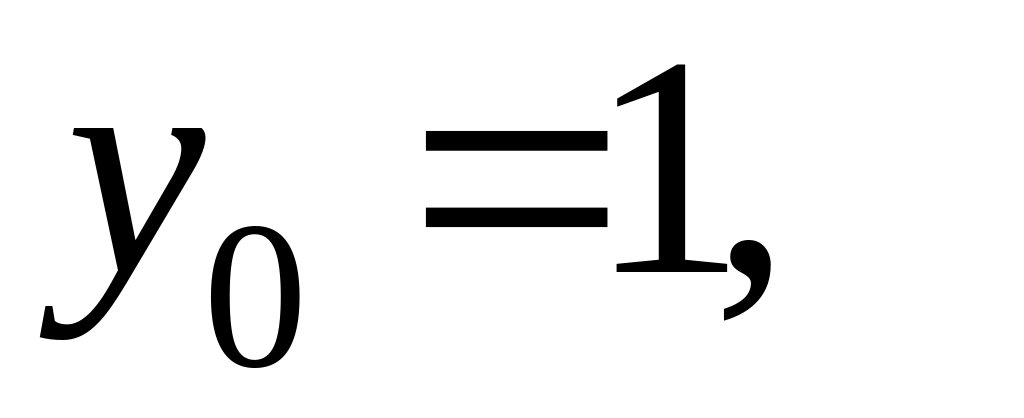
 .
Підрахувати кількість ітерацій, за
які досягається бажана точність.
Точність обчислення
визначається як модуль різниці двох
послідовних ітерацій.
.
Підрахувати кількість ітерацій, за
які досягається бажана точність.
Точність обчислення
визначається як модуль різниці двох
послідовних ітерацій.Обчислювати суму членів ряду, поки черговий член не стане меншим .
S=1 + 1/2 + 1/4 + 1/8 + ...
Обчислити значення кореня кубічного
 з точністю
,
використавши ітераційну формулу Ньютона
з точністю
,
використавши ітераційну формулу Ньютона
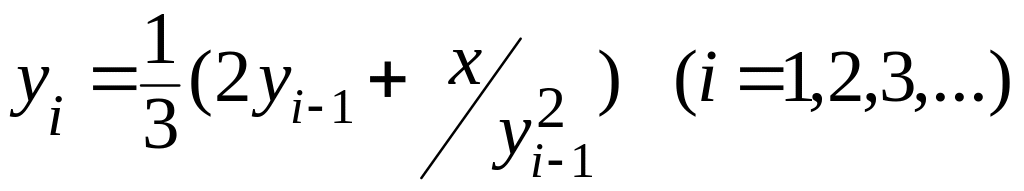 .
Підрахувати кількість ітерацій, за які
досягається бажана точність. Точність
обчислення
визначається як модуль різниці
двох послідовних ітерацій.
.
Підрахувати кількість ітерацій, за які
досягається бажана точність. Точність
обчислення
визначається як модуль різниці
двох послідовних ітерацій.
Значення функції
 можна обчислити її розкладом в ряд
Маклорена:
можна обчислити її розкладом в ряд
Маклорена:
![]()
Обчислити з точністю (обчислення продовжується до моменту, поки черговий член ряду по модулю не буде меншим ). Підрахувати кількість членів ряду, які просумовано для досягнення заданої точності.
Для двох натуральних чисел та (
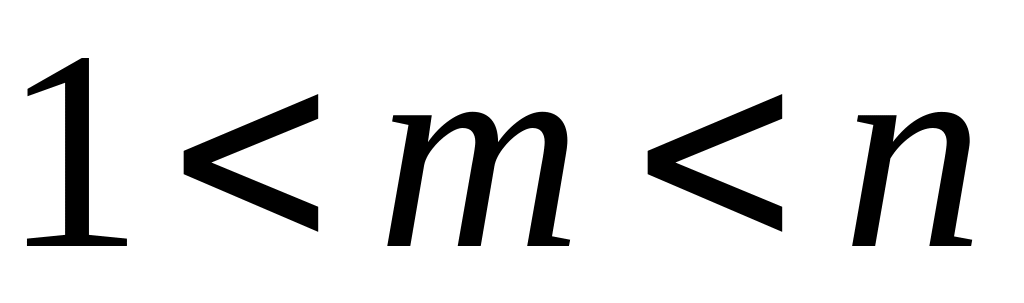 )
знайти найменше значення
,
при якому
)
знайти найменше значення
,
при якому
 .
.
Значення функції
 можна обчислити її розкладом в ряд
Маклорена
можна обчислити її розкладом в ряд
Маклорена
![]()
Обчислити з точністю (обчислення продовжується до моменту, поки абсолютне значення чергового члену ряду не буде меншим ). Підрахувати кількість членів ряду, які необхідні просумувати для досягнення заданої точності.
Знайти наближено з точністю 0.01 найбільше значення функції
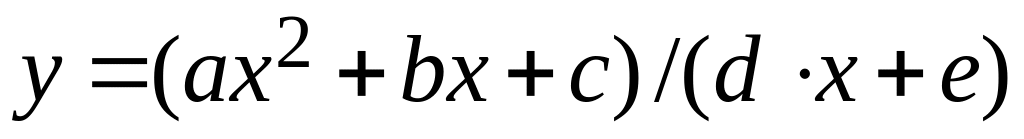 на відрізку
на відрізку
 (спосіб вибрати самостійно). Значення
(спосіб вибрати самостійно). Значення
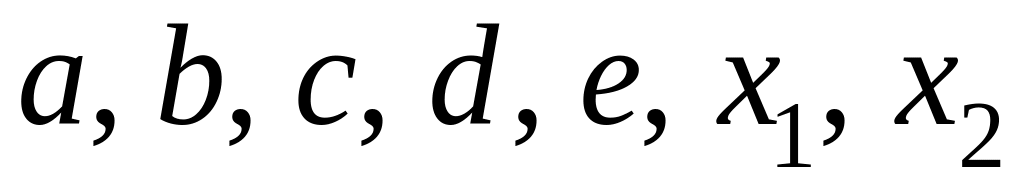 вводяться з клавіатури.
вводяться з клавіатури.
Для цілого числа
 отримати найбільше ціле
,
для якого
отримати найбільше ціле
,
для якого
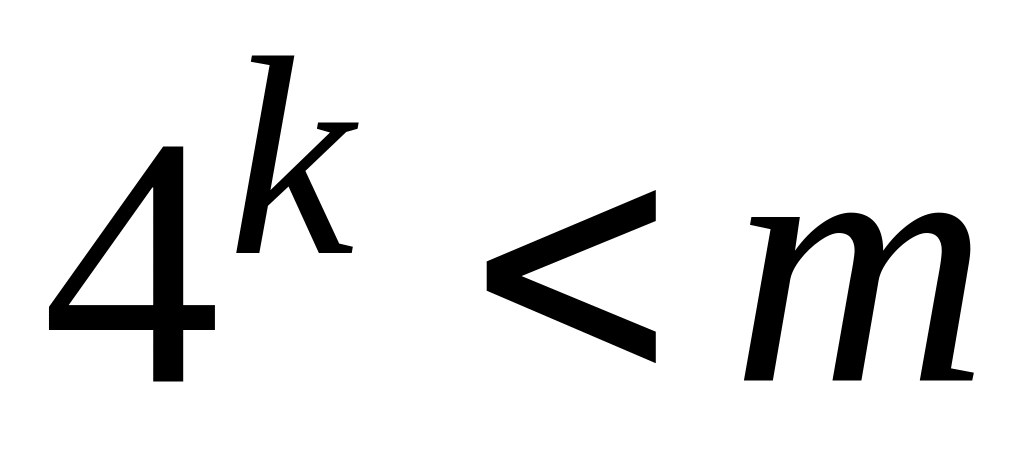 .
.Для натурального числа знайти найменше натуральне число виду
 ,
що перевищує
.
,
що перевищує
.Значення функції
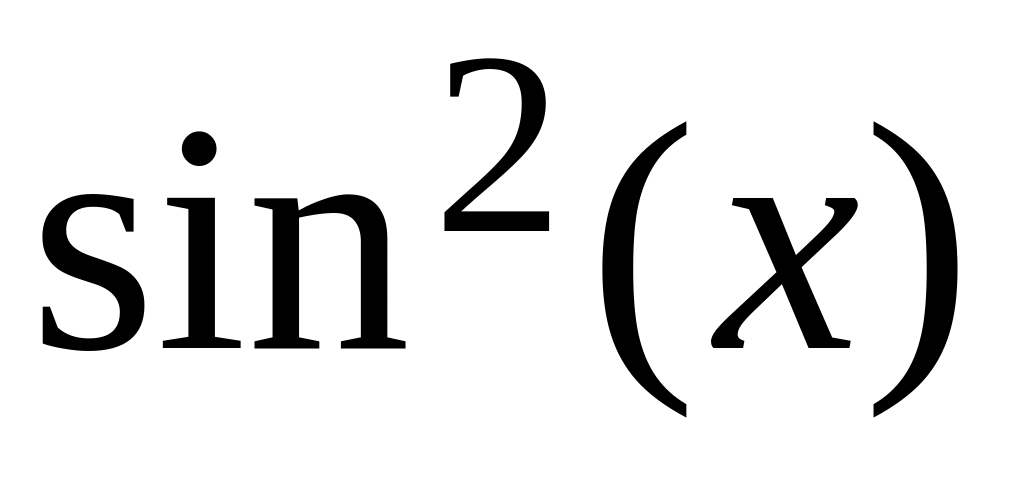 можна обчислити за допомогою її розкладу
в ряд Маклорена
можна обчислити за допомогою її розкладу
в ряд Маклорена
![]()
Обчислити з точністю ( обчислення продовжується до моменту, поки черговий член ряду по модулю не буде меншим ). Підрахувати кількість членів ряду, які необхідно просумувати для досягнення заданої точності.
Міняючи від початкового значення з кроком
 визначити, при якому значенні
добуток
визначити, при якому значенні
добуток
 стане більшим
.
Вхідні дані вводяться із клавіатури.
стане більшим
.
Вхідні дані вводяться із клавіатури.Знайти корінь рівняння
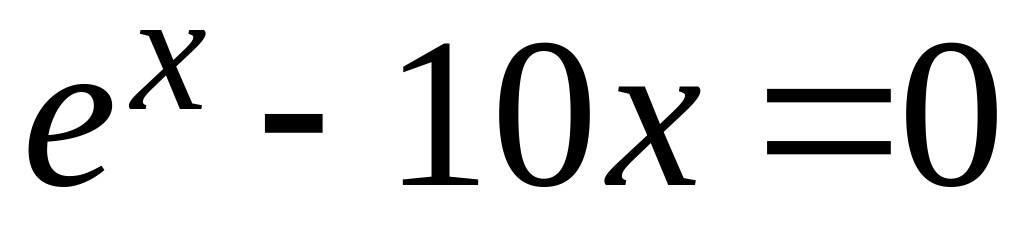 з точністю
методом простої ітерації.
з точністю
методом простої ітерації.Знайти корінь рівняння
 з точністю
методом простої ітерації.
з точністю
методом простої ітерації.Знайти корінь рівняння
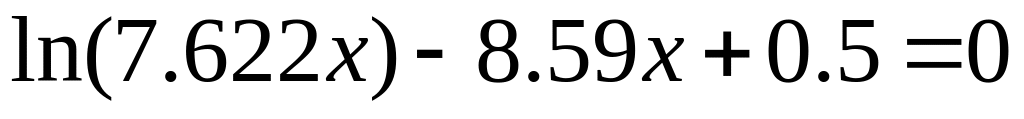 з точністю
методом простої ітерації.
з точністю
методом простої ітерації.Знайти корінь рівняння
 з точністю
методом простої ітерації.
з точністю
методом простої ітерації.Вивести значення функції
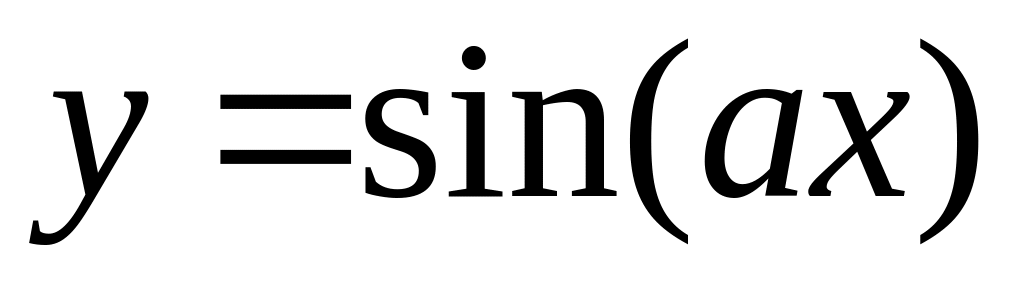 для
,
що міняються від 0 з кроком 0.05 до тих
пір, поки функція зростає. Значення
вводиться із клавіатури.
для
,
що міняються від 0 з кроком 0.05 до тих
пір, поки функція зростає. Значення
вводиться із клавіатури.Уточнити корінь рівняння на проміжку
 методом половинного ділення.
Ітераційний процес продовжується до
тих пір, поки величина проміжку не стане
меншою заданої величини
(0.001) (задається як константа).
методом половинного ділення.
Ітераційний процес продовжується до
тих пір, поки величина проміжку не стане
меншою заданої величини
(0.001) (задається як константа).
Обчислити значення числа , використавши приведену нижче формулу, із заданою точністю eps (0.001), введеною із клавіатури.
![]()
Обчислити значення числа , використавши приведену нижче формулу, із заданою точністю (0.0001), введеною із клавіатури.
![]()
Написати програму обчислення суми членів послідовності, яка задається формулою
![]()
Сумування
членів ряду проводити до тих пір, поки
![]()
![]() .
.
Написати програму обчислення суми членів послідовності, яка задається формулою
![]()
Сумування
членів ряду проводити до тих пір, поки
![]()
![]() .
.
Написати програму обчислення суми членів послідовності, яка задається формулою
![]()
Сумування
членів ряду проводити до тих пір, поки
![]()
![]() .
.
Написати програму обчислення суми членів послідовності, яка задається формулою
![]()
Сумування
членів ряду проводити до тих пір, поки
![]()
![]() .
.
Знайти корінь рівняння
 на проміжку
на проміжку
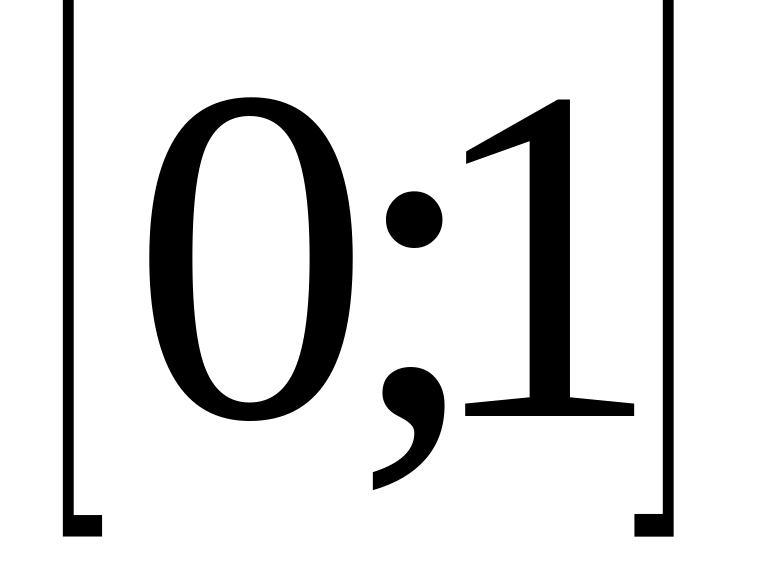 з точністю =0.001
методом половинного ділення.
з точністю =0.001
методом половинного ділення.Із клавіатури вводиться довільне ціле число. Підрахувати суму його цифр.
Знайти корінь рівняння
 на проміжку
на проміжку
 з точністю =0.005
методом половинного ділення.
з точністю =0.005
методом половинного ділення.Із клавіатури вводиться довільне ціле число. Отримати із нього нове число, в якому цифри слідують у зворотному порядку.
Написати програму обчислення суми членів ряду, -ний член якого задається формулою
![]()
Сумування
членів ряду проводити до тих пір, поки
![]()
![]() .
Підрахувати кількість просумованих
членів ряду.
.
Підрахувати кількість просумованих
членів ряду.
Знайти корінь рівняння
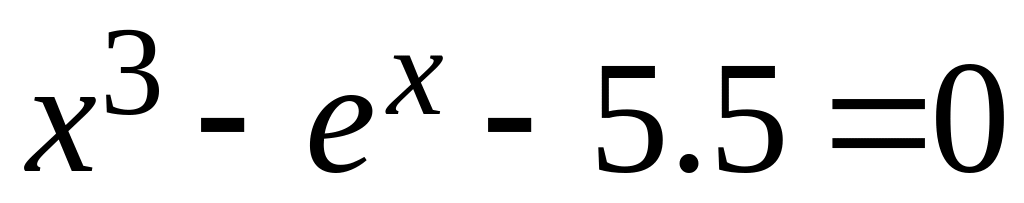 на проміжку
на проміжку
 з точністю =0.0001
методом половинного ділення.
з точністю =0.0001
методом половинного ділення.
