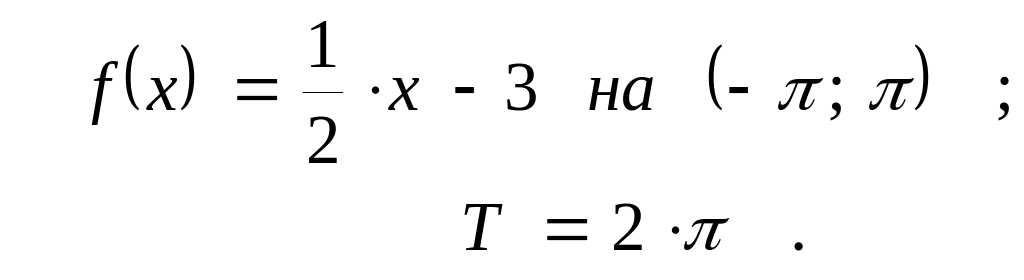Задача 5. Исследовать сходимость числовых рядов

1 .

2 .

4.3 .

4 .

5 .

6 .

7 .

8 .

6.9 .

10 .

11 .

12 .

6.13 .

14 .

15 .

16 .

17 .

18 .

19 .

20 .

21 .

22 .

23 .

24 .

25 .

26 .

27 .

28 .

29 .

30 .

31 .

32 .

33 .

34 .

35 .

36 .

Указание к выполнению

Использовать признак Даламбера.

Задача 6. Найти область сходимости ряда.

1 .

2 .

3 .

4 .

5 .

6 .

8.7 .

8 .

9 .

10 .

11 .

12 .

8.13 .

14 .

15 .

16 .

17 .

18 .

19 .

20 .

8.21 .

22 .

23 .

24 .

25 .

26 .

27 .

28 .

29 .

30 .

31 .

32 .

33 .

34 .

35 .

36 .

Указание к выполнению

1. Для степенного ряда вида

в случае, когда все коэффициенты ряда (т.е. ряд содержит все целые положительные степени выражения ), интервал сходимости определяется неравенством

где радиус сходимости определяется по формуле Даламбера (2) или по формуле Коши (3):

2. Если же степенной ряд содержит не все целые положительные степени выражения (например, степенной ряд содержит члены только с четными или только с нечетными степенями выражения ),

то

в этом случае степенной ряд рассматривается как функциональный ряд общего вида

,

интервал сходимости которого определяется с помощью признака Даламбера (4) или признака Коши (5) (применяемых к ряду ):

.

3. Исследовать сходимость степенного ряда в граничных точках интервала сходимости.

Задача 7.

Разложить в ряд Фурье функцию с периодом ;

при этом,

если функция задана на полупериоде (т.е. на промежутке, длина которого равна половине периода ), то разложить в ряд Фурье по синусам или по косинусам.

1

2

3

4

5

6

7

8

9	10
11	12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

Указание к выполнению

Использовать формулы разложений в ряд Фурье:

• периодических функций с произвольным периодом ;

• с периодом ;

• четных и нечетных функций;

• функций, заданных на полупериоде.

Задача 8. Найти все значения корня из комплексного числа.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

Задача 9. Решить задачи операционного исчисления

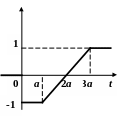
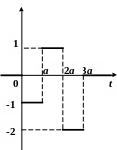
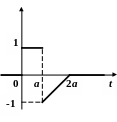
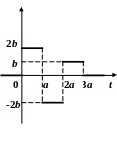
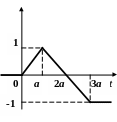
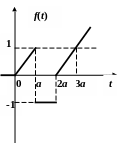
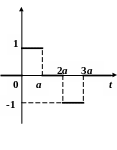
По данному графику оригинала найти изображение.

1 f(t)	2		3
4 f(t)	5		6
7 f(t)	8		9
10 f(t)	11		12
13 f(t)	14		15
16 f(t)	17		18
19 f(t)	20		21
22 f(t)	23		24
25	26		27
28 f(t)	29		30
31
32 f(t)	33		34
35 f(t)	36

ПРИЛОЖЕНИЕ

Ряды Фурье

1. Определение (Условия Дирихле)

Говорят, что функция удовлетворяет условиям Дирихле в интервале длины , если в этом интервале:

1. функция кусочно-монотонна (имеет конечное число экстремумов);

2. функция непрерывна, за исключением конечного числа точек разрыва первого рода, т.е. в точках существуют конечные пределы:

,

.

2. Определение (Ряд Фурье)

Рядом Фурье периодической функции с периодом называется тригонометрический ряд

,

где

Числа называют коэффициентами Фурье.

В частности, для периодической функции с периодом (т.е. ) ряд Фурье имеет вид

,

где

3. Замечание

Можно показать, что интеграл от периодической функции по любому отрезку, длина которого равна длине периода, имеет всегда одно и то же значение.

Поэтому коэффициенты Фурье периодической функции периода можно записать в виде:

где любое действительное число.

4. Теорема (Дирихле)

Если периодическая функция (периода ) удовлетворяет в интервале условиям Дирихле, то ряд Фурье функции сходится для любого , его сумма равна:

1. , т.е.

,

для всех точек, в которых функция непрерывна;

2. ,

где точка разрыва 1-го рода функции ;

3. 

— на концах промежутка.

5. Замечание

Если доопределить функцию в точках разрыва и на концах промежутка соответствующими значениями суммы ряда Фурье ,

т.е. принять

;

,

то можно считать, что при выполнении условий Дирихле ряд Фурье функции сходится к ней для любого :

6. Ряд Фурье для четных функций

Если — четная функция периода , то:

;

.

Ряд Фурье для четной функции содержит только свободный член и косинусы:

Ряд Фурье для четной функции периода имеет вид:

,

где

.

7. Ряд Фурье для нечетных функций

Если — нечетная функция периода , то:

;

.

Ряд Фурье для нечетной функции содержит только синусы:

Ряд Фурье для нечетной функции периода имеет вид:

,

где

.