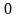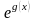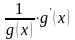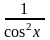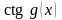6.8. Асимптоты графика функции

Асимптотой линии называют прямую, к которой неограниченно приближается данная линия, когда ее точка неограниченно удаляется от начала координат.

Виды асимптот:

1) вертикальные – параллельные оси Оу;

2) наклонные – пересекающие ось Оу;

3) горизонтальные – параллельные оси ОУ.

1. Уравнение вертикальной асимптоты графика функции имеет вид , при условии, что выполняется хотя бы одно из условий: , .

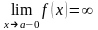2. Уравнение наклонной асимптоты графика функции имеет вид , где

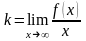, (6.18)

. (6.19)

3. Если , то имеем горизонтальную асимптоту .

7. Производная функции одной переменной

7.1. Определение производной

Производной функции в данной точке называют предел отношения приращения функции к соответствующему приращению ее аргумента при условии, что последнее стремится к нулю:

. (7.1)

Производная функции показывает скорость изменения функции при изменении ее аргумента.

Дифференциал функции находят по формуле:

, (7.2)

где .

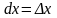7.2. Правила дифференцирования

Операцию нахождения производной называют дифференцированием.

Основные правила дифференцирования:

, где – число; (7.3)

, где , ; (7.4)

; (7.5)

; (7.6)

. (7.7)

7.3. Производные элементарных и сложных функций

Таблица производных элементарных и сложных функций:

Функция	Производная	Функция	Производная
х	1
x n	nx n-1
tg x
ctg x
arctg x

Пример 1. Найдите производную функции .

Решение. Согласно правилу запишем:

, .

Так как постоянный множитель можно выносить за знак производной, то получим: .

Используя таблицу производных, будем иметь:

.

Ответ: .

Пример 2. Вычислите значение дифференциала функции , если х изменяется от 10 до 10,01.

Решение. 1. Найдем производную функции:

.

2. Согласно формуле 7.2 запишем дифференциал функции:

.

3. Так как согласно условию задачи , а , то .

Ответ: 2.

Пример 3. Найдите дифференциал функции .

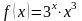Решение. Применяя правило дифференцирования

,

и используя таблицу производных, получим:

.

Запишем: .

Ответ: .

Пример 4. Найдите производную функции .

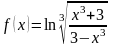Решение. Запишем функцию в виде:

, .

Вынося постоянный множитель за знак производной, и, применяя правило дифференцирования сложной функции

,

получим:

, , , .

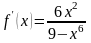Ответ: .

Пример 5. Найдите производную функции .

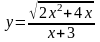Решение. Применяя правила и , получим:

, , , . Ответ: .

Пример 6. Найдите , если .

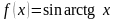Решение. Применяя правила

и ,

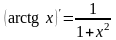получим: , .

Тогда .

Ответ: 1.