
- •2. Полагая , запишем:
- •5.4. Взаимное расположение прямых в пространстве
- •5.5. Взаимное расположение прямой и плоскости
- •5.6. Расстояние от точки до плоскости
- •6. Функции
- •6.2. Функция: основные понятия и определения
- •6.8. Асимптоты графика функции
- •7. Производная функции одной переменной
- •7.1. Определение производной
- •7.2. Правила дифференцирования
- •7.3. Производные элементарных и сложных функций
- •7.4. Производная неявной функции
- •7.5. Производная функции, заданной параметрически
- •7.6. Производная показательно-степенной функции
- •7.7. Производные и дифференциалы высших порядков
- •8. Исследование функции с помощью производной
- •8.1. Основные теоремы о дифференцируемых функциях
- •8.2. Геометрический и физический смысл производной
- •8.3. Исследование функции с помощью производной
- •8.4. Исследование функции с помощью второй
- •8.5. Исследование функции и построение графика
Ответ:
 .
.
Пример
8. Запишите каноническое уравнение
прямой

Решение. Найдем две любые точки, принадлежащие этой прямой.
1. Полагая
 ,
запишем:
,
запишем:

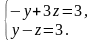
Складывая эти
уравнения, получим
 ,
откуда
,
откуда
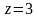 .
Тогда
.
Тогда
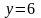 .
Получили точку
.
Получили точку
 .
.
2. Полагая , запишем:
Складывая эти
уравнения, получим
 ,
откуда
,
откуда
 .
Тогда
.
Тогда
 .
Получили точку
.
Получили точку
 .
.
3. Согласно формуле 5.11 запишем:
 ,
,
 ,
,
 .
.
Ответ: .
5.4. Взаимное расположение прямых в пространстве
Рассмотрим две прямые, записанные в каноническом виде
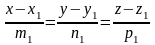 и
и
 ,
,
где
 и
и
 – точки,
принадлежащие этим прямым, а
– точки,
принадлежащие этим прямым, а
 и
и
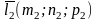 – направляющие векторы этих прямых.
– направляющие векторы этих прямых.
1. Прямые параллельны, если параллельны их направляющие векторы:
 .
(5.13)
.
(5.13)
Но направляющие
векторы прямых не должны быть параллельны
вектору
 .
.
2. Прямые перпендикулярны, если перпендикулярны их направляющие векторы:
 (5.14)
(5.14)
3.
Если прямые образуют угол
 ,
то
,
то
 .
(5.15)
.
(5.15)
4.
Прямые скрещиваются,
если они лежат в разных плоскостях, то
есть векторы
 ,
,
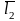 и
и
 не компланарны:
не компланарны:
 .
(5.16)
.
(5.16)
Пример
9. Установите взаимное расположение
прямых
 и
и
 .
.
Решение.
1. Согласно условию запишем:
 ,
,
 ,
,
 ,
,
 .
.
2. Выясним, являются
ли прямые параллельными:
 .
Так как не выполняется условие 5.13, то
данные прямые не параллельны.
.
Так как не выполняется условие 5.13, то
данные прямые не параллельны.
3. Выясним, являются ли прямые скрещивающимися:
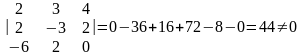 .
.
Так как выполняется условие 5.16, то данные прямые скрещиваются.
Ответ: прямые скрещиваются.
Пример
10. Найдите угол между прямыми
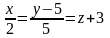 и
и
 .
.
Решение. 1. Запишем направляющие векторы этих прямых:
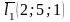 и
и
 .
.
2. Найдем скалярное произведение направляющих векторов:
 .
.
Так как эти прямые
перпендикулярны, то
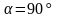 .
.
Ответ:
 .
.
5.5. Взаимное расположение прямой и плоскости
Рассмотрим прямую
 и плоскость
и плоскость
 .
.
1. Прямая параллельна плоскости, если
 .
(5.17)
.
(5.17)
2. Прямая перпендикулярна плоскости, если
 .
(5.18)
.
(5.18)
3. Если прямая образует с плоскостью угол , то
 .
(5.19)
.
(5.19)
Пример
11. Найдите значение p,
при котором прямая
 параллельна плоскости
параллельна плоскости
 .
.
Решение. Согласно условию задачи запишем:
 ,
,
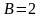 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Подставляя эти значения в формулу 5.17, получим:
 ,
откуда
,
откуда
 .
.
Ответ: 3.
5.6. Расстояние от точки до плоскости
Расстояние от
точки
 до плоскости
до плоскости
с
нормальным вектором
 находят по
формуле:
находят по
формуле:
 .
(5.20)
.
(5.20)
Пример
12. Найдите расстояние между плоскостями
 и
и
 .
.
Решение.
1. Данные плоскости параллельны, так как
выполняется условие 5.6:
 .
.
2. Найдем любую
точку, принадлежащую первой плоскости.
Например, полагая
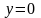 ,
а
,
а
 ,
получим
.
,
получим
.
2. Найдем расстояние
от точки
 до плоскости
до плоскости
 .
Согласно формуле 5.20 запишем:
.
Согласно формуле 5.20 запишем:
 .
.
Ответ:
 .
.
Контрольный тест 5
Укажите правильный вариант ответа (1 – 10):
1.
Если точка
 принадлежит плоскости
принадлежит плоскости
,
а
вектор
 – нормальный вектор этой плоскости, то
значение D равно
– нормальный вектор этой плоскости, то
значение D равно
Варианты ответов: 1) 0; 2) 14; 3) – 8; 4) – 24; 5) 24.
2.
Если плоскость проходит через точки
 ,
,
 и
и
 ,
то сумма координат нормального вектора
этой плоскости равна
,
то сумма координат нормального вектора
этой плоскости равна
Варианты ответов: 1) 4; 2) 9; 3) 0; 4) – 4; 5) 17.
3.
Если
 – нормальный вектор плоскости
,
а
– нормальный вектор плоскости
,
а
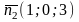 – нормальный вектор плоскости
– нормальный вектор плоскости
 ,
то угол между этими плоскостями равен
,
то угол между этими плоскостями равен
Варианты ответов:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
4.
Расстояние от точки
 до плоскости
до плоскости
 равно
равно
Варианты ответов:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
5.
Плоскости
 и
и
 перпендикулярны при условии, что значение
n
равно
перпендикулярны при условии, что значение
n
равно
Варианты ответов: 1) – 2; 2) 1; 3) 0; 4) 4; 5) – 5.
6.
Если прямая
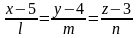 параллельна вектору
параллельна вектору
 и проходит через точку
и проходит через точку
 ,
то значение выражения
,
то значение выражения
 равно
равно
Варианты ответов: 1) 10; 2) 15; 3) – 24; 4) 24; 5) – 6.
7.
Если прямая
перпендикулярна векторам
 и
и
 ,
то она параллельна вектору
,
то она параллельна вектору
Варианты ответов:
1)
 ;
2)
;
2)
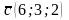 ;
3)
;
3)
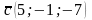 ;
4)
;
4)
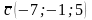 ;
5)
;
5)
 .
.
8.
Если точки
 ,
,
 ,
,
 и
и
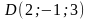 – вершины пирамиды, то абсолютная
величина скалярного произведения
нормальных векторов граней ABC
и ADC
равна
– вершины пирамиды, то абсолютная
величина скалярного произведения
нормальных векторов граней ABC
и ADC
равна
Варианты ответов: 1) 3; 2) 0; 3) 1; 4) – 6; 5) 33.
9. Если точки , , и – вершины пирамиды, то угол между гранями ABC и ADC равен
Варианты ответов:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 .
.
10. Если точки , , и – вершины пирамиды, то прямая AD образует с гранью ABC угол, величина которого равна
Варианты ответов:
1)
;
2)
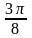 ;
3)
;
3)
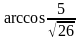 ;
4)
;
5)
;
4)
;
5)
 .
.
