3.4. Скалярное произведение векторов
Скалярным произведением векторов и является число, которое находят по формуле:
,
(3.8)
если
известны длины
и
векторов
и
и величина α
угла между ними
или по формуле:
,
(3.9)
если
известны координаты векторов
и
.
Например:
1) Найдем скалярное произведение векторов
и
,
если известно, что
,
и
.
Согласно формуле 3.8 запишем:
.
2) Найдем скалярное
произведение векторов
и
.
Согласно формуле 3.9 запишем:
.
Скалярным квадратом вектора называют скалярное произведение вектора на себя:
.
(3.10)
Например,
найдем скалярный квадрат вектора
.
Так как
,
то
и
.
Угол между векторами и находят по формуле:
.
(3.11)
Пример
4. Найдите
внутренний угол С
треугольника ABC
(рис. 3.12), зная координаты его вершин:
,
,
.
|
Решение.
1) Найдем координаты векторов
|
Рис. 3.12 |
и
,
вычитая из координат концов векторов
соответствующие координаты их начал:
,
.
2) По формуле найдем длины векторов и :
,
.
3) По формуле 3.9 найдем скалярное произведение векторов и :
.
4) Согласно формуле 3.11 запишем:
,
,
откуда
.
Ответ:
.
Векторы
и
перпендикулярны,
если угол между ними равен
.
Поскольку
,
то скалярное произведение перпендикулярных
векторов равно нулю.
Пример
5. Найдите
координаты векторов
и
,
зная, что угол между ними равен
.
Решение. Так как векторы и перпендикулярны, то их скалярное произведение равно нулю:
,
,
и
.
Тогда:
и
.
Ответ: и .
Если векторы
и
образуют угол
,
то проекцию
вектора
на вектор
находят по формуле:
или
(3.12)
3.5. Векторное произведение векторов
Рассмотрим векторы и .
Векторным произведением векторов и называют третий вектор , который перпендикулярен как вектору , так и вектору .
Векторное произведение векторов и находят по формуле:
(3.13)
Площадь параллелограмма, построенного на векторах и , находят по формуле:
,
(3.14)
Площадь треугольника, построенного на этих же векторах, находят по формуле:
,
(3.15)
Пример
6. Найдите
площадь треугольника с вершинами в
точках
,
и
.
Решение.
1. Найдем координаты векторов
и
.
Получим:
;
.
2. По формуле 3.13 найдем векторное произведение векторов и :
.
3. По формуле 3.2 найдем модуль вектора :
.
4. По формуле 3.15
найдем площадь треугольника:
.
Ответ:
.
3.6. Смешанное произведение векторов
Рассмотрим векторы
,
и
Смешанным произведением этих векторов называют число, которое получено в результате скалярного умножения вектора на векторное произведение векторов и .
Смешанное произведение векторов и и находят по формуле:
(3.16)
Объем параллелепипеда, построенного на векторах , и , находят по формуле:
.
(3.17)
Объем пирамиды, построенной на векторах , и , находят по формуле:
.
(3.18)
Пример
7. Найдите
объем параллелепипеда, построенного
на векторах
,
и
.
Решение. 1. Найдем смешанное произведение данных векторов:
.
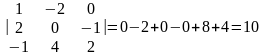2. Согласно формуле
3.17 получим:
.
Ответ: 10.
Контрольный тест 3
Укажите правильный вариант ответа (1 – 10):
1.
Серединой отрезка АВ,
если
и
,
является точка с координатами
Варианты ответов:
1)
;
2)
;
3)
;
4)
;
5)
.
2.
Длина вектора
равна
Варианты ответов:
1)
;
2) 8; 3)
;
4) 12; 5)
.
3.
Длина вектора
,
если
,
а
,
равна
Варианты ответов:
1)
;
2)
;
3)
;
4)
;
5) 1.
4. Коллинеарными являются векторы и
Варианты ответов:
1)
и
;
2)
и
;
3)
и
;
4)
и
;
5)
и
.
5. Скалярное произведение векторов
и
равно
Варианты ответов: 1) 2; 2) 6; 3) 1; 4) 3; 5) 10.
6. Косинус
угла между векторами
и
равен
Варианты ответов:
1)
;
2)
;
3)
;
4)
;
5)
.
7. Проекция
вектора
на вектор
равна
Варианты ответов:
1)
;
2)
;
3) 5; 4) 30; 5)
.
8.
Если векторы
и
перпендикулярны, то значение n
равно
Варианты ответов: 1) 5; 2) 8; 3) 1; 4) 0; 5) 7.
9.
Площадь треугольника с вершинами в
точках
;
и
равна
Варианты ответов:
1)
;
2)
;
3)
;
4)
;
5)
.
10.
Объем параллелепипеда, построенного
на векторах
,
и
,
равен
Варианты ответов: 1) 35; 2) 20; 3) 8; 4) 10; 5) 16.