3.2. Линейные действия с векторами

К линейным действиям с векторами относят сложение векторов, вычитание векторов и умножение вектора на число.

Сложение векторов на плоскости

На плоскости векторы складывают по правилу треугольника или по правилу параллелограмма.

1. Чтобы сложить векторы и по правилу треугольника, необходимо отложить вектор из конца вектора . Тогда суммой векторов и будет третий вектор 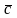, начало которого совпадает с началом вектора , а конец – с концом вектора .

На рисунке 3.7 .

2. Чтобы сложить векторы и по правилу параллелограмма, необходимо отложить вектор из начала вектора и на векторах и как на сторонах построить параллелограмм. Тогда суммой векторов и будет третий вектор , начало которого совпадает с началом векторов и , а конец вектора – с противолежащей вершиной параллелограмма.

На рисунке 3.8 .

Рис. 3.7	Рис. 3.8

Сумма противоположных векторов равна нулю:

, .

Вычитание векторов на плоскости

Чтобы вычесть из вектора вектор , можно заменить вычитание этих векторов сложением вектора и вектора :

.

На рисунке 3.9 векторы и сложены по правилу треугольника.

Рис. 3.9

Сложение векторов в пространстве

Чтобы сложить векторы в пространстве, необходимо выполнить их параллельный перенос в одну плоскость, если они не лежат в одной плоскости, и сложить эти векторы по правилу треугольника или по правилу параллелограмма.

Рис. 3.10	Рис. 3.11

Пример 3. На рисунке 3.10 изображен прямой параллелепипед. Найдите: ; ; ; .

Решение. 1) По правилу параллелограмма получим: .

2) По правилу треугольника получим: .

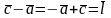3) Так как векторы и противоположны, то .

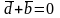4) Чтобы сложить векторы и , необходимо заменить вектор вектором (выполнить параллельный перенос вектора в плоскость, содержащую вектор ) и сложить векторы и по правилу треугольника: .

Ответ: ; ; 0; .

Сложение векторов с заданными координатами

Чтобы сложить (вычесть) векторы и , необходимо сложить (вычесть) их соответствующие координаты:

. (3.5)

Например, найдем разность векторов

и . Получим:

.

Умножение вектора на число

Чтобы умножить вектор на число k, необходимо каждую координату вектора умножить на это число:

. (3.6)

Например, умножим вектор на число – 3:

.

Сочетая действия сложения и вычитания векторов, а также умножение вектора на число, получим линейную комбинацию векторов.

Например, найдем вектор , если известно, что и . Получим:

.

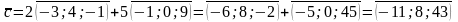3.3. Линейная зависимость векторов

Составим линейную комбинацию комбинация n-мерных векторов , , …, : .

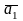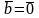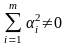Если и , то векторы линейно зависимы и не образуют базис.

Если и , то векторы линейно независимы и образуют базис.

Если векторы , и образуют базис, то определитель, составленный из координат этих векторов, не равен нулю:

(3.7)