Номера компонент

Рис. 5. Распределение весовых значений компонент

Интерпретация результатов факторного анализа означает перевод с одного языка на другой, в данном случае с языка цифр на язык слов, с языка статистики на язык социологии. Следует помнить, что факторный анализ — это не конец описания и объяс­нения результатов социологического исследования, а основа для формулирования гипотез, которые подлежат проверке, в том числе и путем повторного факторного анализа.

Выявив перечни переменных, относящихся к каждому фактору, мы должны проанализировать их содержание, подобрать обобщающее название для этого фактора. Подбор названия фактора означает поиск среди известных социологу понятий того понятия, которое в наибольшей степени соответствует конфигурации перемен­ных в их скоплении. Следует учитывать, что «матрица корреляций может быть факторизована (курсив мой. — Г.А.) бесчисленным ко­личеством способов» [Харман, 14]. Отбор наиболее подходящего способа осуществляется на основе содержательных критериев (концепции, гипотез, целей и задач исследования, сформулирован­ных в его программе). Поэтому чисто статистическая процедура всегда должна сопровождаться качественным анализом полученных результатов.

Знаки «плюс» и «минус» факторных значений интерпретируют­ся как увеличение или уменьшение значения переменной, т.е. про­сто как разные направления. «Знак факторных нагрузок сам по себе не имеет внутреннего содержания и не несет информации о зависимости между переменной и фактором. Однако стоит сопо­ставлять знаки разных переменных при одном факторе» [Фактор­ный, дискриминантный и кластерный анализ, 67]. Факторные на­грузки меньше 0,3 считаются несущественными [Там же, 60]. Ин­терпретация факторов сводится к анализу величины и знаков на­грузок. Рассмотрим эту процедуру на примере приведенного выше двухфакторного решения (см. рис. 3). Два выделенных фактора объясняют 61% дисперсии и включают переменные, указанные в табл. 5.

Выпишем наибольшие значения переменных по выделенным факторам. Фактор 1: отрицательное направление (взгляды Зюгано­ва, коммунистические взгляды, КПРФ), положительное направле­ние (взгляды Хакамады, либеральные, СПС). Фактор 2: отрица­тельное направление (ОВР, «Яблоко»), положительное направление (взгляды Путина, Яковлева). Содержание первого фактора составляет идеологический раскол (коммунисты — либералы), содержа­ние второго фактора — политический раскол (власть — оппози­ция). При интерпретации этих данных следует учитывать, что пе­тербургские сторонники ОВР и «Яблока» в основном голосовали против Путина на президентских выборах 2000 г., а само петербургское отделение «Яблока» (Региональная партия центра) находилось в оппозиции губернатору Яковлеву. Эти расколы определя­ли политическое поведение населения Санкт-Петербурга в 2000 г. (факторный анализ осуществлен на основе данных общегородского опроса, проведенного ЦЭПИ СПбГУ в ноябре 2000 г.).

Таблица 5

Значения переменных после вращения*

Переменные	Факторы
	1	2
Взгляды Зюганова	0,823	+0,368
Взгляды Путина	0,454	+0,777
Взгляды Хакамады	+0,776	+0,202
Взгляды Яковлева	0,340	+0,679
Взгляды Явлинского	+0,627	+0,261
«Единство»	+0,443	0,151
«Отечество— Вся Россия»	0,232	0,872
КПРФ	0,842	0,000
СПС	+0,884	+0,366
«Яблоко»	0,000	0,642
Коммунистические взгляды	0,898	+0,258
Социал-демократические взгляды	+0,427	0,000
Либеральные взгляды	+0,708	0,187

* Матрица получена методом главных компонент в пакете SPSS.

Кластерный анализ (от англ. cluster — пучок, группа) — это процедура, позволяющая классифицировать различные объекты. С его помощью можно разбить респондентов на группы, сходные по ряду признаков. На дендрограмме «дерева признаков» признаки соединяются линиями, образуя отдельные пучки («ветви»), связан­ные с другими пучками («ветвями»). Эти пучки и называют клас­терами. Чем короче линия, связывающая переменные, тем ближе они находятся в пространстве признаков. В процессе кластериза­ции происходит объединение сходных объектов во все более сложные группы («разветвление»). Кластерный анализ представляет собой разновидность многомерной статистической процедуры, упорядочивающей объекты в относительно однородные группы. Переменные для кластерного анализа выбираются в соответствии с теорией (концепции, гипотезы), которая лежит в основе классифи­кации [Факторный, дискриминантный, кластерный анализ, 153]. Перед началом анализа они должны быть преобразованы в бино­минальные, принимающие значение «1» при наличии признака и «0» при его отсутствии. В статистическом пакете SPSS эта опера­ция осуществляется в опции: transform\recode. Кроме того, из ана­лиза следует исключить альтернативы: «затрудняюсь ответить» «другое» и пр.

Важную роль в кластерном анализе играют «меры сходства» Наиболее часто в качестве такой меры употребляется коэффициент корреляции Пирсона, первоначально использовавшийся для опре­деления зависимости переменных. Кластеры обладают рядом свойств, среди которых наиболее важными являются плотность, дисперсия, форма, отдельность. Плотность — это близость отдель­ных точек скопления, позволяющая отличать его от других облас­тей многомерного пространства, содержащих либо мало точек, либо не содержащих их совсем. Дисперсия характеризует степень рассеяния точек в пространстве относительно центра кластера. От­дельность характеризует взаимное расположение скоплений точек в пространстве [Там же, 165—166]. Кластеры можно рассматривать как «непрерывные области пространства с относительно высокой плотностью точек, отделенные от других таких же областей облас­тями с относительно низкой плотностью точек» [Там же, 166].

Наиболее известными методами кластерного анализы являются методы одиночной, полной и средней связи, а также метод Уорда [Там же, 191]. Метод Уорда (Ward's method) позволяет создавать кластеры приблизительно равных размеров [Там же, 171]. Он сна­чала объединяет самые близкие объекты, затем к уже образован­ным кластерам присоединяются сходные с ними объекты. Мерой сходства в данном случае является 1 — коэффициент корреляции Пирсона.

На основе анализа содержания переменных, входящих в отдель­ные кластеры, строится группировка респондентов по признакам, включенным в процесс кластеризации. Рассмотрим эту процедуру на примере (рис. 6).

ЕЛЬЦИН
1.2
3.2
зюганов
3.1
4.1
2.2
4.1
ЯВЛИНСКИЙ 2.1
4.3
1.1

0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8

Рис. 6. Дендрограмма мотивов голосования за кандидатов в Президенты России на выборах 1996 г.

Условные обозначения переменных: персональные электоральные предпочтения рес­пондентов на президентских выборах 1996 г. (Ельцин, Зюганов, Явлинский); моти­вация этих предпочтений (1.1. «Он мне нравится», 1.2. «Не хочу перемен», 2.1. «Меня устраивает его программа», 2.2. «Он знает, как решить проблемы страны», 3.1. «Я ему доверяю», 3.2. «Ему нет достойной замены»); мотивация голосования за списки политических партий на парламентских выборах 1995 г. (4.1. «Они заставят правительство думать о народе», 4.2. «Они смогут решить проблемы страны», 4.3. «Устраивает программа партии»). Анализ выполнен с помощью пакета «Statistica» по методу Уорда.

Кластерный анализ основных альтернатив ответа на вопрос о том, за кого намерены голосовать (опрос проводился в мае 1996 г.) респонденты («Ельцин», «Зюганов», «Явлинский»), и вопрос о мо­тивах предстоящего голосования позволили обнаружить особые структуры мотивации электорального выбора у сторонников от­дельных кандидатов в Президенты России на выборах 1996 г. (см.: перечни мотивов в кластерах Ельцина, Зюганова и Явлинского).

Многомерное шкалирование представляет собой процедуру, с помощью которой оценивается степень сходства/различия между переменными. С его помощью мы можем представить набор изу­чаемых переменных в виде скоплений точек (каждой переменной соответствует одна точка). Этот метод позволяет находить в масси­ве данных комплексы сходных друг с другом и отличающихся друг от друга переменных. В геометрическом пространстве сходные переменные (тесно связанные между собой в сознании респонден­тов) располагаются близко друг от друга и образуют скопления точек, отделенные пустым пространством от других скоплений сходных переменных. Чем больше сходства зафиксировано у изучаемых переменных, тем ближе находятся обозначающие их точки на графике. Чем меньше сходства наблюдается у включенных в анализ переменных, тем дальше друг от друга располагаются соот­ветствующие им точки на графике.

Данный метод дает возможность наглядно (на графике) пред­ставить множество переменных и увидеть особенности их конфи­гурации в геометрическом пространстве (чаще всего в двумерном). Подобная процедура используется при сопоставлении значительно­го числа переменных, которое трудно анализировать без визуализа­ции. Перед началом многомерного шкалирования осуществляется процедура преобразования переменных в биноминальные, как и в кластерном анализе.

Рассмотрим пример такой визуализации на основе набора пере­менных, характеризующих идентификацию респондентов с различ­ными взглядами (источник данных тот же, что и в примечании к рис. 6).

На графике рис. 7 видны четыре группы точек, отделенных друг от друга пустым пространством. Эти группы располагаются в рамках двух измерений. Первое измерение основано на противо­поставлении власти и общественности, второе — на противопо­ставлении коммунизма и либерализма. Эти оппозиции наблюда­лись в политическом сознании населения Санкт-Петербурга в конце 2000 г.

Специфическим методом обработки социологической информа­ции является вторичный анализ данных. Он применяется для полу­чения дополнительной информации по уже прошедшему первич­ную обработку массиву данных. Обычно вторичный анализ ис­пользуют при повторной обработке результатов «чужих» или собст­венных исследований. Можно

Коммунистические взгляды Взгляды

Зюганова

КПРФ

Взгляды Путина

Взгляды Яковлева «Яблоко» ОВР

«Единство» Взгляды

Социал-демократические взгляды Явлинского

Либеральные

взгляды

Взгляды Хакамады СПС

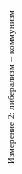0,8

0,6

0,4

0,2

0,0

0,2

0,4

0,6

0,8

4 3 2 1 0 1 2

Измерение 1: власть  общественность

Рис. 7. Конфигурация переменных в пространстве двух измерений² (политическая идентификация и партийные предпочтения на выборах)

выделить два типа вторичного анализа: монографический и сравнительный. В первом случае осу­ществляется повторный анализ одного массива первичных данных, во втором — сопоставляются несколько массивов первичных дан­ных (например, электронные таблицы данных в системе SPSS), полученные отдельными социологическими центрами в разное время, на разных выборках и по различным программам. Разно­типность исследований и используемых в них переменных порож­дает необходимость их стандартизации как условия сопоставимос­ти результатов исследований [Социальные исследования: постро­ение и сравнение показателей. М., 1978. С. 134—139].

Сопоставлять можно лишь однородные переменные, но для обеспечения этой однородности нужно, чтобы сравниваемые пер­вичные данные по этим переменным были получены на однотип­ных выборках, одинаковыми методами и с помощью однотипных шкал. Если у нас нет информации о том, кого и как репрезенти­рует выборка, какие методы были использованы для сбора и ана­лиза данных, как были сформулированы вопросы и какие альтер­нативы предлагались респондентам для ответа на них, то вторич­ный анализ становится невозможным.

Нельзя в строгом смысле слова назвать вторичным анализом часто используемое сопоставление частотных распределений внеш­не сходных переменных, взятых из отчетов по итогам массовых опросов населения, опубликованных в научных изданиях или газе­тах. Как правило, в этом случае авторы не выясняют степень однородности сравниваемых массивов информации, а между тем за каждым числовым значением признака стоит определенное ка­чество. Не выяснив, насколько однородна качественная определен­ность переменных, отобранных из разных массивов данных, мы не можем их сопоставлять.

Для проведения вторичного анализа необходимо изучить описа­ние выполненных исследовательских проектов, по которым имеет­ся первичная информация в существующих отечественных и зару­бежных архивах данных [см., например: Банк социологических данных, 1990 (Информационные ресурсы социологических центров СССР). М., 1990; Международный журнал социальных наук. Май. 1995. № 9. Европейские базы данных по социальным наукам); Мангейм Дж.-Б., Рич Р.-К. Политология. Методы исследования. М., 1997. С. 220—221]. В архивах нужно отобрать необходимые массивы данных, получить разрешение на их использование от ру­ководства соответствующих центров и, сделав с них копии файлов, провести вторичный анализ.

Можно выделить несколько видов сравнительного вторичного анализа: сравнительно-типологический (синхронный), или анализ первичных данных исследований, проведенных в одно и то же время; сравнительно-генетический (диахронный), или анализ ре­зультатов исследований, проведенных в разное время. В любом случае предварительное изучение переменных с целью определения степени их однородности и пригодности для сравнения представ­ляет собой обязательное условие вторичного анализа. Важно отме­тить и то, что в процессе вторичного анализа мы, по существу, мысленно воспроизводим все этапы сопоставляемых исследований и одновременно осуществляем самостоятельное исследование, в ходе которого концептуализируем изучаемую проблему, выдвигаем собственные гипотезы, операционализируем понятия и т.д. Вто­ричный анализ означает новое, дополнительное исследование ста­рых массивов первичных данных.