Взаимосвязь электоральных предпочтений и возраста респондентов

Объединение	Величина	Возраст респондента			Всего
		18—34	35—44	45 и старше
«Единство»	Наблюдаемая частота	61	104	88	253
	Ожидаемая частота	56,0	100,4	96,6	253,0
	Стандартизованный остаток	+0,7	+0,4	0,9
ОВР	Наблюдаемая частота	11	34	17	62
	Ожидаемая частота	13,7	24,6	23,7	62,0
	Стандартизованный остаток	0,7	+ 1,9	1,4
КПРФ	Наблюдаемая частота	6	38	90	134
	Ожидаемая частота	29,7	53,2	51,2	134,0
	Стандартизованный остаток	4,3	2,1	+5,4
СП С	Наблюдаемая частота	53	59	37	149
	Ожидаемая частота	33,0	59,1	56,9	149,0
	Стандартизованный остаток	+3,5	0,0	2,6
«Яблоко»	Наблюдаемая частота	30	82	55	167
	Ожидаемая частота	37,0	66,3	63,8	167,0
	Стандартизованный остаток	1,1	+1,9	1,1

Источник: Опрос населения Санкт-Петербурга, проведенный ЦЭПИ СПбГУ в ноябре 2000 г. Таблица построена с помощью статистического пакета SPSS.

Проверка взаимосвязи отобранных нами переменных по критерию хи-квадрат свидетельствует о ее наличии (наблюдаемое значение критерия хи-квадрат (116,158) выше табличного (45,315) для df = 20 и уровня значимости 0,001). Анализ стандартизованных ос­татков дает более сложную картину. Так, у «Единства» во всех воз­растных группах зафиксированы статистически незначимые вели­чины стандартизованных остатков. На этой основе можно сделать вывод о том, что в данном исследовании связь между возрастом и голосованием за «Единство» не наблюдается. У КПРФ и СПС за­фиксирована диаметрально противоположная картина: в группе от 18 до 34 лет стандартизованные остатки составляют: у КПРФ 4,3, а у СПС +3,5. В группе 45 и старше: +5,4 и 2,6 соответственно. Это означает, что в младшей возрастной группе намного меньше, чем в старшей, тех, кто голосовал за КПРФ, и намного больше тех, кто голосовал за СПС. Голосование за ОВР и «Яблоко» в младшей и старшей возрастных группах характеризуется практи­ческим отсутствием статистически значимых различий. За эти пар­тии в основном голосовали представители средней возрастной группы (величина остатков составляет в обоих случаях +1,9).

Результаты анализа статистических таблиц дают возможность сформулировать гипотезы относительно взаимосвязи признаков изучаемого явления, нуждающихся в дополнительной проверке с помощью статистических методов, о которых пойдет речь далее.

Корреляционный анализ основан на расчете отклонения значений изучаемого признака от линии регрессии (от лат. regressio — воз­врат, в данном случае — возврат к средней) — условной линии, к которой эти значения тяготеют. Чем больше разброс значений, тем слабее связь двух интересующих нас признаков. Чем меньше разброс значений, тем сильнее связь (рис.1).

.. … …..

.. . .. .. .. . .. ….

.. …. .. . . … …. ..

.. ….. . .. . .. …

.. … …..

С ильная прямая связь Слабая прямая связь Отсутствие связи

.. ..

…. ..

….. ..

…… ..

….. ..

.. ..

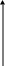
Слабая обратная связь Сильная обратная связь

Рис. 1. Варианты рассеяния значений

Корреляция (от лат. cotrelatio — соотношение) — это статистическая взаимозависимость между признаками изучаемого явления. Корреляционный анализ представляет собой математическую процедуру, с помощью которой изучается эта взаимозависимость. Он заключается в вычислении коэффициентов корреляции — чисел, знак и величина которых характеризуют направление (прямая/обратная) и интенсивность/тесноту (строгая, сильная, умеренная, нулевая) взаимозависимости. Показателем интенсивности связи служит значение коэффициента. Считается, что если он равен 1, то взаимозависимость признаков является строгой (пол­ной); если его значение находится в интервале от 1 до 0,8, то это свидетельствует о сильной их взаимозависимости; если в интервале от 0,7 до 0,3 — об умеренной (неярко выраженной) взаимозависи­мости, а если же оно лежит в интервале от 0,2 до 0,0, то мы имеем дело со слабой или нулевой взаимозависимостью [Кимбл, 174—178; Тюрин и Макаров, 289]. Есть мнение, что в социологических ис­следованиях значения коэффициентов корреляции выше 0,5 встре­чаются не очень часто, поэтому можно принимать во внимание те из них, которые равны или превышают 0,3 [Статистические мето­ды анализа информации..., 97], т. е. характеризуют умеренную вза­имосвязь признаков.

Следует отметить, что коэффициенты корреляции выражают не причинную (обусловленность одного признака другим), а функцио­нальную (взаимная согласованность изменения признаков) зависи­мость между признаками [Рабочая книга социолога, 198]. Различа­ют парную (между двумя признаками) и множественную (между несколькими признаками) корреляции.

Для изучения взаимосвязи признаков, измеренных с помощью различных типов шкал, используются разные коэффициенты кор­реляции. На порядковом уровне измерения признаков наиболее широко применяется коэффициент ранговой корреляции Спирмена, на интервальном уровне обычно используется коэффициент корреляции Пирсона. Коэффициент Спирмена равен +1, когда два ряда проранжированы строго в одном порядке, 1, когда два ряда проранжированы в строго обратном порядке, и равен нулю при полном взаимном беспорядочном расположении рангов.

Коэффициент корреляции Пирсона равен +1 при строгой (пол­ной) прямой взаимозависимости двух признаков (увеличе­ние/уменьшение значений одного признака сопровождается увели­чением/уменьшением значений второго признака). Он равен 1 при строгой (полной) обратной взаимозависимости (увеличе­ние/уменьшение значений одного признака сопровождается уменьшением/увеличением значений второго признака). Наконец, величина этого коэффициента равна нулю при отсутствии взаимозависимости признаков. Об интерпретации значений коэффициентов корреляции, отличных от 1 и 0, говорилось в начале этого параграфа.

В качестве примера корреляционного анализа можно привести статью А. Ослона и Е. Петренко «Факторы электорального поведе­ния: от опросов к моделям» (Вопросы социологии. 1994. № 3. С. 79). Авторы провели анализ связей между голосованием опреде­ленных групп избирателей за разные партии и блоки на базе все­российского опроса ФОМ (декабрь 1993 г.). В данной статье при­водятся значения парных коэффициентов корреляции Пирсона для основных политических партий и блоков (табл. 2).

Таблица 2