IX Ряды.
Обязательный начальный уровень: числовой ряд, сходимость ряда; необходимое условие сходимости; достаточные признаки сходимости для рядов с положительными членами; ряд Дирихле; абсолютная и условная сходимость знакопеременного ряда; признак Лейбница; формулы для радиуса сходимости степенного ряда, интервал сходимости; ряд Тейлора и Маклорена.
Числовые ряды. Основные понятия. Исследование сходимости геометрической прогрессии.
Необходимое условие сходимости. Доказательство расходимости гармонического ряда.
Алгебраических свойства сходящихся рядов. Примеры сходящихся рядов. Достаточные признаки сходимости числовых рядов с неотрицательными членами.
Доказательство предельного признака сравнения.
Знакопеременные ряды. Абсолютная сходимость. Свойства абсолютно сходящихся рядов. Достаточный признак сходимости знакопеременного ряда с доказательством.
Знакочередующиеся ряды. Признак Лейбница. Теорема Римана.
Функциональные ряды общего вида. Область сходимости.
Степенные ряды. Доказательство теоремы Абеля.
Степенные ряды. Область сходимости степенного ряда. Свойства степенных рядов.
Разложение функций в степенные ряды. Представление функции суммой степенного ряда.
Ряд Тейлора. Достаточное условия сходимости. Ряд Маклорена. Получение разложений в ряд Маклорена для функций
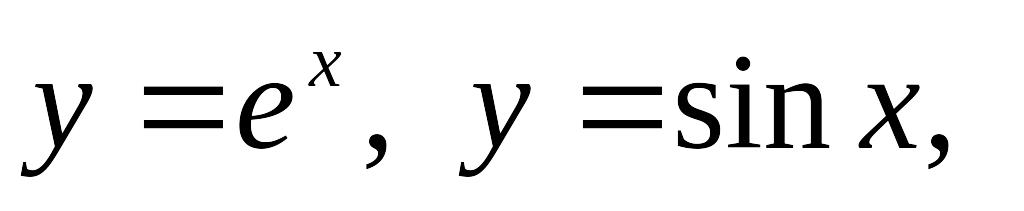
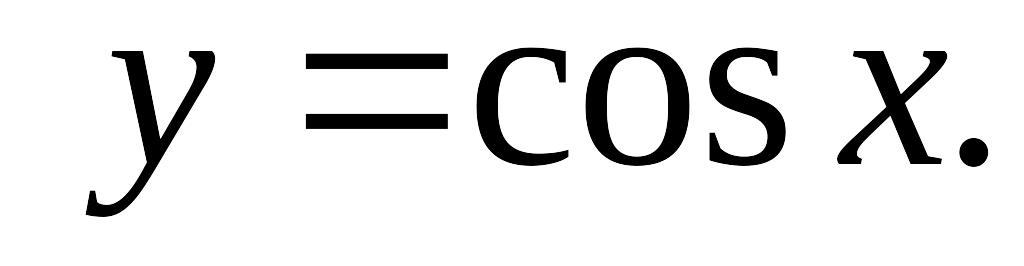
X. Элементы линейной алгебры
Обязательный начальный уровень: матрицы и операции над ними; определитель и его свойства; миноры и алгебраические дополнения; теорема Лапласа; обратная матрица ; решение систем ЛАУ; равные векторы; уметь строить сумму и разность векторов; условия коллинеарности и ортогональности двух ненулевых векторов; скалярное произведение векторов; собственные числа и собственные векторы матрицы. линейная зависимость (независимость) системы векторов; базис, ранг системы векторов.
89. Геометрическое толкование вектора. Линейные операции. Алгебраическое описание вектора.
Скалярное произведение векторов. Доказательство критерия ортогональности.
Виды матриц. Операции над матрицами. Матричные уравнения и способы их решения.
Определители. Свойства и методы нахождения. Теоремы Лапласа и аннулирования.
Обратная матрица. Доказательство единственности. Свойства А-1.
Системы ЛАУ. Метод Гаусса. Прямой ход. Обратный ход.
Системы с невырожденной квадратной матрицей и способы их решения.
Линейная зависимость. Утверждения о линейной зависимости системы векторов.
Линейная независимость. Утверждения о линейной независимости.
Доказательство теоремы о линейной независимости диагональной системы. Система единичных векторов. Утверждений о системе единичных векторов.
Базис и ранг системы векторов и векторного пространства . Доказательство теоремы о базисе.
Ортогональная система векторов. Доказательство теоремы о базисе евклидова пространства.
Вывод формулы для координат вектора в ортонормированном базисе.
Ранг матрицы. Свойства ранга.
Системы ЛАУ. Критерий совместности Кронекера-Капелли. Однородные системы ЛАУ. Доказательство теоремы о ненулевом решении однородной системы.
Собственные векторы и собственные значения матрицы. Доказательство единственности собственного значения.
Составитель: доцент кафедры __________________/_Е. А.Сетько
Заведующий кафедрой __________________/_Ю.М. Вувуникян