VII Функции двух переменных
Обязательный начальный уровень: функция двух переменных; определение предела функции по Коши и по Гейне; ББ и БМ функции двух переменных; непрерывность функции в точке; частные производные, их геометрический и физический смысл; дифференцируемость; дифференциал; локальный экстремум функции двух переменных; необходимое условие локального экстремума; достаточное условие локального экстремума; седловые точки.
Функции двух переменных. Область определения, множество значений, график. Примеры. Линии уровня, их графическая интерпретация, примеры и применение.
Предел функции в точке по Гейне. Исследование существования пределов:
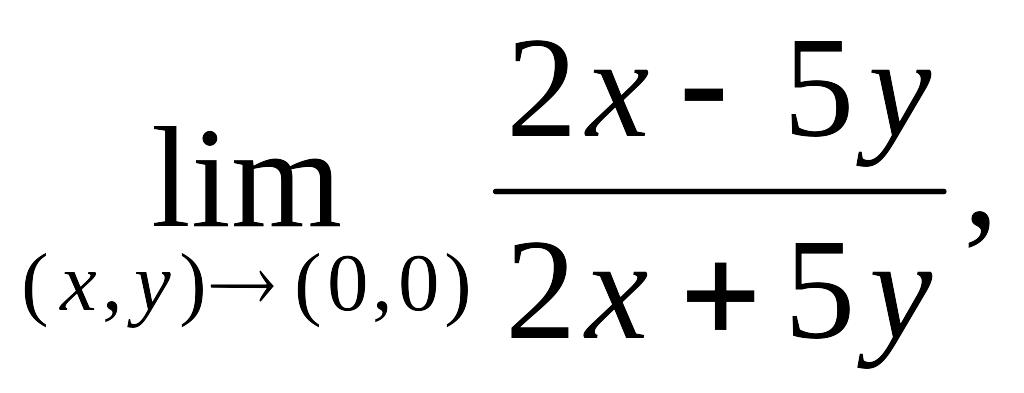
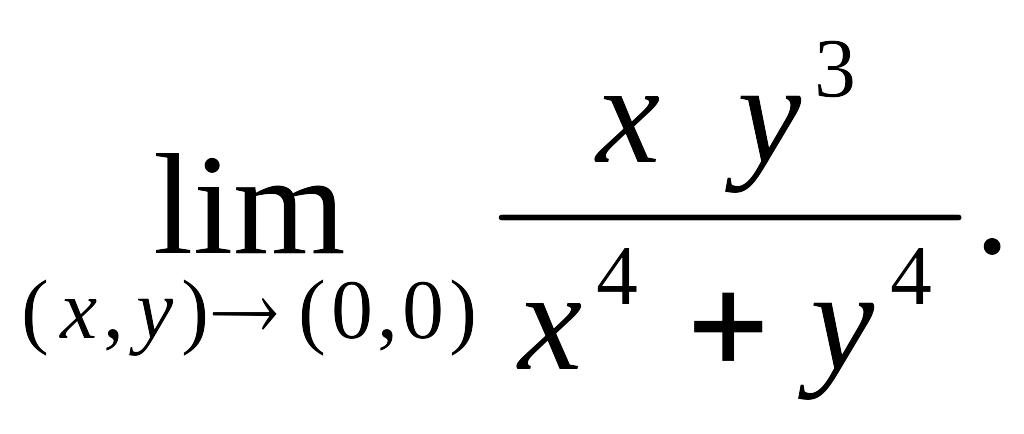Предел
функции по Коши, геометрический смысл
предела и его свойства. ББ и БМ функции
двух переменных и их свойства.Непрерывность функции в точке (различные формы определения). Непрерывность по одной из переменных и непрерывность по совокупности переменных. Алгебраические свойства непрерывных функции двух переменных. Точки разрыва. Примеры.
Частные производные функции двух переменных, их геометрический и физический смысл. Частные производные высших порядков. Теорема о смешанных частных производных.
Дифференцируемость функции двух переменных в точке. Доказательство двух необходимых условий дифференцируемости. Иллюстрация того, что необходимые условия не являются достаточными. Достаточное условие дифференцируемости.
Дифференциал функции двух переменных. Получение формулы для нахождения дифференциала. Применение дифференциала в приближенных вычислениях. Доказательство теоремы о производной сложной функции.
Производная по направлению. Вывод формулы. Градиент функции. Теорема о градиенте.
Локальный экстремум функции. Доказательство необходимого условия локального экстремума. Критические точки. Седловые точки. Примеры.
Достаточное условие локального экстремума. Исследование случая
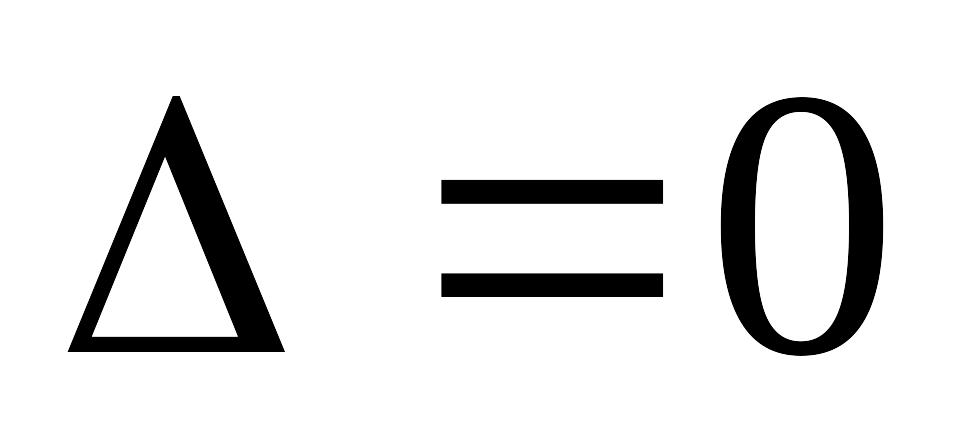.Выпуклые множества и выпуклые функции. Особенности экстремума для выпуклых функций. Глобальный экстремум. Нахождение наибольшего и наименьшего значения функции в области.
Условный экстремум. Функция Лагранжа.
VIII Дифференциальные уравнения.
Обязательный начальный уровень: определение дифференциального уравнения, его решение, общее решение, частное решение, задача Коши; метод Эйлера нахождения общего решения однородного дифференциального уравнения 2-го порядка; неоднородного уравнения со специальной правой частью.
Дифференциальные уравнения 1-го порядка. Решение дифференциального уравнения, задача Коши, общее решение, частное решение, особое решение. Теорема Коши.
Виды дифференциальных уравнений 1-го порядка и способы их решения. Математическая модель рекламы с решением дифференциального уравнения.
Дифференциальные уравнения 2-го порядка. Основные понятия. Теорема Коши.
Однородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Свойство частного решения. Построение общего решения. Метод Эйлера.
Решение неоднородного дифференциального уравнения.