III. Критерий Сэвиджа.

1. Находим лучшие результаты каждого в отдельности столбца, т.е. maxX_ij. Таковыми в нашем примере будут для первого столбца 16, для второго – 12, для третьего – 6. Это те же максимумы, которые можно было получить, если бы удалось точно угадать возможные реакции рынка.

2. Определяем отклонения от лучших результатов в пределах каждого отдельного столбца, т.е. maxX_ij – X_ij. Получаем матрицу отклонений, которую можно назвать матрицей сожалений, ибо ее элементы – это недополученная прибыль от неудачно принятых решений из-за ошибочной оценки возможной реакции рынка. Матрицу сожалений можно оформить в виде табл. П.4.6.

Таблица П.4.6

Матрица сожалений

Вариант решения о переходе к массовому производству	Возможные размеры упущенной прибыли в условиях, когда массовый спрос возникнет
	немедленно	через 1 год	через 2 года
Перейти немедленно	0	6	12
Перейти через 1 год	11	0	4
Перейти через 2 года	16	10	0

Судя по приведенной матрице, не придется ни о чем жалеть, если фирма немедленно перейдет к массовому выпуску новой продукции и рынок сразу отреагирует массовым спросом. Однако если массовый спрос возникнет только через 2 года, то придется пожалеть о потерянных вследствие такой поспешности 12 млн у.е., и т.д.

3. Для каждого варианта решения, т.е. для каждой строки матрицы сожалений находим наибольшую величину. Получаем столбец максимумов сожалений в виде табл. П.4.7.

4. Выбираем то решение, при котором максимальное сожаление будет меньше других. В приведенном столбце максимальных сожалений оно стоит во второй строке, что предписывает перейти к массовому выпуску через год.

Таблица П.4.7

Максимальные сожаления

Вариант решения о переходе к массовому производству	Столбец максимальных сожалений
Перейти немедленно	12
Перейти через 1 год	11
Перейти через 2 года	16

IV. Критерий пессимизма-оптимизма Гурвица.

Для условий нашего примера, придав па­раметру k значение на уровне 0,6:

Н₁ = 16 · 0,6 + (–6) · 0,4 = 7,2;

Н₂ = 12 · 0,6 + 2 · 0,4 = 8;

Н₃ = 6 · 0,6 + 0 · 0,4 = 3,6.

Исходя из максимума значения данного критерия, надо принять решение о переходе к массовому выпуску новой продукции через год.

В нашем примере стратегия А₂ (см. табл. 3.5) фигурирует как оптимальная по трем крите­риям выбора из четырех испытанных, степень ее надежности можно признать достаточно высокой для того, чтобы рекомендовать эту стратегию к практическому применению. Дей­ствительно, в нашем примере при таком решении не придется особенно сожалеть об упу­щенной прибыли и не придется ожидать больших убытков, т. е. сразу минимизируются и сожаления об упущенной прибыли, и возможные убытки.

Критерии принятия решений в условиях риска.

1. Критерий математического ожидания

Таблица П.4.7

Таблица выплат для критерия математического ожидания

Вариант решения о переходе к массовому производству	Размер выплат (млн у.е.) при возможных сроках и вероятностях возникновения массового спроса
	немедленно (0,2)	через 1 год (0,5)	через 2 года (0,3)
Перейти немедленно	16	6	-6
Перейти через 1 год	5	12	2
Перейти через 2 года	0	2	6

Для каждой строки, т.е. для каждого варианта решения, находим математическое ожидание выплаты:

М₁ = 16 · 0,2 + 6 · 0,5 – 6 · 0,3 = 4,4;

М₂ = 5 · 0,2 + 12 · 0,5 + 2 · 0,3 = 7,6;

М₃ = 0 + 2 · 0,5 + 6 · 0,3 = 2,8.

Максимальным из них является математическое ожидание второй строки, что соответствует решению начать массовый выпуск новой продукции через год.

2. Критерий Лапласа.

Суммы выплат для отдельных вариантов решений в нашем примере составят:

∑X_1j = 16; ∑X_2j = 19; ∑X_3j = 8.

Наибольшей является сумма выплат во второй строке табл. П.4.7. Значит, в качестве оптимального решения надо принять переход на массовый выпуск продукции через год, т.е. то же решение, что было признано с помощью критерия математического ожидания.

Пример 4. Принятие решений с помощью «дерева решений»

Необходимо выбрать лучший из трех возможных инвестиционных проектов: ИП₁, ИП₂, ИП₃.

Допустим, что проекты требуют вложения средств в размерах 200, 300 и 500 млн руб. и могут дать прибыль в размерах 100, 200 и 300 млн руб.

Риск потери средств по этим проектам характеризуется вероятностями на уровне 10 %, 5 % и 20 % соответственно.

Какой проект лучше?

Решение.

Найти ответ с помощью чисто математических средств трудно. С помощью же «дерева решений» задача легко решается. «Дерево решений» для условий данного примера пред­ставлено на рис. П.4.1.

После составления «дерева решений» начинается его обратный анализ. Идя по «дере­ву» справа налево и попадая в кружки, мы должны поставить в них математические ожи­дания выплат. Расчет последних выглядит так:

М(х₁) = 100 · 0,9 – 200 · 0,1 = 70;

М(х₂) = 200 · 0,95 – 300 · 0,05 = 175;

М(х₃) = 300 · 0,8 – 500 · 0,2 = 140.

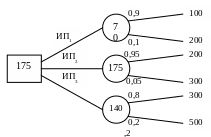
Рис. П.4.1 Пример составления дерева решений

Эти математические ожидания поставлены в кружки, изображающие узлы возникно­вения неопределенностей.

Двигаясь налево, мы попадаем в квадрат и обязаны поставить в него максимальную величину из тех, что стоят на концах выходящих из него ветвей. В нашем случае опти­мальным является решение вложить средства в ИП₂.

ПРИЛОЖЕНИЕ 5