2.2. Вычисление внутренних усилий и построение их эпюр

В сечении определяют центр приведения и показывают внутренние усилия. Записывают условия равновесия для отсеченной части тела:

Из этих условий при подробном вычислении их левых частей вытекают уравнения, в которых неизвестные внутренние усилия выступают в явной форме. Совпадение числа уравнений с числом неизвестных внутренних усилий означает, что нахождение последних − статически определимая задача. Записав, например, уравнение равновесия для левой части (рис.2.1,в) получаем Таким образом, поперечную силу в сечении можно определить как алгебраическую сумму проекций на ось у внешних сил, приложенных к рассматриваемой части. Эти силы входят в уравнение со знаками, определенными для внутренних сил. Аналогичный алгоритм можно составить для других внутренних сил. Иллюстрацией сказанному служит пример 2.1 в п.2.4.

Проверка правильности определения усилий ведется в двух направлениях: а) выполнение условий равновесия, не использованных при определении внутренних усилий; б) проверка равновесия части тела, которая не рассматривалась при решении задачи.

Эпюра внутреннего усилия обычно строится по точкам с помощью его аналитического выражения. В случае прерывного характера распределения нагрузки, а также прерывности координат сечения и координат центра приведения требуется записать аналитические выражения для отдельных участков.

Усилия могут быть определены более просто, если удается уменьшить число искомых неизвестных (использование условий прямой и обратной симметрии, разложение пространственной системы сил на несколько плоских систем, использование известных частных решений) или путем разделения вхо-

дящих в уравнения неизвестных (например, путем рационального выбора осей проекций и моментов).

Прямосимметричные внутренние усилия (продольная сила, изгибающие моменты) перемещают части тела в симметричные положения, обратносим-метричные внутренние усилия (поперечные силы, крутящий момент) − в обратносимметричные положения. В сечении, по обе стороны от которого нагрузка прямосимметрична, обратносимметричные усилия обращаются в нуль (и наоборот).

2.3. Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими , и интенсивностью моментов с составляющими . Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.2.3) составим дифференциальные уравнения равновесия.

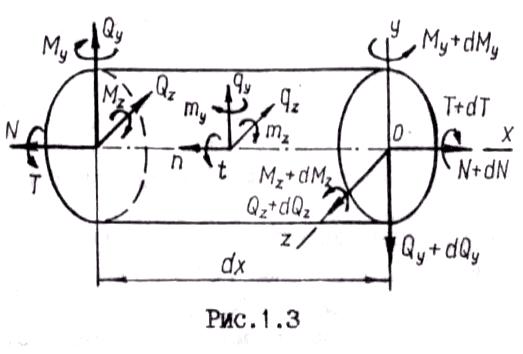
Рис. 2.3

Из условий следуют уравнения:

Из условий получаем:

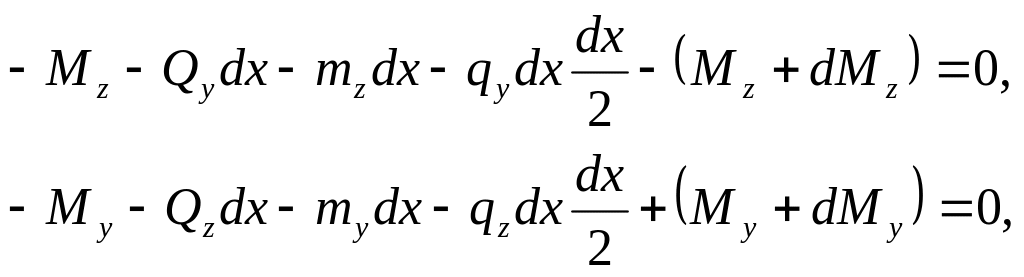
откуда, пренебрегая бесконечно малыми второго порядка, находим

Подставляя выражения в соответствующие дифференциальные уравнения, получаем

Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

Постоянные интегрирования С_i (i=1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре определить характер эпюры . В частности, на участках, где =0 ( =0), т.е. при соблюдении зависимостей

можно установить, что при М_z = const имеем Q_y = 0 (при М_y = const имеем Q_z = 0). Переменная величина достигает экстремальных значений в точках, где Q_y = 0 (Q_z = 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью.