2. Внутренние силы

1. Метод сечений

Внутренние силы возникают между отдельными элементами сооружения и между отдельными частями элемента под действием внешних сил. Определение внутренних сил производят методом сечений. Сущность его заключается в том, что тело, находящееся в равновесии (рис.2.1,а), рассекают мысленно на две части (рис.2.1,б), отбрасывают одну из частей, заменяя влияние отброшенной части внутренними силами, и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние силы¹ и подлежащие определению внутренние силы, распределенные по сечению.

а

б

в

Рис. 2.1

Обычно плоскость сечения проводится перпендикулярно касательной к оси бруса. Систему внутренних сил можно привести к одной силе R и к одной паре М. Выберем в качестве центра приведения сил центр тяжести сечения 0 и

направим ось Оx правой прямоугольной системы координат перпендикулярно сечению в сторону внешней нормали. Разложим векторы R и M на составляющие (рис. 2.1,в). Силу N , направленную по касательной к оси стержня, называют продольной силой. Силы Q_y и Q_z, направленные по нормали к оси стержня, называют поперечными силами. Момент Т относительно оси х называют крутящим. Моменты М_y и M_z носят название изгибающих. Эти шесть внутренних усилий могут быть найдены из шести уравнений равновесия тела в пространстве, составленных для рассматриваемой части бруса. Уравнения составляются применительно к недеформированному телу, если наблюдаются малые изменения его размеров и формы. Принятие такого допущения значительно упрощает задачу, уравнения становятся линейными, что позволяет пользоваться принципом независимости действия сил (принципом наложения). Последний гласит, что результат совместного воздействия на тело системы сил равен сумме частных результатов воздействия каждой силы в отдельности.

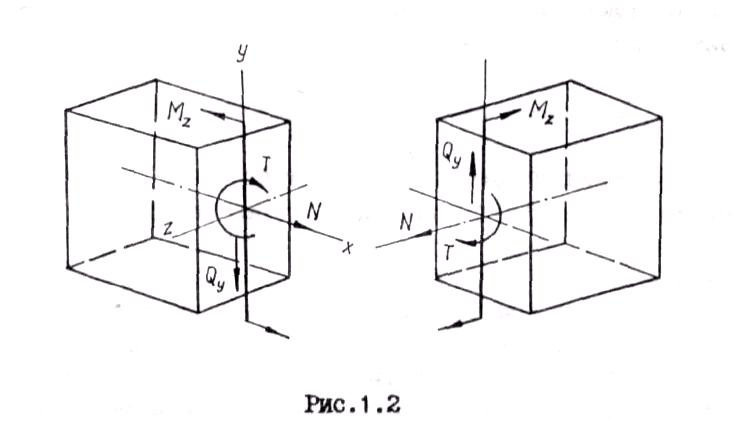
Рис. 2.2

Каждому из внутренних усилий соответствует свой вид деформирования тела: N − растяжение (сжатие), Q_y и Q_z − сдвиг, Т − кручение, М_у и М_z − изгиб. Эти деформации, как правило, возникают в различных сочетаниях. Продольная сила считается положительной, если ее направление совпадает с направлением внешней нормали к сечению. Крутящий момент принимается положительным, если при взгляде в торец отсеченной части бруса со стороны его внешней нормали он представляется направленным по ходу часовой стрелки. Изгибающий момент считается положительным, когда на левом торцe правой части бруса он направлен по ходу часовой стрелки, а на правом торце левой части − против хода часовой стрелки. Поперечная сила положительна, если она стремится вращать отсеченную часть бруса (на которую она действует) по ходу часовой стрелки относительно любой точки на внутренней нормали к сечению. Положительные знаки усилий показаны на рис.2.2.

При определении знаков внутренних усилий в вертикальных брусьях необходимо какой-то конец бруса (нижний или верхний) принимать в качестве левого и отмечать его на чертеже каким-либо значком.

Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой. Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.