12.2. Определение перемещений методом Мора

При использовании этого метода (в литературе его называют: методом возможной работы; методом фиктивной нагрузки; методом единичной нагруз-ки) необходимо рассматривать две системы нагрузок, действующих на кон-струкцию. Первая система включает все реальные нагрузки, а вторая система включает только единичную нагрузку, которая действует на конструкцию. Еди-ничная нагрузка представляет собой фиктивную или искусственно введённую нагрузку, которая позволяет определить перемещение конструкции при действии реальных нагрузок. Единичная нагрузка прикладывается в той точке конструкции перемещение которой определяем и действует в направлении ис-комого перемещения. Если определяется линейное перемещение, то прикладывает единичную силу, а если угловое - единицу момента сил.

Действующая на конструкцию единичная нагрузка, которая представляет собой вторую систему нагрузок, вызывает возникновение реакций опор и внут-ренних усилий, которые обозначим через Вместе с единичной наг-рузкой и реакциями опор они образуют систему сил, которая находится в рав-новесии. Если конструкции предать малую возможную деформацию, в качест-ве которой возьмем действительные деформации конструкции, создаваемые пе-

рвой системой нагрузок, то возможная работа внешних сил будет представлять

собой только работу, совершаемую самой единичной нагрузкой. Эта возмож-ная (виртуальная) работа равна произведению единичной нагрузки на переме-щение которое совершает точка её приложения; таким образом:

А_внш=1

Где величина представляет собой искомое перемещение точки конструкции за счёт реальной нагрузки.

Возможная работа внутренних сил представляет собой работу, совершае-мую этими силами ( ) при возможной деформации элементов конс-трукции. Эти деформации выбираем такими же, как и действительные дефор-

мации, возникающие при действии на конструкцию реальных нагрузок. Обоз-начая эти деформации через и (рис. 12.2 при растяжении (а), из-гибе (б), сдвиге(в), кручении (г)), получим следующие выражения для работы внутренних сил:

И_внт=∫ +∫ +∫ +∫

Рис. 12.2

Приравняв, выражение для работ внешних и внутренних сил получаем:

=∫ +∫ +∫ +∫

Если деформации малые упругие (справедлив закон Гука), а внутренние усилия в первой системе реальных нагрузок обозначить через N_F, M_F, Q_F и T_F, то деформации элемента можно записать:

Первое из этих выражений даёт удлинения элемента при действии нормальной силы N_F, а последующие деформации при изгибе, сдвиге и круче-нии.

В окончательном виде метод Мора имеет вид

Входящий в формулу К- числовой коэффициент, зависящий от формы поперечного сечения бруса.

Порядок определения перемещений можно кратко изложить следующим образом:

1) разделив конструкцию на участки записываем аналитические выраже-ния для внутренних силовых факторов, на каждом участке, вызванных систе-мой реальных нагрузок- N_F, M_F, Q_F, T_F;

2) в точке, перемещение которой хотим определить, в направлении иско-мого перемещения приложим единичную нагрузку и определяем внутренние силовые факторы, возникающие в поперечных сечениях, только от этой едини-чной нагрузки (и возникших реакций). При этом необходимо, чтобы правила знаков и направление обхода участков в п.п 1и 2 были бы те же самые.

3) подставить найденные значения в интегралы Мора и выполнить инте-грирование по всей конструкции и просуммировать результаты для получения величины перемещения Если результат получен со знаком “минус”, то это означает, что направление искомого перемещения противоположно направле-нию единичной нагрузки.

Не все члены интегралов Мора могут понадобиться. Так при расчёте ферм только слагаемые, содержащие нормальные силы необходимо учитывать, а для балки или плоской рамы существенными будут только деформации изги-ба и уравнение упрощается:

Такие интегралы можно вычислить для каждого элемента конструкции (участка), а затем просуммировать полученные результаты.

При вычислении интеграла Мора, как правило, рассматриваются такие элементы конструкций в которых жёсткости (EA, EJ, GJ_р) остаются постоянны-ми. Следовательно их можно вынести из под интегралов, после чего все подин-тегральные члены уравнения имеют форму произведений, скажем:

∫ М_F dx.

В 1925 г. студент Московского института железнодорожного транспорта А.Н. Верещагин предложил упрощение вычислений с использованием форму-лы Мора для стержневых систем, состоящих из прямых участков с постоянной (в пределах каждого участка) жёсткостью. Упрощение базируется на том, что эпюры от единичных нагрузок оказываются линейными.

Допустим, на участке длинной l нужно взять интеграл.

J=

при условии, что f₂(x)- линей-ная функция.

f₂(x)=b+kx.

Тогда:

J=

П ервый из интегралов предста-вляет собой площадь, ограни-ченную кривой f₁(x) (рис. 12.3 а), которую обозначим Вто-рой интеграл представляет со-бой статический момент этой площади относительно оси y, т.е.

где х_с- координата центра тяже-

Рис. 12.3 сти первой эпюры.

Итак, J= Так как b+kx_c=f₂(x_c) (рис. 12.3 б), то

J=

Операция интегрирования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

В стречающиеся на практике эпюры могут быть расслоены на простей-шие фигуры: прямоугольник, треугольник, параболу, для которых величина площади и положение центра тяжести (рис. 12.4) известны.

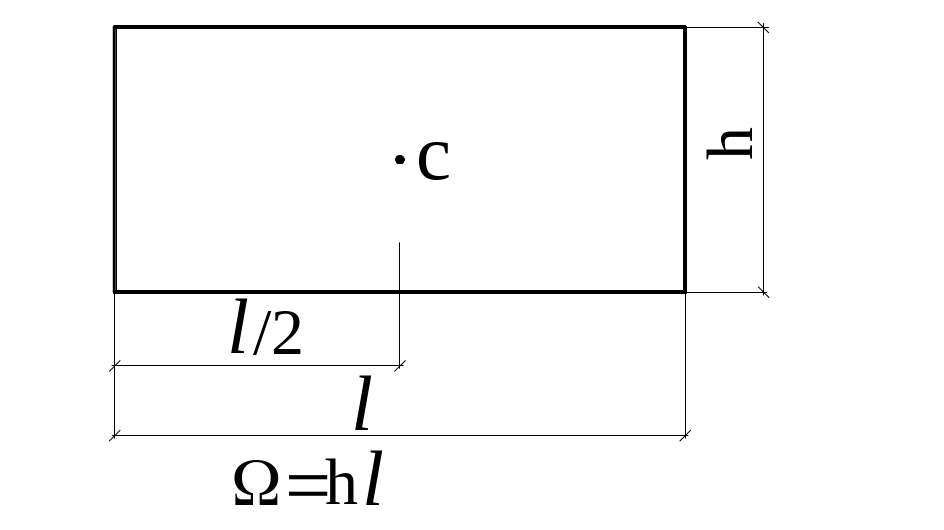
Рис.12.4

Определение перемещений от симметричного и обратно симметричного воздействия надо вести раздельно, проводя вычисления только для половины

системы. Из свойства её симметрии вытекает важное правило: если при “перем-

ножении” эпюр одна из них симметрична, а другая обратно симметрична, то их “ произведение”(премещение)равно нулю.

Если жёсткость стержня переменная, то эпюру усилий от внешних воз-действий надо привести к одной жёсткости, умножая её ординаты , где J_o- момент инерции одного из сечений.