4.3. Перемещения и деформации

Твердое тело, как правило, закреплено. В таком случае пе­ремещение точки тела вызывается только его деформированием. Это перемещение характеризуется вектором с проекциями u, v, w на оси x, у, z, являющимися функциями координат: u = u(x, у, z), v = v(x, у, z), w = w(x, у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x, у, z непрерывны, кроме, возможно, особых точек, линий или поверхно­стей.

Элементарный параллелепипед, вырезанный в окрестности ка­кой-либо точки, деформируется таким образом, что изменяется длина его ребер и искажаются первоначально прямые углы между гранями, т.е. изменяются объем и форма.

Д ля определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ. После деформирования те­ла он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆l'. Исходя из незначи­тельного изменения геометри­ческих характеристик тела в результате деформирования, можно считать Рис. 4.4

угловое пере­мещение (угол поворота) ∆α малым по сравнению с единицей, так что cos∆α ≈ 1. Величина ∆λ = ∆l' – ∆l представляет со­бой абсолютное изменение первоначальной длины отрезка АВ. Ве­личина ∆λ/∆l есть средняя линейная деформация вдоль оси n в точке А.

Уменьшая размеры отрезка, в пределе получаем

Безразмерная величина ε_n есть истинная линейная деформация вдоль оси n в точке А.

Полагая, что λ − непрерывная функция l, получим

ε_n = ∂ λ /∂l.

Если λ зависит от одной переменной l, то

ε_n = dλ /dl.

Для определения деформации сдвига в точке А в плоскости mn возьмем на этой плоскости два малых отрезка АВ и АС, пересекающихся в точке А под углом 90°. После деформирования тела они обратятся в отрезки А'В' и А'С' с

иным углом пересечения и расположатся в другой плоскости m'n', составляющей с первоначальной угол ∆α. Принимая, как и раньше, cos∆α ≈ 1, определим деформацию сдвига как разность величин углов В'А'С' и ВАС. Наложим угол В'А'С' на угол ВАС (рис.4.5) и установим углы поворота отрезков относительно своих первоначальных положений – α₁ и α₂. Величина α₁ + α₂ = γ_mn и есть деформация сдвига в точке А в плоскости mn.

П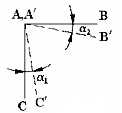 оложительными принимают линей­ную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первона­чального угла пересечения отрезков.

Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с едини-цей, а также их высокими сте­пенями по сравнению с первой степенью.

Рис. 4.5 Деформированное состояние в точке – состояние тела в ок­рестности данной точки, определяемое совокупностью деформаций всех линейных элементов, проходящих через данную точку. В слу­чае малых деформаций оно полностью определяется линейными де­формациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть незави­симых скалярных величин определяют тензор деформаций:

З десь (при γ_yx=γ_xy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированно­го параллелепипе-да, что видно, например, из рис. 4.6 (в плоско­сти xy).

Рис. 4.6

Главные оси деформации – три взаимно перпендикулярные прямые, прохо-дящие через данную точку тела и совпадающие по направлениям с такими тре-мялинейными элементами тела, которые остаются взаимно перпендикулярны-ми и после деформации. Линейные деформации по направлениям этих осей на-

зываются главными деформациями и обозначаются ε₁, ε₂, ε₃ (ε₁ ≥ ε₂ ≥ ε₃).

Кинематические граничные условия на части поверхности тела с заданным вектором перемещений имеют вид