3.5. Практикум

Примеры

1. Определить положение главных центральных осей и величину главных центральных моментов инерции для составного сечения (рис.3.8). Построить эллипс инерции.

Решение. Центр тяжести фигуры лежит на оси симметрии у, которая и является главной центральной осью.

Выбираем произвольную ось z' и определяем ординату центра тяжести, предварительно разбив сечение на два прямоугольника:

Через точку С перпендикулярно оси у проводим ось z, которая и будет другой главной центральной осью.

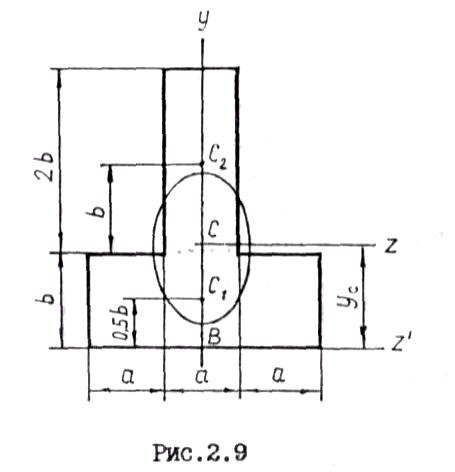
Рис. 3.8

Для каждого из прямоугольников находим моменты инерции относительно их главных центральных осей:

а также расстояния их центров тяжести от оси z:

Используя зависимости между моментами инерции относительно парал-лельных осей, находим величины главных центральных моментов инерции:

Определяем радиусы инерции:

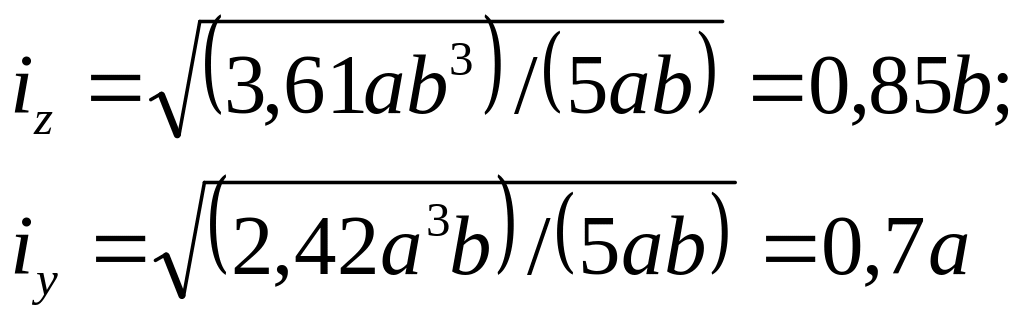
и строим эллипс инерции (см.рис.3.8), отложив величины i_z и i_y на перпендику-лярах к соответствующим осям.

2. Найти расстояние с между ветвями составного стержня, обеспечивающее равенство главных моментов инерции сечения (рис.3.9).

Решение. Требуемое условие обеспечивается равенством моментов инерции относительно осей симметрии z и у, являющихся главными центральными осями сечения.

Разбиваем каждую часть сечения на три прямоугольника, как показано на рис.3.9, и определяем моменты инерции:

Рис. 3.9

Приравнивая I_y и I_z, получаем уравнение

или

откуда с = 4,19 см.

Здесь и отрицательный корень с = –13,73 см имеет смысл. Читателю предлагается изобразить составное сечение для этого случая.

Вопросы для повторения

1. Что называется статическим моментом сечения?

2. Какую размерность имеет статический момент сечения?

3. Как определяют координаты центра тяжести сложного сечения?

4. Что называют осевыми, центробежными, полярными моментами инерции сечения?

5. Размерность моментов инерции сечения?

6. Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

7. От чего зависит знак центробежного момента инерции сечения?

8. Какие оси называют главными осями инерции?

9. Что такое главные центральные оси инерции и почему необходимо вы-числять значения главных моментов инерции относительно главных централь-ных осей?

10. Как определяют главные моменты инерции и положение главных осей?

11. Чему равен центробежный момент инерции относительно главных осей инерции?

12. Какие центральные оси являются главными у сечений, имеющих более двух осей симметрии?

13. Почему производят разбивку сложного сечения на составляющие простые части при определении статических моментов и моментов инерции сечения?

14. Дайте определение радиуса инерции?

Тесты для повторения

1. Статический момент площади сечения относительно центральной оси “Υ”

(а) S_y > 0; (б) S_y < 0; (в) S_y = 0; (г) S_y 0.

Ответ: (в), потому что признаком того, что из семейства параллельных осей ось, относительно которой статический момент равен нулю, является цент-ральной.

2 . Для какой из осей статический момент сечения S будет наибольшим:

(а) – у; (б) - х₁; (в) - х₂; (г) -х₃.

Ответ: (г) так как S_х > S_y поскольку элементарные площадки удалены на расстояния, большие чем от оси “у”, а из осей х₁, х₂, х₃ статический момент имеет большую величину для наиболее удалённой оси.

3. Если J_y=J_z , а D _yz=0, то оси “y”,”z” являются:

(а) центральными; (б) главными центральными;

(в) осями симметрии; (г) главными.

Ответ: (г), потому что равенство центробежного момента инерции нулю – необходимое и достаточное условие для главных осей инер-ции. Если оси “y”,”z” были бы центральными, то необходимо в дополнение что бы S_y=0 и S_z=0.

4. При повороте взаимно перпендикулярных осей “y”и”z” относительно общего начала координат сумма осевых моментов инерции (J_y+J_z):

(а) зависит от угла поворота; (б) не изменяется;

(в) равна нулю; (г)изменяется, но не зависит от угла поворота.

Ответ: (б) сумма осевых моментов относительно двух ортогональных осей при их повороте остаётся постоянной величиной, равной полярному моменту инерции J_р= ρ² dA.

5. Ось “y” изменила своё направление на противоположное. Значение какого момента инерции изменится:

(а) J_y; (б) J_z; (в) D_yz; (г) J_p;

О твет: (в), величина центробежного момента сохранится, но знак изменится на противоположный. Для других моментов инерции “x”,”y”, координаты стоят под интегралом в квадрате, следовательно будет координата “+y” или ”-у” – величина момента не изменится.

6. Осевой момент инерции для треугольника будет максимальным для:

(а) z₀; (б) z₁; (в) z₂; (г) z₃;

Ответ: (г), поскольку наименьшее значение осевой момент J_z имеет для центральной оси z₀, а значение осевого момента инерции для оси, параллельной цен-тральной возрастает на величину равную произведе-

нию площади фигуры на квадрат расстояния между осями.