МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Управление и информатика в технических системах»

В.Г.Сидоренко

Е.П. Балакина

Н.Н. Зольникова

СПОСОБЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

Методические указания

к лабораторным работам

Москва – 2009

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Управление и информатика в технических системах»

В.Г.Сидоренко

Е.П. Балакина

Н.Н. Зольникова

СПОСОБЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

Рекомендовано редакционно-издательским

советом университета в качестве методических указаний

для студентов специальностей

«Управление и информатика в технических системах» и «Компьютерная безопасность»

Москва – 2009

УДК 004

С34

Сидоренко В.Г., Балакина Е.П., Зольникова Н.Н. Способы цифровой обработки сигналов. Методические указания. - М.: МИИТ, 2009. – 38 с.

В методических указаниях описаны лабораторные работы, посвященные оцифровке и восстановлению сигналов с применением пакета Mathcad, изучению спектрального анализа звука различных музыкальных инструментов, и обработке изображений с использование системы MathLab.

Предназначено для студентов специальностей «Управление и информатика в технических системах» и «Компьютерная безопасность».

©Московский государственный

университет путей сообщения

(МИИТ), 2009

Лабораторная работа №1. Оцифровка и восстановление сигнала

Цель лабораторной работы: Научиться оцифровывать и восстанавливать радиоимпульс с заданными параметрами.

Задание на лабораторную работу:

1. Смоделировать радиоимпульс с огибающей и параметрами согласно номеру варианта.

2. Получить цифровой сигнал.

3. Вычислить ошибку квантования.

4. Восстановить сигнал по его цифровому представлению.

5. Сравнить результаты для разных частот дискретизации и разном количестве уровней квантования и сделать соответствующие выводы.

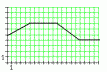
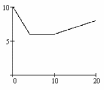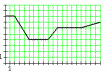
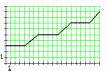
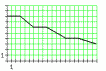
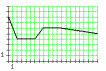
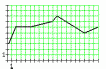
П ример.: Смоделировать радиоимпульс с огибающей, представлен-ной на рисунке, затем оцифровать его и полученный цифровой сигнал восстановить. Длительность импульса Т = 20 Мс, частота несущей  = 0.7 кГц, частота дискре-тизации d = 57 кГц, количество уровней квантования n = 8.

Порядок выполнения (вычисления реализованы в пакете MathCad):

1. Моделирование радиоимпульса.

Задается информационный сигнал 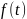. Добавление нового уровня реализуется оператором Add line в меню Programming. Знаки логических операций находятся в меню Boolean. Для перехода между уровнями вводимой информации используется клавиша пробел. Знак := является операцией присвоения значения переменной. Объявлять переменные необходимо до их непосредственного использования в вычислениях.

.

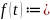Затем последовательно вводятся время наблюдения T, частота несущей 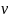и рассчитывается частота ω.

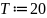
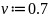
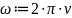
Модулированный сигнал определяется как:

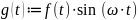
Затем строится график функции. Для этого в панели инструментов Graph выбирается плоский график. Появляется окно построения графика, в котором необходимо ввести отображаемые функции, разделяя их между собой запятыми; аргумент функции; минимальное и максимальное значение для аргумента; минимальное и максимальное отображаемое значение для оси ординат. При вводе аргумента функции необходимо учитывать, что в случае, если аргумент одинаков для всех отображаемых функций, его достаточно указать один раз, в противном случае последовательно указываются аргументы для каждой функции из списка отображаемых и разделяются между собой запятыми. После этого Mathcad выполнит построение функции в формате по умолчанию. Для изменения формата необходимо дважды щелкнуть мышью по области графика. В появившемся окне выбирается пункт Crossed для правильного отображения осей координат и Grid line для отображения промежуточных делений.

2. Дискретизация радиоимпульса.

Задается частота и рассчитывается период дискретизации

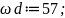
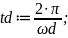
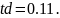
Задается начальная точка, относительно которой осуществляется дискретизация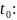

.

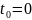Определяется число отсчетов N. Число отчетов должно быть целым числом, для этого используется функцию округления Round:

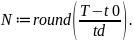
Номер отсчета изменяется в пределах от 0 до N:

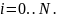
Далее определяется значение аргумента для i-го отсчета

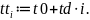
Тогда дискретный сигнал определяется как

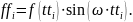
Затем на графике осуществляется отображение полученного дискретного сигнала:

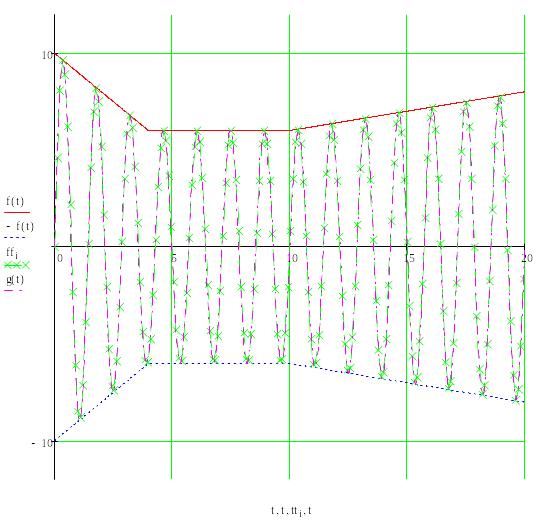
3. Сдвиг и нормировка.

Распределения дискретного сигнала по уровням квантования можно добиться путём нормировки и сдвига исходного сигнала.

Для этого задается число уровней квантования

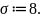
Определяется цена деления аргумента для квантования функции на заданное число уровней

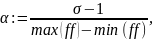
где max(ff) и min(ff) – максимальное и минимальное значения исходного дискретного сигнала соответственно.

Исходный сигнал f(t) в выбранных координатах будет определяться следующим образом:

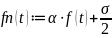
Дискретный сигнал будет иметь следующий вид:

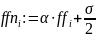
Функци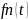и и имеют следующий вид:

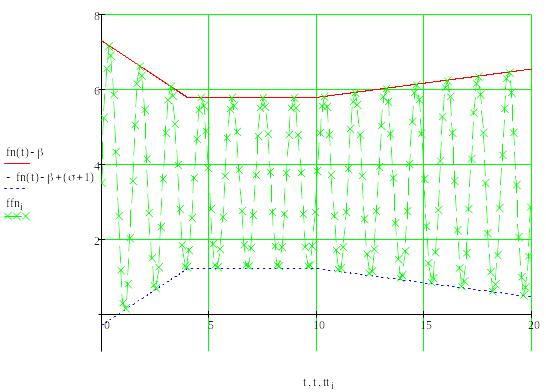
4. Квантование.

Округляем значения дискретного сигнала :

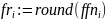
Квантованные отсчёты имеют следующий вид:

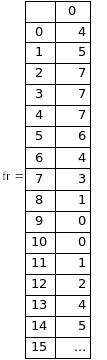
Далее на одном рисунке строятся функции 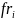и . Число делений (Number of grid) задается как .

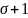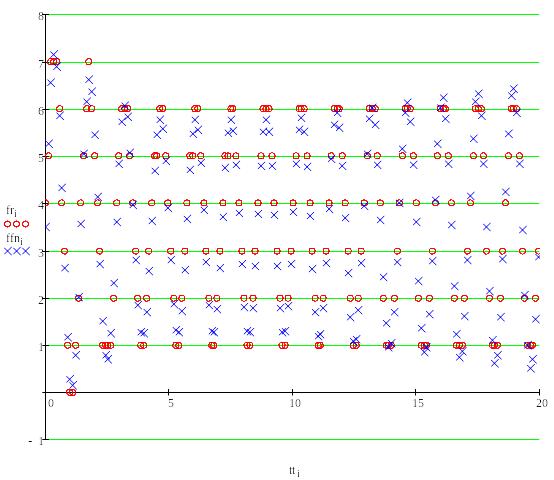
5. Вычисление ошибки квантования.

При округлении дискретной функции до соответствующих уровней квантования возникает ошибка квантования, которую можно рассчитать следующим образом:

.

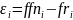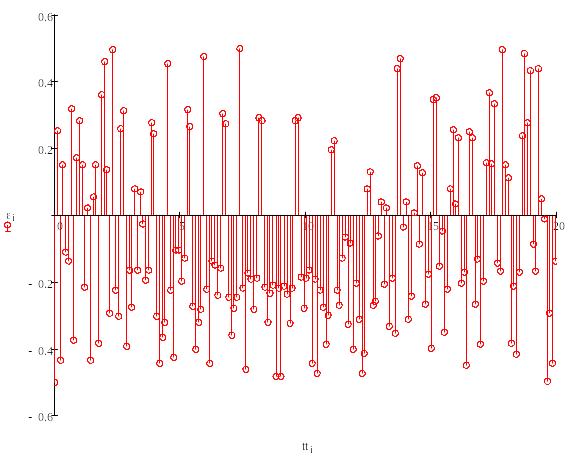
Далее строится график ошибки квантования . Для преобразования графика в нужный вид необходимо в качестве типа графика (type) задать значение stem.

6. Вид цифрового сигнала.

Для получения отсчётов цифрового сигнала необходимо значения квантованного сигнала перевести в двоичный код. В итоге получим следующую последовательность:

100 101 111 111 111 100 100 011 001 000 000 …

7. Восстановление радиосигнала.

Для восстановления сигнала используется функция отсчетов. Сначала задается диапазон изменения аргумента функции и ее шаг:

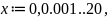
а затем функция отсчетов:

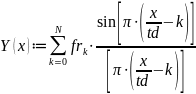
График функции 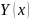имеет вид:

8. Сравнение с исходным сигналом.

Полученный сигнал сравнивается с исходным по следующей формуле:

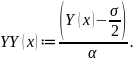
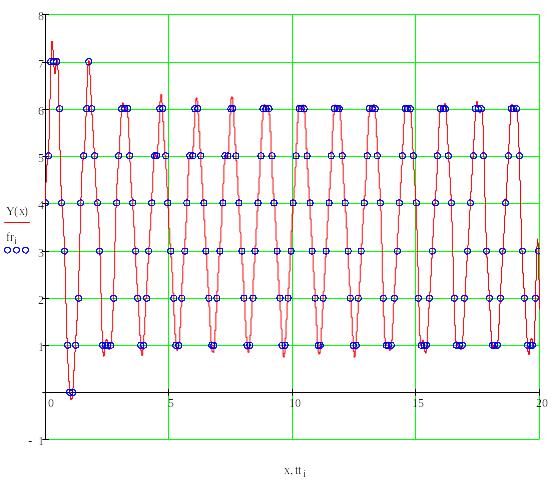
График функции 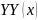имеет следующий вид:

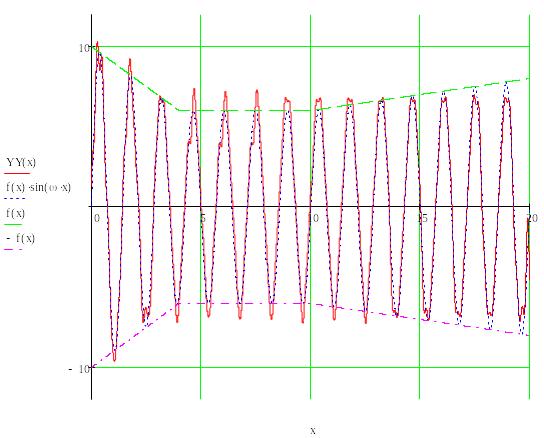
Ошибка восстановления сигнала определяется следующим образом:

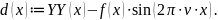
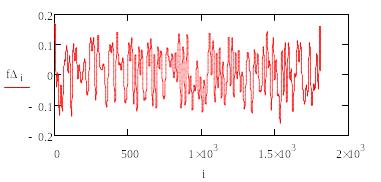
График ошибки имеет следующий вид:

Также определяется среднеквадратичная ошибка:

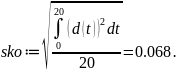
Максимальная ошибка управления рассчитывается следующим образом:

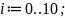
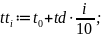
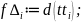
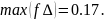
Варианты заданий для лабораторной работы №1

№	Вид огибающей	Частотота несущей 	Частота дискретизации d, кГц	Количество уровней квантования
1		0.75	60; 42	8; 16
2		0.7	57; 27	8; 32
3		0.45	65; 35	16; 32
4		0.73	58; 30	8; 16
5		0.9	61; 29	8; 32
6		0.8	62; 34	16; 32
7		0.7	62; 44	8; 16
8		0.81	63; 34	8; 32
9		0.47	68; 29	16; 32
10		0.91	70; 33	8; 16
11		0.82	72; 30	8; 32
12		0.76	68; 35	16; 32
13		0.42	67; 40	8; 16
14		0.87	75; 32	16; 32
15		0.92	70; 25	8; 32
16		0.55	72; 33	8; 16
17		0.73	67; 37	16; 32
18		0.5	66; 34	8; 16
19		0.5	71; 44	8; 32
20		0.89	62; 26	16; 32
21		0.61	65; 37	8; 16
22		0.69	66; 34	8; 32
23		0.48	69; 37	16; 32
24		0.85	65; 34	8; 16
25		0.62	63; 33	8; 32