Численное решение уравнения Блека-Шоулза
2.1 Основные понятия
Выше было получено уравнение Блека-Шоулза, описывающее изменение стоимости опциона (1.4.6), а также начальное (1.5.1) и граничные условия (1.5.2). Задачу (1.4.6.)-(1.5.1) или (1.5.2) будем называть задачей (I). Теперь перейдем к рассмотрению вопроса численного решения этой задачи. Для того чтобы написать разностную схему, приближенно описывающую данную задачу, нужно совершить следующие два шага [5].
Необходимо заменить область непрерывного изменения аргументов областью его дискретного изменения.
Необходимо заменить дифференциальный оператор некоторым разностным оператором, а также сформулировать разностный аналог для краевых и начальных данных.
После осуществления данной процедуры мы приходим к системе алгебраических уравнений. Таким образом, задача о численном решении исходного дифференциального уравнения сводится к вопросу о нахождении решения полученной алгебраической системы.
Исходная область заменяется множеством точек в этой области, а приближенное решение ищется на этом множестве. Такое множество точек называется сеткой, а отдельные точки называются узлами сетки. Функция, определенная в узлах сетки, называется сеточной функцией.
Таким образом, мы заменили область непрерывного изменения аргумента сеткой, то есть областью дискретного изменения аргумента; иными словами мы осуществили аппроксимацию пространства решений дифференциального уравнения пространством сеточных функций.
Рассмотрим разностную аппроксимацию
дифференциальных операторов. Пусть дан
дифференциальный оператор
,
действующий на функцию
.
Введем на оси x
равномерную сетку с шагом h.
Заменяя входящие в
производные разностными отношениями,
мы получим разностное выражение
,
являющееся линейной комбинацией значений
сеточной функции
на некотором множестве узлов сетки,
называемом шаблоном:
,
где
— коэффициенты,
— шаблон в точке x.
Такая приближенная замена
на
называется аппроксимацией дифференциального
оператора разностным оператором.
Рассмотрим аппроксимацию для оператора
вида:
.
Фиксируем некоторую точку x оси
Ox и возьмем точки x – h и x+h,
где h > 0. Для аппроксимации можно
воспользоваться одним из следующих
выражений:
-
(2.1.1)
(2.1.2)
Выражение (2.1.1) называют правой разностной
производной, а выражение (2.1.2) –
левой разностной производной. Кроме
того, в качестве разностной аппроксимации
можно взять линейную комбинацию выражений
(2.1.1) и (2.1.2):
,
где
— любое вещественное число. При
получается центральная разностная
производная:
-
(2.1.3)
Однако, возникает вопрос – какую ошибку
мы допускам, используя ту или иную
разностную аппроксимацию. Величину
называют погрешностью разностной
аппроксимации
в точке x. Разложим
функцию
по формуле Тейлора:
-
(2.1.4)
При этом мы предполагаем, что функция – достаточно гладкая в некоторой окрестности (x-ho,x+ho), h < ho, а ho – некоторое фиксированное число.
Подставляя (2.1.4) в выражения (2.1.1), (2.1.2) и (2.1.3), мы можем получить:
Будем говорить, что
аппроксимирует дифференциальный
оператор
с порядком m > 0 в
точке x, если:
-
(2.1.5)
Таким образом, левые и правые производные аппроксимируют дифференциальный оператор с первым порядком, а центральная разностная производная – со вторым порядком.
Для того чтобы написать разностную
аппроксимацию второй производной
,
необходимо использовать три точки (x-h,
x, x+h).
В этом случае мы получаем разностный
оператор вида:
-
.(2.1.6)
С учетом выражений для левой и правой
разностных производных, можем переписать
выражение (2.1.6) в виде:
.
Пользуясь разложением функции по формуле Тейлора, нетрудно показать, что порядок аппроксимации в этом случае равен двум [5].
Мы рассмотрели локальную разностную
аппроксимацию, то есть аппроксимацию
в точке. Обычно требуется оценка порядка
разностной аппроксимации для всей сетки
в целом. Пусть
- сетка в некоторой области G
евклидова пространства,
- линейное пространство сеточных функций,
заданных на
,
-
пространство гладких функций u(x),
- норма в
,
- норма в
.
Мы предполагаем, что 1) существует такой
оператор
,
что
для любого
и
2) нормы
и
согласованы, то есть:
,
где |h| -норма вектора
h.
Рассмотрим некоторый оператор L,
заданный в
,
и оператор
,
преобразующий сеточную функцию
в сеточную функцию
,
заданную на
.
Назовем погрешностью аппроксимации
оператора L разностным
оператором
сеточную функцию:
,
где
,
,
u – функция из
.
Если
при
,
то говорят, что разностный оператор
аппроксимирует дифференциальный
оператор L. Будем
говорить, что разностный оператор
аппроксимирует дифференциальный
оператор с порядком m,
если:
.
Перейдем к рассмотрению различных
разностных схем для параболического
уравнения
с краевыми и начальными условиями какими
Рассмотрим семейство шеститочечных
схем. Введем сетки:
,
и сетку
с шагами
.
Обозначим через
значение в узле
сеточной функции y,
определенной на
.
Заменяя
первой разностной производной, а
- второй разностной производной
и вводя произвольный вещественный
параметр ,
рассмотрим однопараметрическое семейство
разностных схем:
|
(2.1.7) ( |
где
.
Схему (2.1.7) будем называть схемой
с весами.
Краевые и начальные условия аппроксимируем точно:
|
(2.1.8) ( |
Разностную задачу, определяемую условиями (2.1.7)-(2.1.8), будем называть задачей (II). Разностная схема (2.1.7) написана на шеститочечном шаблоне, приведенном на рисунке ниже:
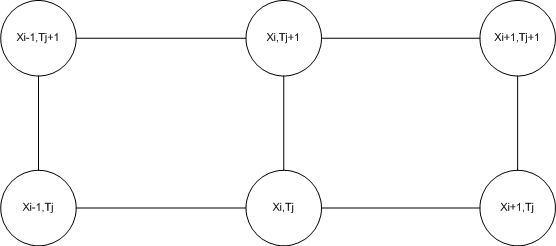
Множество узлов сетки
,
лежащих на прямой
,
обычно называют слоем. Схема (2.1.7)
содержит значения искомой функции y
на двух слоях и поэтому называется
двухслойной схемой.
Рассмотрим схемы, соответствующие
частным значениям
.
При
= 0 получаем четырехточечную схему:
.
Иначе можно записать:
|
(2.1.9) |
Значение
в каждой точке нового слоя
выражается по новой формуле (2.1.9) через
значения
на предыдущем слое
.
Так как при t = 0
задано начальное условие, то формула
(2.1.9) позволяет последовательно определить
значения y на любом
слое. Схема (2.1.9) называется явной.
Если
,
то схема (2.1.7) называется неявной
двухслойной схемой. При
для определения
на новом слое получаем систему
алгебраических уравнений:
|
(2.1.10) |
При
получаем не получаем
схему с опережением или чисто неявную
схему:
|
(2.1.11) |
При
получаем
шеститочечную симметричную схему,
иногда называемую схемой Кранка-Никольсона):
|
(2.1.12) |
Перейдем к рассмотрению вопроса точности
схемы (2.1.7)-(2.1.8). Сравним решение
задачи (II) с решением
u=u(x,t)
задачи (I). Необходимо
рассмотреть разность:
.
Перейдем к безиндексным обозначениям,
полагая:
.Перепишем
задачу (2.1.7)-(2.1.8) в виде:
|
(2.1.13) |
Подставляя y=z+u в (2.1.13) и считая u заданной функцией, получим для z задачу:
,
где
- погрешность аппроксимации задачи (II)
на решении u=u(x,t)
задачи (I). Несложно
получить порядок аппроксимации для
рассмотренных выше схем [5]. Обозначение
означает, что функция u
имеет m производных
по x и n
производных по t. Схема
(2.1.7) при
=0.5
имеет аппроксимацию
,
если
.
При любом
схема (2.1.7) имеет аппроксимацию
,
если
.
Рассмотрим вопрос устойчивости разностной схемы (II). Схема называется устойчивой, если для решения задачи (II) с однородными граничными условиями верна оценка:
|
(2.1.14) |
где M – положительная
постоянная, не зависящая от h
и
,
- некоторая норма на сетке
.
Разностная схема называется условно
устойчивой, если она устойчива при
наличии связи между h
и
,
и безусловно устойчивой в противном
случае. Схема, устойчивая при любых h
и
,
называется абсолютно устойчивой.
Рассмотрим некоторые частные случаи:
Явная схема ( =0) является устойчивой лишь при условии:
|
(2.1.15) |
То есть явная схема условно устойчива.
Неявная схема при
устойчива при любых h
и
.
Таким образом, схема с опережением и
схема Кранка-Никольсона абсолютно
устойчивы.
Сходимость схемы (II) следует из ее устойчивости и аппроксимации. Согласно теореме [5]: Если схема (II) устойчива и аппроксимирует задачу (I), то она сходится, причем порядок ее точности совпадает с порядком ее аппроксимации.