1.6.1. Розрахунок імовірності очікування

Імовірність очікування обслуговування – це імовірність того, що виклик, який надійшов, не буде обслужений негайно, а очікуватиме початку обслу­говування протягом певного часу. Ця імовірність визначається за другою формулою Ерланга, яка визначає імовірність очікування при обслуговуванні виклику пучком із v ліній, на який надходить простий потік викликів з навантаженням Ерл.:

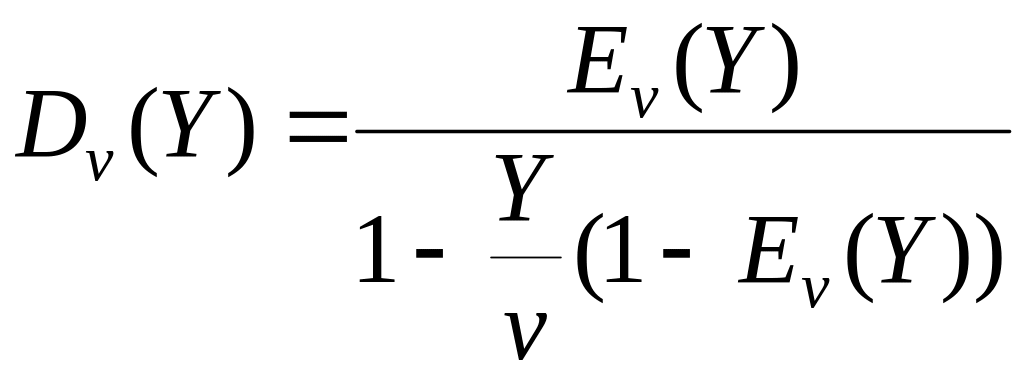, (4)

де – втрати повнодоступного пучка, що визначаються за першою формулою Ерланга.

Для визначення імовірності очікування у формулу підставляємо значення кількості ліній, отримане в п. 1.5.1.

Отже, можна порівняти якість обслуговування КС з блокуванням і КС з очікуванням при однаковій вартості цих комутаційних систем.

1.6.2. Розрахунок умовних втрат

Втрати за часом , чи – імовірність того, що виклик, що надійшов, буде обслужений після деякого часу очікування, не дозволяють достат­ньою мірою охарактеризувати якість обслуговування комутаційною системою з очікуванням потоку викликів, що надходить. Отримана характеристика визначає частину викликів, обслуговування яких відбувається після деякого часу очікування, проте не дає відповіді на питання: як розподіляється час очікування початку обслуговування для викликів, що потрапляють в чергу. Для отримання відповіді на це запитання знайдемо – імовірність того, що виклик, який надійшов в довільний момент часу, потрапить на очікування і час очікування буде більше .

Отже, умовні втрати – це імовірність того, що час очікування буде більшим від допустимого часу очікування .

При розрахунку умовних втрат приймається, що тривалість обслуговування викликів розподілена за експоненційним законом:

(5)

У загальному випадку, вираз для розрахунку умовних втрат має вигляд:

, (6)

де – інтенсивність обслуговування; – допустимий час обслуговування.

Якщо за одиницю вимірювання часу і прийняти середню тривалість одного зайняття , то , а – час, виражений в умовних одиницях часу:

(7)

Тоді, умовні втрати для всіх викликів, що надійшли:

(8)

Умовні втрати для всіх очікуючих викликів:

(9)

Побудувати графічну залежність та від .

Знайти умовні втрати всіх поступивших і очікуючих викликів для допустимого середнього часу очікування та .

1.6.3. Розрахунок середнього часу очікування

До характеристик процесу обслуговування потоку викликів, що надходить у системах з очікуванням, крім і належать:

• середній час очікування початку обслуговування 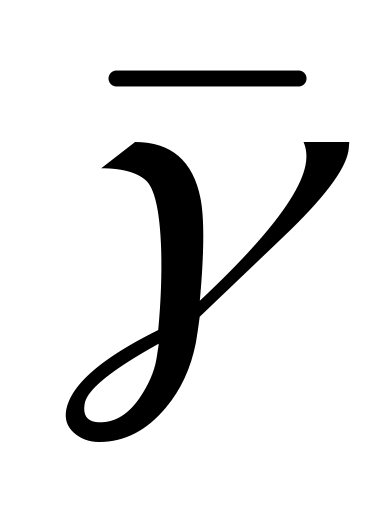, віднесеного до всіх викликів, що надійшли;

• середній час очікування початку обслуговування 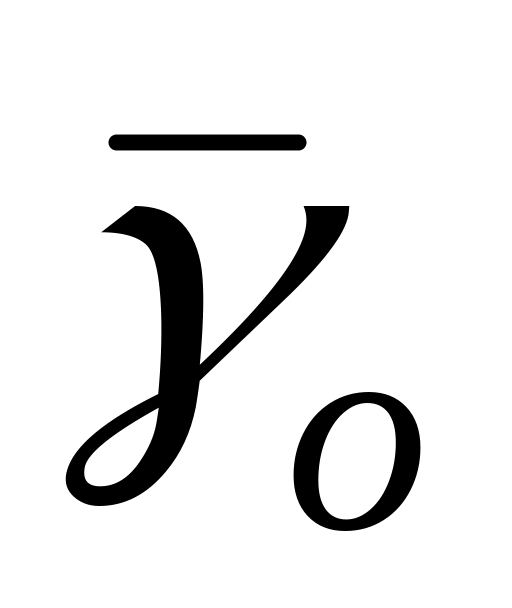, віднесеного до всіх очікуючих викликів;

• середня довжина черги .

Визначимо ці величини.

(10)

Отже, середній час очікування початку обслуговування по відношенню до всіх викликів, що надійшли при , знаходимо за формулою:

. (11)

Середній час очікування початку обслуговування, віднесений тільки до затриманих викликів:

, (12)

а при

. (13)