2. Порядок оформлення звіту

1. Постановка завдання і мета роботи.

1. Стислі теоретичні відомості.

2. Хід виконання роботи.

3. Таблиці, графіки, результати розрахунків.

5. Висновки.

3. Контрольні запитання

1. Що таке потік телефонних викликів?

2. Якими характеристиками можна описати потік телефонних викликів.

3. Що таке одне годино-зайняття?

4. Що таке інтенсивність навантаження і в чому її вимірюють?

5. Як зміниться інтенсивність навантаження, якщо зменшити середню тривалість одного виклику?

6. Від яких величин залежить інтенсивність надходження викликів λ?

7. Які ви знаєте види навантаження?

8. Що таке обслужене навантаження?

9. Що таке година найбільшого навантаження?

Лабораторна робота №3

Вивчення основних характеристик потоків

телефонних викликів

Мета роботи:

Ознайомитися з основними характеристиками потоків телефонних викликів.

1. Порядок виконання роботи

1. Студент перед початком лабораторної роботи ознайомлюється з темою, метою і теоретичними відомостями до лабораторної роботи, пише коротку підготовку, яка включає перелік характеристик телефонного навантаження, а також потоків телефонних викликів.

2. Кожен студент отримує індивідуальне завдання, яке містить:

– сумарний час моделювання, виражений в годинах;

– середня тривалість виклику (середній час обслуговування виклику), с;

– середня кількість викликів від одного абонента за одиницю часу;

– кількість джерел викликів.

3. Виконати програму ОК_lab1.exe, в основному діалоговому вікні якої вибрати пункт 3 – «простий і примітивний потоки викликів».

У діалоговому вікні ввести вихідні дані згідно з своїм варіантом і натиснути кнопку «Starting …».

4. Після закінчення моделювання потоку викликів на екрані ми отримали такі результати:

а) Розподіл Пуассона – теоретичний розподіл, побудований за формулою:

,

де – інтенсивність надходження викликів (параметр потоку) від абонентів протягом години; – інтервал спостереження, заданий вихідними даними варіанта; – імовірність надходження i викликів на проміжку часу .

b) Розподіл Бернуллі – теоретичний розподіл, що відповідає примітивному потоку викликів, описується формулою

, де – кількість комбінацій, – інтенсивність навантаження від одного абонента, – кількість абонентів.

c) Згенерований розподіл – отриманий практичний розподіл імовірності надходження викликів у результаті моделювання.

Результати а), b) та с) отримані для однакових параметрів , , і показані на рис. 1: розподіл Пуассона – жовта крива, розподіл Бернуллі – рожева, згенерований розподіл – зелена крива.

d) Розподіл тривалості викликів, показаний також на рис. 2 – червона крива.

Результати 1, 2, 3 – це послідовності кількості викликів на інтервалі , а також моменти надходження викликів і тривалості викликів відповідно.

5. Зобразити рис. 1 у звіті до лабораторної роботи, порівняти теоретичні і отриманий шляхом імітаційного моделювання розподіли. Зобразити рис. 2 і зробити висновок про залежність імовірності виникнення від величини тривалості виклику.

6. Знайти:

• інтенсивність надходження викликів λ, яку шукаємо за формулою:

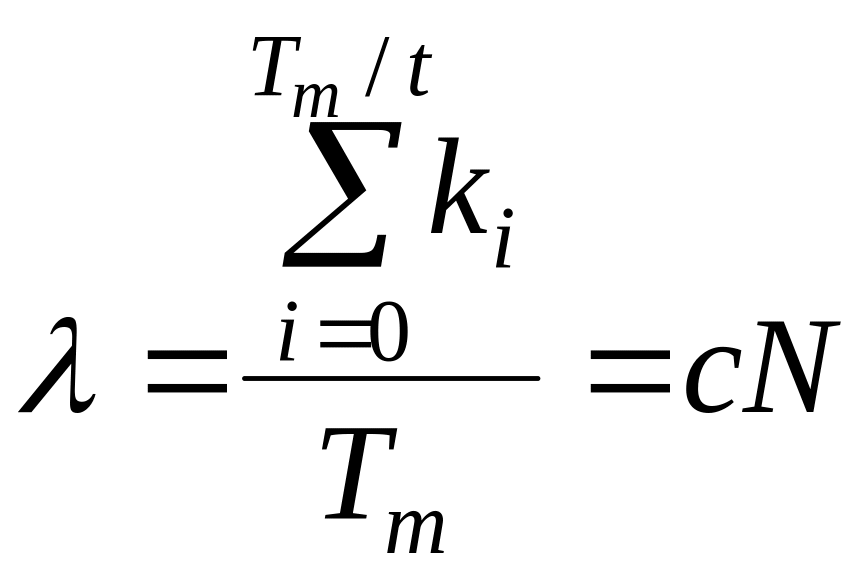, викликів/годину;

де в чисельнику – сумарна кількість викликів, що надійшли на вхід системи масового обслуговування протягом часу моделювання (сума послідовності 1).

• середню тривалість виклику:

,

де – сумарна кількість викликів, що надійшли в систему, – тривалість кожного виклику.

7. Знайти середню інтенсивність навантаження, що створюється N абонентами:

.

8. Знайти середню інтенсивність навантаження від одного абонента, як:

.

9. Знайти математичне очікування і дисперсію кількості викликів на інтервалі часу для теоретичного а), b) і практичного с) розподілів і за отриманими результатами зробити висновки.

Математичне очікування випадкової величини знаходимо за формулою:

;

Дисперсію обчислюємо за формулою

10. Зробити висновки до лабораторної роботи.