2. Средние величины
Средняя величина - обобщающая характеристика однотипных явлений по одному из варьирующих признаков.
Определить среднюю можно через исходное соотношение средней (ИСС) или ее логическую формулу:
Для изучения и анализа социально-экономических явлений процессов применяются различные средние величины: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая, а также структурные средние: мода, медиана, квартили, децили. Средние могут рассчитываться в двух вариантах: взвешенные и невзвешенные (табл. 1).
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях единицы). Тогда используют формулу средней:
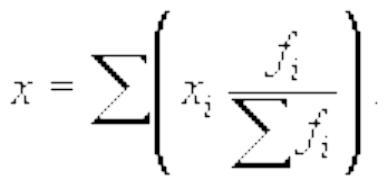
В интервальном вариационном ряду для расчета средней арифметической взвешенной определяются и используются значения середины интервалов.
Таблица 1
Виды степенных средних
Рассмотрим методологию применения разных видов степенных средних на основе расчета средней заработной платы по двум предприятиям вместе: за январь, февраль и за два месяца. Исходные данные представлены в табл. 2.
Таблица 2
Определим исходные соотношения средней для показателя «средняя заработная плата»:
За январь мы располагаем данными о средней заработной плате и численности работников, т. е. нам известен знаменатель исходного соотношения, но неизвестен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
где xi - i-й вариант осредняемого признака;
fi - вес i-го варианта.
За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда, т. е. нам известен числитель исходного соотношения, но неизвестен знаменатель. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда средняя заработная плата в целом по двум предприятиям будет рассчитываться по формуле средней гармонической взвешенной:
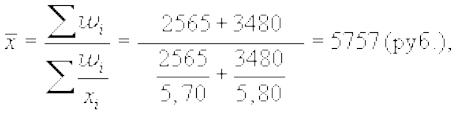
За два месяца средняя заработная плата по двум предприятиям определяется по формуле средней арифметической простой (невзвешенной), так как веса (f) отсутствуют или равны.
где n - число единиц, или объем совокупности.
Таким образом, исходя из приведенных данных, были применены разные виды степенных средних.
Средняя геометрическая используется в анализе динамики для определения среднего темпа роста.
Средняя квадратическая и степенные средние более высоких порядков используются при расчете ряда статистических показателей, характеризующих вариацию и взаимосвязь.
Мода - величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Для интервальных рядов распределения с равными интервалами мода (Мо) определяется по формуле:
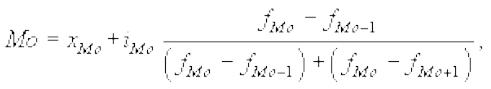
где xMo - начальное значение интервала, содержащего моду;
iMo - величина модального интервала;
fMo - частота модального интервала;
fMo - 1 - частота интервала, предшествующего модальному;
fMo +1 - частота интервала, следующего за модальным
Медиана - варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
В интервальном вариационном ряду медиана рассчитывается по формуле:
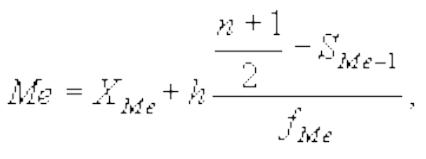
где XMe - нижняя граница медианного интервала;
h - ширина интервала;
SMe-1 - накопленная частота интервала, предшествующего медианному;
fMe - частота медианного интервала.