5. Расчет индекса сезонности

Для получения  проведем осреднение уровней одноименных периодов по формуле простой средней арифметической:

январь —

февраль —

…

декабрь —

Далее по исчисленным месячным средним уровням  определяем общий средний уровень по формуле средней арифметической взвешенной, где n — число месяцев.

В завершение определяют индексы сезонности по месяцам года по формуле:

Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна, изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца.

Однако помесячные данные одного года из-за элемента случайности могут быть ненадежными для выявления закономерности колебаний. Поэтому на практике используются помесячные данные за ряд лет (обычно не менее трех лет). Тогда для каждого месяца рассчитывается средняя величина уровня за три года, затем определяются среднемесячный уровень для всего ряда и отношение средних для каждого месяца к общему среднемесячному уровню ряда (в процентах).

Тема 1.9. Экономические индексы

Вопросы темы:

1. Понятие индексов. Их виды

2. Расчет сводного индекса

3. Расчет среднеарифметического индекса

4. Расчет среднегармонического индекса

5. 5. Расчет индексов средних величин

1. Понятие индексов. Их виды

Индексы - важнейший обобщающий показатель. С их помощью можно измерить динамику социально-экономического явления за два или более периодов времени, динамику среднего показателя и сопоставить уровни явления в пространстве, по странам, экономическим районам, областям и т. д. Индексы используются для определения степени влияния изменений значений одних показателей на динамику других, а также для пересчета значений макроэкономических показателей из фактических цен в сопоставимые.

Простейший показатель, применяемый в индексном анализе, индивидуальный индекс, который характеризует изменение во времени или в пространстве отдельных однородных элементов совокупности. Например, индивидуальные индексы физического объема продукции, цен, себестоимости единицы продукции.

В экономических расчетах чаще всего используются сводные, или общие, индексы, которые характеризуют изменение совокупности в целом.

Построение этих индексов является содержанием индексной методологии, в которой сложились две концепции: синтетическая и аналитическая.

Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных явлений, отдельные части которых непосредственно несоизмеримы, и поэтому индексы - показатели синтетические.

В соответствии с аналитической концепцией индексы трактуются как показатели, необходимые для измерения влияния изменения составных частей, факторов сложного явления на изменение уровня этого явления. Поэтому индексной методологией предусматривается определение влияния каждого из факторов путем элиминирования влияния других факторов на уровень изучаемого явления. Такие индексы - показатели аналитические.

Общие индексы строят для количественных и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатную или средневзвешенную.

При построении агрегатного индекса необходимо решить проблему выбора весов, при этом руководствуются следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период; если строится индекс качественного показателя, то используются веса отчетного периода.

В статистической практике, помимо агрегатных, применяются средневзвешенные индексы: среднеарифметический и среднегармонический.

Индексный метод служит также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.

Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующими изменение индексируемого (осредняемого) показателя.

Индекс переменного состава (I_пер.с) для качественных показателей имеет следующий вид:

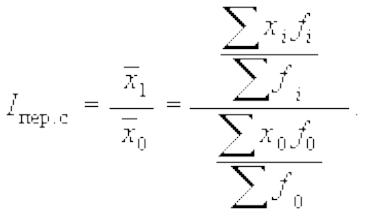
Величина этого индекса характеризует изменения средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.

Индекс постоянного состава (I_п.с) учитывает изменения только индексируемой величины, показывает средний размер изменения изучаемого показателя у единиц совокупности и выглядит следующим образом:

Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:

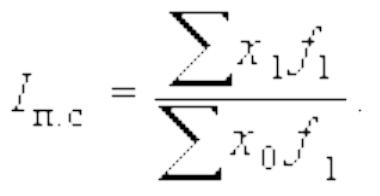
Индекс структурных сдвигов (I_{стр.сдв}) характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:

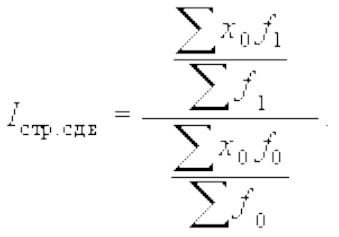
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d).

В индексах средних уровней могут быть взяты в качестве весов удельные веса единиц совокупности. Тогда систему индексов можно представить так:

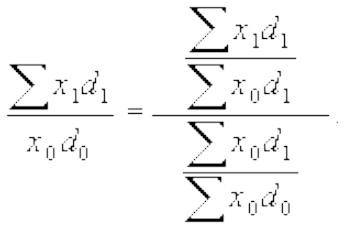
Система взаимосвязанных индексов имеет следующий вид:

I_пер.с = I_п.с х I_{стр.сдв.}

При изучении динамики социально-экономических явлений за некоторый интервал времени, включающий в себя более двух периодов времени, используется система индексов: цепные индексы с переменными весами; цепные индексы с постоянными весами, базисные индексы с переменными весами, базисные индексы с постоянными весами.

Для сравнения (сопоставления) показателей в пространстве (по странам, экономическим районам, областям и т. п.) применяются территориальные индексы.

В рыночной экономике особую роль играют индексы цен, которые позволяют оценить динамику цен на товары, измерить инфляцию при макроэкономических исследованиях, пересчитать важнейшие стоимостные показатели системы национальных счетов (СНС) из фактических цен в сопоставимые и др. Для решения различных задач могут быть использованы индексы цен Г. Пааше и Э. Ласпейреса. Весами в индексе Г. Пааше выступает количество продукции текущего периода, а в индексе цен Э. Ласпейреса - количество продукции базисного периода.

Средняя геометрическая из произведения двух агрегатных индексов цен Э. Ласпейреса и Г. Пааше представляет собой индекс цен И. Фишера.

Пересчет в основных стоимостных показателях СНС из фактических цен в сопоставимые осуществляется с помощью индекса-дефлятора. В основе расчета индекса-дефлятора лежит формула Г. Пааше - агрегатная формула с текущими весами.