4. Определение объема выборки
Необходимый объем выборки (n) с заранее заданным значением допустимой ошибки, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения, устанавливают, исходя из формул ошибок выборки (табл. 3).
Пример 5. Численность сотрудников таможенного органа — 342 человека. В порядке случайной бесповторной выборки предполагается определить средний размер денежного довольствия сотрудника таможенного органа при условии, что средняя ошибка не должна превышать 100 руб. с вероятностью 0,954 и при среднем квадратическом отклонении 1563 руб. (ошибка и среднее квадратическое отклонение найдены на основе пробного обследования).
Так как при p =0,954, t = 2, необходимая численность выборки равна:
Следовательно, для обследования при заданных условиях необходимо отобрать 253 человека
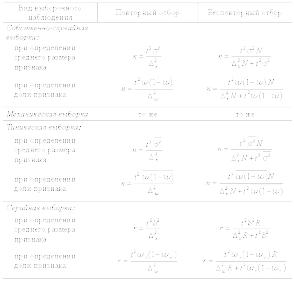
Таблица 3.
Формулы ошибок выборки
Тема 1.7. Статистическое изучение взаимосвязи социально-экономических явлений
Вопросы темы:
1. Виды статистической связи
2. Методы изучения статистической связи
1. Виды статистической связи
Изучение взаимосвязей на рынке товаров и услуг - важнейшая функция работников коммерческих служб: менеджеров, коммерсантов, экономистов. Особую актуальность оно приобретает в условиях развивающейся рыночной экономики. Изучение механизма рыночных связей, взаимодействия спроса и предложения, влияния объема и состава предложения товаров на объем и структуру товарооборота, формирования товарных запасов, издержек обращения, прибыли и других качественных показателей имеет первостепенное значение для прогнозирования конъюнктуры рынка, рациональной организации торговых процессов и решения многих вопросов успешного ведения бизнеса.
Статистика призвана изучать коммерческую деятельность с количественной стороны. Это осуществляется с помощью соответствующих приемов и методов статистики и математики.
Статистические показатели коммерческой деятельности могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.
Балансовая связь характеризует зависимость между источниками формирования ресурсов (средств) и их использованием:
Он + П =В + Ок,
где Он - остаток товаров на начало отчетного периода;
П - поступление товаров за период;
В - выбытие товаров в изучаемом периоде;
Ок - остаток товаров на конец отчетного периода.
Левая часть формулы (Он + П) характеризует предложение товаров, а правая часть (В + Ок) - использование товарных ресурсов.
Компонентные связи показателей коммерческой деятельности характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель как множители: a = bc.
Факторные связи характеризуются тем, что они проявляются в согласованной вариации изучаемых показателей. При этом одни показатели выступают как факторные, а другие - как результативные.
Факторные связи могут рассматриваться как функциональные и корреляционные.
При функциональной связи изменение результативного признака y всецело зависит от изменения факторного признака x:
y = f (x) .
При корреляционной связи изменение результативного признака y не всецело, а лишь частично зависит от факторного признака x, так как возможно влияние прочих факторов :
y= a + f (x) .
Примером корреляционной связи показателей коммерческой деятельности может служить зависимость сумм издержек обращения от объема товарооборота. В этой связи помимо факторного признака (объема товарооборота x) на результативный признак (сумму издержек обращения y) влияют и другие факторы, в том числе не учтенные. Поэтому корреляционные связи не являются полными (тесными) зависимостями.
Характерная особенность корреляционных связей заключается в том, что они проявляются не в единичных случаях, а в массе.
Регрессия - это функция f (х1; х2; …; хт), которая отражает зависимость средней величины результативного признака от заданных фиксированных значений факторных признаков.
Для выбора вида уравнения можно ориентироваться на график эмпирической линии связи. Наибольшее распространение получили следующие типы функций:
■ линейная yx = a0 + a1x ;
■ парабола второго порядка yx = a0 + a1x + a2x2 ;
■ гипербола
■ показательная
Для установления достоверности уравнения регрессии рассчитываются ошибка аппроксимации и коэффициент детерминации. Если величина ошибки не превышает 10 - 15%, то данное уравнение может быть использовано для практических целей.
При статистическом изучении корреляционной связи показателей коммерческой деятельности перед статистикой ставятся следующие основные задачи:
■ проверка положений экономической теории о возможности связи между изучаемыми показателями и придание выявленной связи аналитической формы зависимости;
■ определение количественных оценок тесноты связи, характеризующих силу влияния факторных признаков на результативные.
Для того чтобы установить, есть ли зависимость между величинами, используются разнообразные статистические методы, позволяющие определить, во-первых, вид связи; во-вторых, тесноту связи (в одном случае она сильная, устойчивая, в другом -слабая); в-третьих, форму связи (т. е. формулу, связывающую величины x и y).
В процессе изучения связи нужно учитывать, что мы используем математический аппарат, но всегда следует иметь теоретические обоснования той связи, которую пытаются показать.