
- •1. Методические рекомендации по организации изучения 4
- •2. Конспект лекций 6
- •1. Методические рекомендации по организации изучения дисциплины
- •2. Конспект лекций Раздел 1. Общая теория статистики Тема 1.1. Предмет, метод и организация статистики
- •1.Предмет общей теории статистики
- •2. Стадии и методы статистического исследования
- •3. Задачи общей теории статистики
- •Тема 1.2. Статистическое наблюдение социально-экономических явлений и процессов
- •1. Сущность статистического наблюдения
- •3. Основные организационные формы, виды и способы статистического наблюдения
- •Тема 1.3. Сводка и группировка статистических данных
- •2. Методика построения группировок.
- •Тема 1.4. Статистические показатели
- •1. Абсолютные и относительные величины
- •2. Средние величины
- •Тема 1.5. Показатели вариации и анализ вариационных рядов
- •1. Понятие вариации. Расчет среднего линейного отклонения
- •2. Расчет дисперсии и среднего квадратического отклонения по
- •3. Расчет дисперсии по формуле по индивидуальным данным
- •4. Показатели относительного рассеивания
- •5. Показатели характеристики вариационных рядов
- •6. Понятие рядов распределения
- •7. Понятие статистических графиков
- •Тема 1.6. Выборочное наблюдение
- •1. Понятие выборочного метода
- •2. Ошибки, возникающие при выборочном наблюдении
- •3. Классификация выборок
- •4. Определение объема выборки
- •Тема 1.7. Статистическое изучение взаимосвязи социально-экономических явлений
- •1. Виды статистической связи
- •2. Методы изучения статистической связи
- •Тема 1.8. Ряды динамики
- •1. Понятие и классификация рядов динамики
- •2. Статистические показатели ряда динамики
- •3. Метод скользящей средней
- •4. Метод аналитического выравнивания
- •5. Расчет индекса сезонности
- •Тема 1.9. Экономические индексы
- •1. Понятие индексов. Их виды
- •2. Расчет сводного индекса
- •3. Расчет среднеарифметического индекса
- •4. Расчет среднегармонического индекса
- •5. Расчет индексов средних величин
- •Тема 1.10. Статистические методы моделирования и прогнозирования социально-экономических явлений и процессов
- •1. Теоретикие основы методов социально-экономического
- •Раздел II. Социально-экономическая статистика Тема 2.1. Предмет, метод и организация статистики
- •1. Предмет социально-экономической статистики
- •2. Статистическая методология. Закон больших чисел.
- •3. Задачи социально-экономической статистики
- •4. Организация получения статистической информации
- •5. Унифицированные формы статистического наблюдения
- •6. Система стандартных классификаций и регистров
- •7. Принципы ведения Генеральной совокупности объектов статистического наблюдения
- •Тема 2.2. Статистика населения
- •1. Статистика населения
- •Тема 2.3. Статистика ранка труда
- •1. Статистика рынка труда, занятости, безработицы, затрат на рабочую силу и оплаты труда
- •Тема 2.4. Баланс активов и пассивов и статистика национального богатства
- •Тема 2.5. Анализ эффективности функционирования предприятий и организаций
- •1.Общие понятия эффективности деятельности.
- •2. Статистика промышленности.
- •3. Статистика инвестиций
- •Тема 2.6. Статистика товарооборота, товарных запасов, потребления и покупательского спроса
- •1. Статистика товарооборота, товарных запасов, потребления и покупательского спроса
- •Тема 2.7. Статистика цен и инфляции
- •1.Система показателей статистики цен и методы расчета
- •3. Статистика цен производителей продукции промышленности
- •4. Статистика цен строительной продукции
- •5. Статистика цен в сельском хозяйстве
- •6. Основные статистические показатели оценки инфляции
- •Тема 2.8. Статистика доходов и потребления населением товаров и услуг
- •1.Показатели доходов населения
- •2. Методы изучения дифференциации доходов населения, уровня
- •Распределение населения по размеру среднедушевого денежного дохода в 2010 г.
- •3. Показатели расходов и потребления населения товаров и услуг
- •Баланс денежных доходов и расходов населения
- •4. Обобщающие показатели уовня жизни населения
- •5. Статистика социальной сферы
- •Раздел 3. Система национальных счетов Тема 3.1. Система нациолнальных счетов.
- •1.Определение и задачи системы национальных счетов
- •2. Теоретико-методологические основы снс
- •3. Снс как система макроэкономических показателей
- •4. Валовой внутренний продукт
- •Тема 3.2. Межотраслевой и платежный балансы
- •1. Межотраслевой баланс
- •Общая схема межотраслевого баланса (базовая таблица в системе таблиц «затраты выпуск»)
- •2.Платежный баланс
- •Раздел IV. Статистика финансов Тема 4.1. Статситика финансов
- •2. Метод статистики финансов
- •3. Задачи статистики финансов
- •4. Статистика государственных финансов
- •5. Основы высших финансовых вычислений
- •6. Статистика финансов предприятий и организаций
- •Тема 4.2. Статситика бюджета и бюджетной системы. Статистика налогообложения
- •1. Статистика бюджета и бюджетной системы
- •2. Статистика налогообложения
- •Тема 4.3. Статситика денежного обращения. Статистика биржевой и банковской деятельности
- •1. Статистика денежного обращения
- •2. Статистика кредита
- •3. Статистика валютного регулирования и валютного контроля
- •4. Статистика рынка ценных бумаг и фондовых бирж
- •5. Статистика банковской деятельности
- •6. Статистика страхования и страхового рынка
- •2 Практикум по дисциплине
- •2.1. Задачи к разделу 1 «Общая теория статистики»
- •2.2. Задачи к разделу 2 «Социально-экономическая статистика»
- •2.3. Задачи к разделу 3 «Система национальных счетов»
- •2.4. Задачи к разделу 4 «Статистика финансов»
- •4 Методические рекомендации преподавателям по эффективным средствам, методам и технологиям обучения дисциплине
- •5 Методические указания по организации самостоятельной работы студентов
- •Конспект лекций.
- •6 Содержание и методика проведения промежуточных аттестаций (экзаменов)
- •Тестовые задания по разделу «Общая теория статистики»
- •Тестовые задания по 2 разделу «Социально-экономическая статистика»
- •Тестовые задания по 3 разделу «Система национальных счетов»
- •Тестовые задания по 4 разделу «Статистика финансов»
2. Расчет дисперсии и среднего квадратического отклонения по
индивидуальным данным и в рядах распределения
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
![]() -
дисперсия невзвешенная (простая);
-
дисперсия невзвешенная (простая);
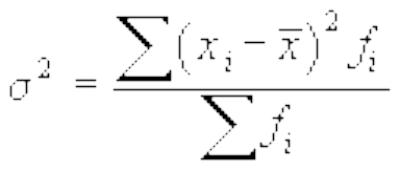 -
дисперсия взвешенная.
-
дисперсия взвешенная.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т. д.).
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
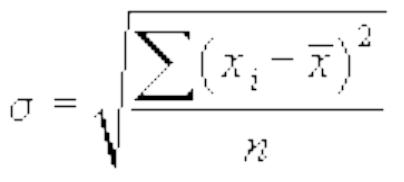 -
среднее квадратическое отклонение
невзвешенное;
-
среднее квадратическое отклонение
невзвешенное;
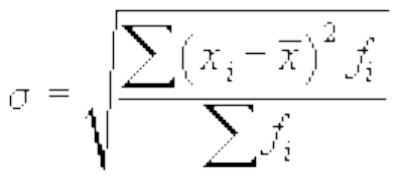 -
среднее квадратическое отклонение
взвешенное.
-
среднее квадратическое отклонение
взвешенное.
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенной следующий:
1) определяют среднюю арифметическую взвешенную:
2) рассчитывают отклонения вариантов от средней:
3) возводят в квадрат отклонение каждого варианта от средней:
![]()
4) умножают квадраты отклонений на веса (частоты):
![]()
5) суммируют полученные произведения:
![]()
6) полученную сумму делят на сумму весов:
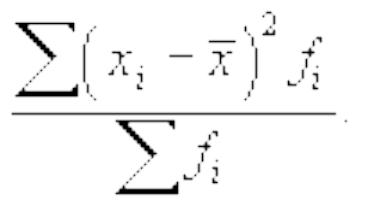
Пример 3. Имеются следующие данные о производительности труда рабочих:
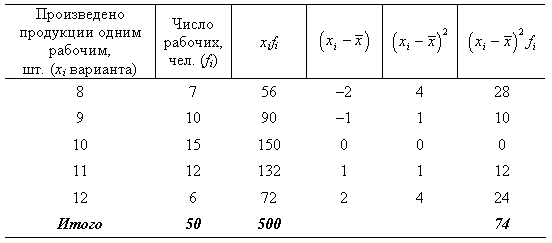
Исчислим среднюю арифметическую взвешенную:
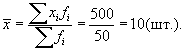
Значения отклонений от средней и их квадратов представлены в таблице. Определим дисперсию:

Среднее квадратическое отклонение будет равно:
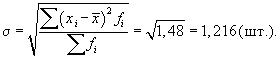
Если исходные данные представлены в виде интервального ряда распределения, то сначала нужно определить дискретное значение признака, а затем применить изложенный метод.
Пример 4. Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы.

Средняя
арифметическая равна:
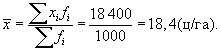
Исчислим
дисперсию:
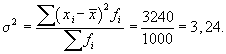
3. Расчет дисперсии по формуле по индивидуальным данным
Техника вычисления дисперсии сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Дисперсия имеет следующие свойства:
1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсию не изменяет.
2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсию не изменяет.
Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в k2 раз, а среднее квадратическое отклонение - в k раз.
Дисперсия признака относительно произвольной величины всегдабольше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:
![]()
Если А больше 0, то приходим к следующему равенству:
![]()
т. е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую;
2) возводят в квадрат среднюю арифметическую;
3) возводят в квадрат отклонение каждого варианта ряда;
4) находят сумму квадратов вариантов;
5) делят сумму квадратов вариантов на их число, т. е. определяют средний квадрат;
6) определяют разность между средним квадратом признака и квадратом средней.
Пример 5. Имеются следующие данные о производительности труда рабочих:
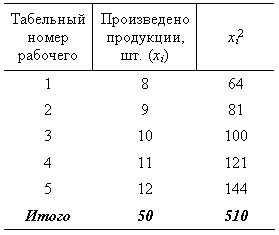
Произведем следующие расчеты:
![]()
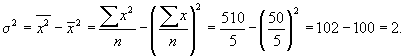
Рассмотрим расчет дисперсии в интервальном ряду распределения.
Порядок
расчета дисперсии взвешенной (по формуле
![]() )
следующий:
)
следующий:
1) определяют среднюю арифметическую;
2) возводят в квадрат полученную среднюю;
3) возводят в квадрат каждый вариант ряда;
4) умножают квадраты вариантов на частоты;
5) суммируют полученные произведения;
6) делят полученную сумму на сумму весов и получают средний квадрат признака;
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т. е. дисперсию.
Пример 6.
Имеются следующие данные о распределении посевной площади колхоза по урожайности пшеницы:
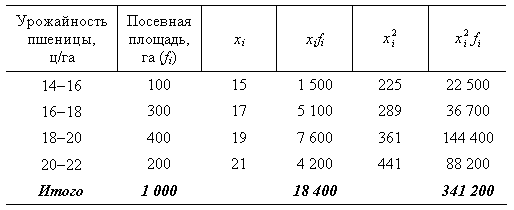
В подобных случаях прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется рассмотренный метод расчета:
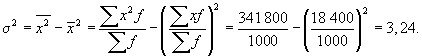
Средняя величина отражает тенденцию развития, т. е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.
