1.4.3 Интегральный показатель качества i2 (квадрат ошибки)

Следующий способ заключается в выборе коэффициентов характеристического полинома из условия минимума среднеквадратической ошибки:

,

здесь – квадрат сигнала ошибки (разность входного и выходного сигналов). Данный критерий позволяет в комплексе минимизировать такие показатели, как длительность переходного процесса, амплитуду и частоту колебаний ошибки, не гарантируя каких-то заданных значений для этих характеристик по отдельности. Ниже приводятся выражения для характеристических полиномов с первого по пятый порядок, полученные из критерия I₂ (расположение корней характеристического уравнения показано на рис. 4):

,

,

,

,

.

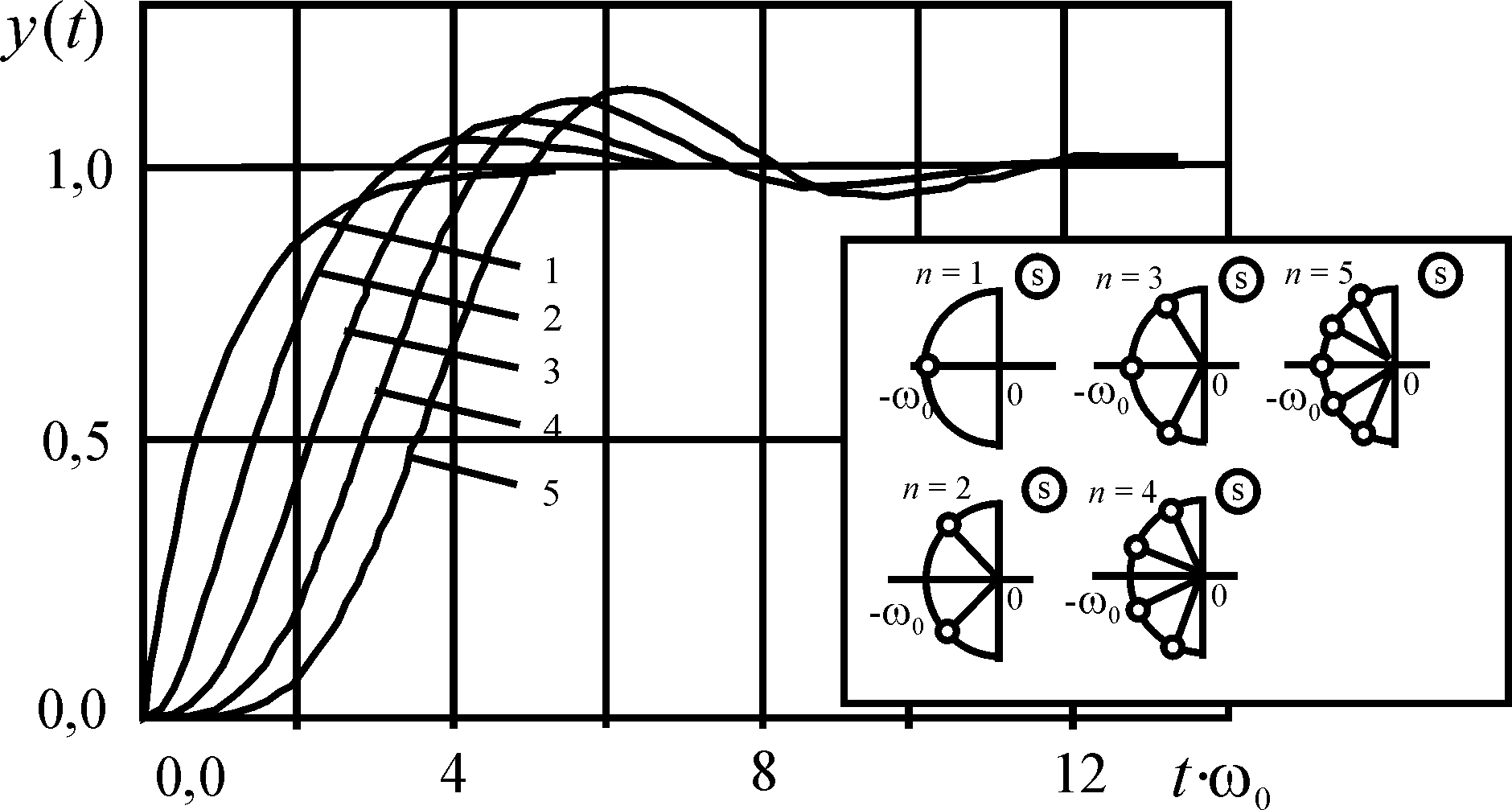
Рис. 3. Расположение корней характеристического уравнения и поведение переходных процессов для схемы Баттерворта

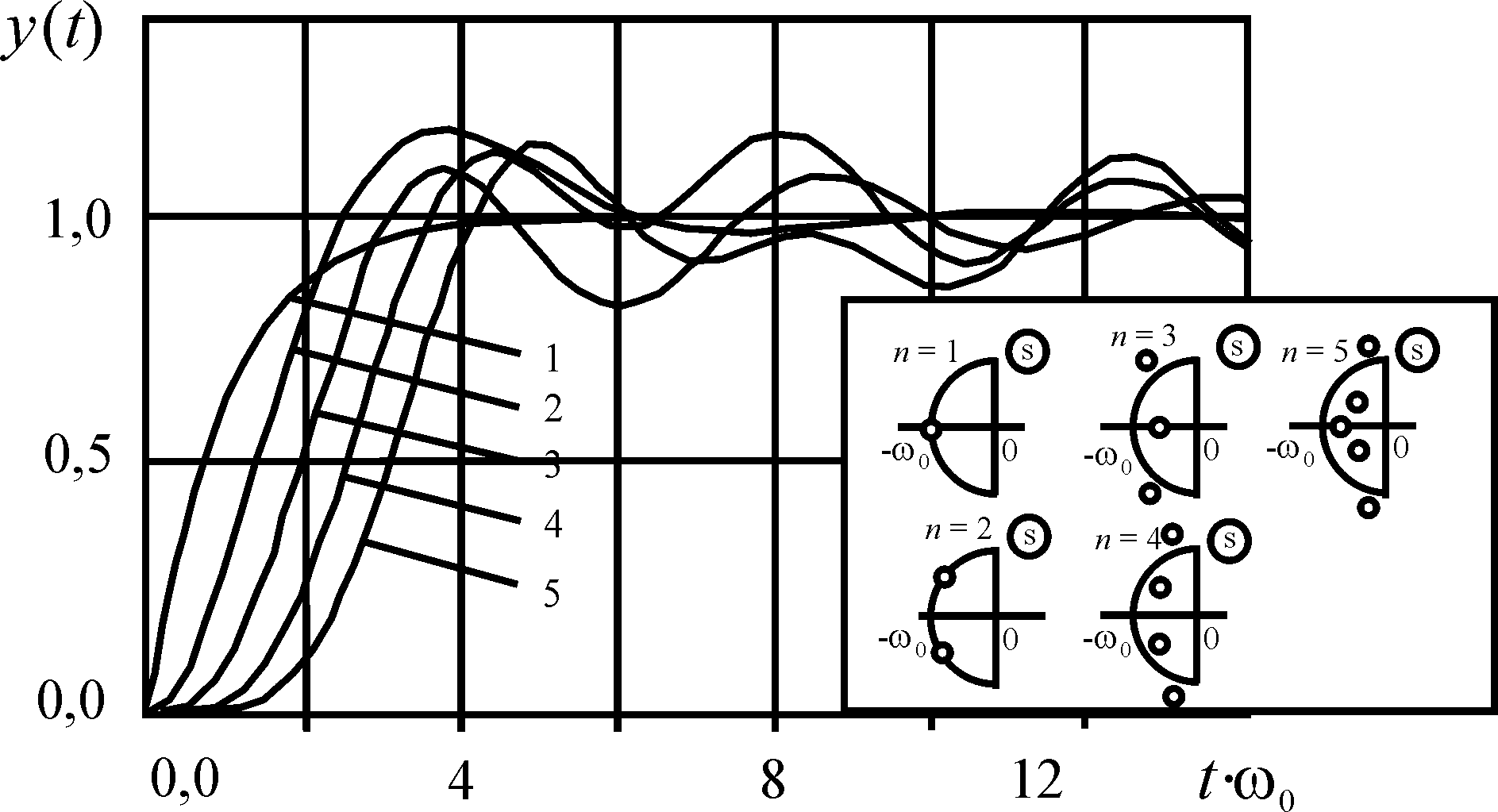
Рис. 4. Расположение корней характеристического уравнения и поведение переходных процессов, минимизирующих критерий I₂

Реакция на ступенчатое воздействие системы, оптимизированной по квадратичному критерию (рис. 4), по сравнению с реакцией системы Баттерворта обладает несколько большей колебательностью.

1.4.4 Интегральный показатель качества i3 (абсолютное значение ошибки)

Кроме указанных, известны стандартные формы характеристических полиномов, получающиеся в результате минимизации оптимизирующего функционала

,

представляющего собой интеграл от произведения абсолютного значения ошибки на время . Реакции на ступенчатое воздействие систем, оптимизированных по данному критерию (рис. 5), по сравнению с реакциями биномиальной системы характеризуются значительно большим быстродействием, а по сравнению с реакциями систем Баттерворта - меньшей колебательностью. Стандартные формы, полученные по данному критерию, находят достаточно широкое применение на практике. Однако какого-либо алгоритма составления этих форм не существует (они получены эмпирически с помощью аналоговых моделирующих установок [5]).

Примеры стандартных полиномов:

,

,

,

,

.

Соответствующие расположения корней характеристического уравнения показаны на рис. 5.

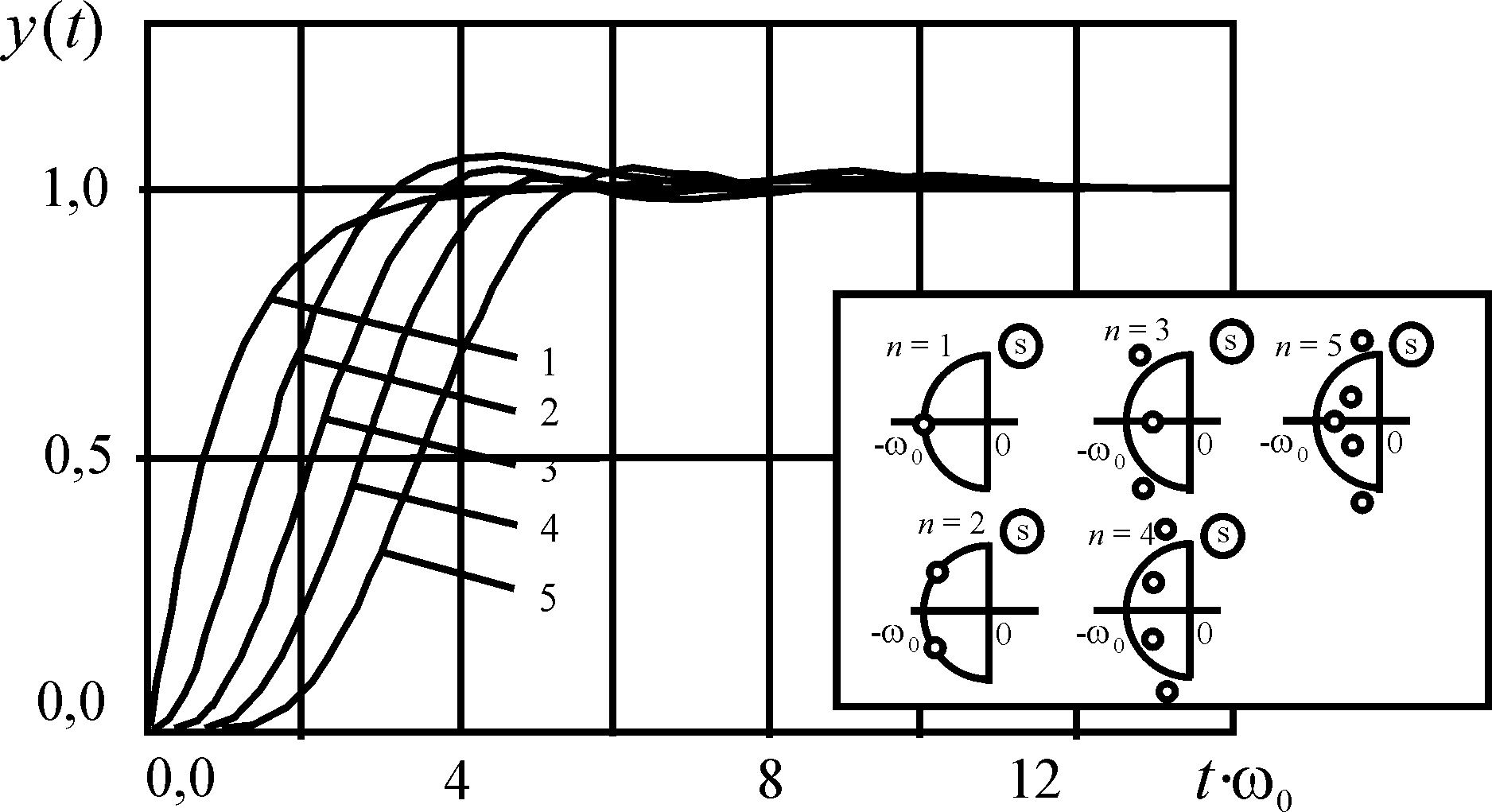
Рис. 5. Расположение корней характеристического уравнения и поведение переходных процессов, минимизирующих критерий I₃

Проиллюстрируем методику синтеза модального регулятора на примере.

2 Пример выполнения работы

Для объекта управления, заданного в виде

,

где W(p) – операторная передаточная функция

,

требуется рассчитать модальный регулятор, обеспечивающий устойчивость, быстродействие и коэффициент усиления замкнутой системы. При расчетах необходимо провести сравнительный анализ результатов, полученных при различных способах назначения корней характеристического полинома эталона.

Решение. Объект управления приведем к стандартному операторному виду; переход осуществляется по формуле

,

откуда операторы и

,

.

Порядок модального регулятора определится по формуле (7):

,

при этом модальный регулятор (2) принимает вид

. (13)

Матрицы уравнения (8) найдутся по формулам (9) - (11):

, , .

Характеристический полином эталона выбирается:

1. по биномиальной схеме

;

2. по схеме Баттерворта

;

3. по интегральному показателю I₂

;

4. по интегральному показателю I₃

.

Составляя и решая уравнение (8), для каждой схемы в отдельности получаем следующие коэффициенты модального регулятора (13):

1) , , ;

2) , , ;

3) , , ;

4) , , .

Графики переходных процессов замкнутой системы представлены на рис. 6 (обозначенные цифрами 1, 2, 3 и 4 соответственно).

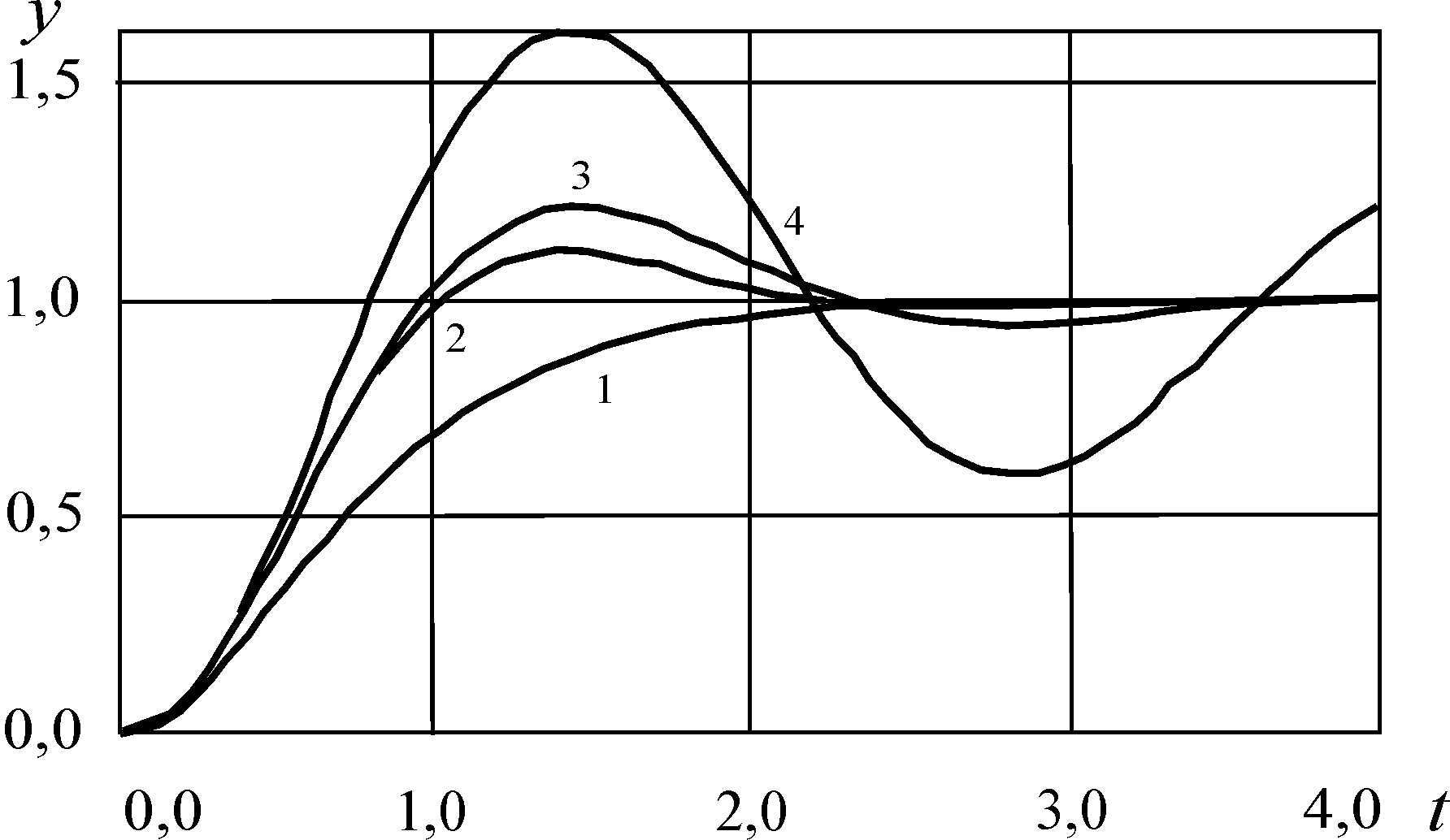
Рис. 6. Переходные процессы при различных схемах выбора эталона

Коэффициент усиления замкнутой системы

,

для всех указанных схем выбора эталона получился одинаковым

;

коэффициент модального регулятора найдется из условия обеспечения заданного коэффициента передачи:

.

Подставляя значения и в последнее выражение, окончательно получим .

Синтез модального регулятора полного порядка закончен.

Из последнего рисунка следует, что при использовании биномиальной схемы и схемы Баттерворта переходный процесс быстрее устанавливается, причем время сходимости примерно одинаковое, однако, во втором случае появляется перерегулирование. Время переходного процесса , что существенно превышает оценочное время переходного процесса . Наихудшие результаты получаются при использовании распределений, оптимальных по интегральным показателям качества (длительная сходимость и высокая колебательность).