2.1. Понятие о работе модели, управляемой событиями

Событие, не очень подходящее слово, слишком для этого значительное, в программировании означает, что в процессе выполнения программы может что-то произойти, то, что будет замечено и воспринято компьютером, и он сможет на это как-то отреагировать. Событием может быть щелчок кнопкой мышки, или то, что одна величина станет равной другой, например уровень воды в бассейне достигнет его верхней отметки и т.п. Если до того, как событие случилось, модель MVS действовала в соответствии с одними уравнениями, то после события модель можно подчинить другим уравнениям. Например, до включения крана уровень воды в бассейне был постоянным, а после “события” – включения крана, уровень воды возрастает пропорционально времени.

Событие нельзя заранее предугадать. В динамических моделях событие происходит в какой-то момент времени, привязано к нему. Статическая модель во времени не развивается, поэтому события в ней к моментам времени не привязаны.

Алгоритм поведения модели, управляемой событиями, может быть наглядно представлен графически. В программе MVS для этого служит Карта поведения. Это специальное окно, где можно графически изобразить и то, как модель мгновенно реагирует на события, и то, как она себя ведет, может быть достаточно длительное время, в промежутках между событиями. Наглядному представлению алгоритма помогают и окна, отображающие уравнения, которым подчиняется модель в промежутках между событиями.

Программа MVS позволяет пользователю строить модель, программировать ее поведение, используя две формы ее описания в карте поведения. Первая форма применяется в действиях переходов, во входных и выходных действиях узлов. Здесь пользователь может записывать мгновенные действия, которые должна будет выполнить модель, в виде операторов, похожих на те, которые используются, например, в языке Паскаль. Можно использовать операторы: присваивания, условный, цикла, вызова подпрограммы и др. (о правилах записи операторов см. справку в MVS). Фактическое время, затрачиваемое программой на выполнение операторов, не учитывается во времени функционирования модели. Для модели эти действия осуществляются мгновенно. Вторая форма описания поведения модели используется исключительно для описания непрерывного поведения модели в узле, т.е. здесь описывается то, как ведет себя модель с течением времени. Удобство этой формы заключается в том, что пользователь записывает уравнения, характеризующие поведение модели, в виде, близком к виду записи обычных математических уравнений. Т.о. здесь пользователю не приходится заботиться о составлении алгоритма решения уравнений и записи программы на алгоритмическом языке, MVS это делает сама. В совокупности, обе формы дают пользователю гибкий и удобный в использовании аппарат описания поведения моделей различной степени сложности.

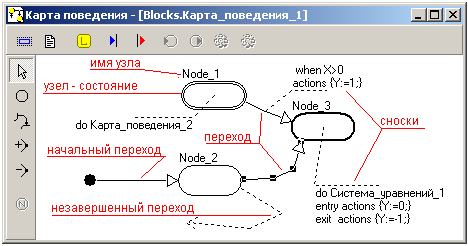
Рис. 2.2.3. Исходный вид главной карты поведения. Один узел Init в проекте имеется всегда и ему может быть приписано непрерывное во времени поведение модели в соответствии с уравнениями, называемыми Система_уравнений_1. Система уравнений вводится в специальном редакторе формул. Название системы уравнений может быть изменено и сделано соответствующим поведению модели в узле.

Узлы – это состояния.

Стрелки – переходы из состю. В сост.

Гибридный автомат – граф переходов из узла в узел

В программе MVS реализация и отображение алгоритмов, использующих управление событиями, осуществляется с помощью карты поведения модели. Узлы этой карты задают поведение модели в промежутках между событиями. События отображаются на карте направленными линиями, соединяющими узлы.

Имитационное моделирование является методом

моделирования объектов и процессов на ЭВМ. При

моделировании на ЭВМ вырабатывается информация,

описывающая элементарные явления исследуемого

процесса с учетом их связей и взаимных влияний.

Получаемая информация о состояниях процесса

используется для определения тех характеристик процесса,

которые нужно получить в результате моделирования.

Моделирующий алгоритм приближенно воспроизводит

реальный процесс во времени. Имитируются элементарные

явления, составляющие процесс, с сохранением их11

логической структуры и последовательности протекания во

времени. Моделирующий алгоритм позволяет по исходным

данным получить сведения о состоянии процесса в

произвольные моменты времени. Сущность имитационного

моделирования состоит в реализации на ЭВМ специального

алгоритма, который воспроизводит формализованный

процесс сложной системы.

Имитационное моделирование представляет собой

определенную последовательность этапов решения задач:

- изучение реальных систем;

- составление содержательного описания процесса

функционирования;

- формулировка цели исследования; выбор основных

критериев функционирования;

- разбиение сложной системы на подсистемы;

- построение формализованной схемы процесса

функционирования;

- построение математической модели системы;

- планирование эксперимента и сбор исходных данных;

-составление рабочей программы с учетом особенностей

машины;

- отладка программы;

- осуществление моделирования;

- обработка результатов;

- выработка рекомендаций

Сети петри:

Сети Петри - инструмент исследования систем. Сети Петри делают возможным моделирование системы математическим представлением ее в виде сети Петри. 

Виды сетей петри –

• Временная сеть Петри — переходы обладают весом, определяющим продолжительность срабатывания (задержку).

• Стохастическая сеть Петри — задержки являются случайными величинами.

• Функциональная сеть Петри — задержки определяются как функции некоторых аргументов, например, количества меток в каких-либо позициях, состояния некоторых переходов.

• Цветная сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.

• Ингибиторная сеть Петри — возможны ингибиторные дуги, запрещающие срабатывания перехода, если во входной позиции, связанной с переходом ингибиторной дугой, находится метка.

• Иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.

Основными свойствами сети Петри являются:

• ограниченность — число меток в любой позиции сети не может превысить некоторого значения K;

• безопасность — частный случай ограниченности, K=1;

• сохраняемость — постоянство загрузки ресурсов, 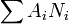  постоянна. Где 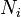  — число маркеров в i-той позиции, 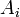  — весовой коэффициент;

• достижимость — возможность перехода сети из одного заданного состояния (характеризуемого распределением меток) в другое;

• живость — возможность срабатывания любого перехода при функционировании моделируемого объекта.

В основе исследования перечисленных свойств лежит анализ достижимости.

сеть Петри состоит из четырех элементов: множество позиций   (схематически обозначаются кружками), множества переходов   (обозначаются черточками), входной функции   и выходной функции  . Входная и выходная функции связаны с переходами и позициями. Входная функция   отображает переход   в множество позиций  , называемых входными позициями перехода. Выходная функция   отображает переход   в множество позиций  , называемыхвыходными позициями перехода. Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, а другие – от переходов к позициям.

Маркировка   - присвоение фишек позициям сети Петри. Фишка – примитивное понятие сетей Петри. Фишки используются для определениявыполнения сети Петри.

Выполнением сети Петри управляют количество и распределение фишек в сети. Фишки находятся в кружках (позициях) и управляют выполнением переходов сети. Сеть Петри выполняется посредством запуска переходов. Переход может запускаться только в том случае, когда он разрешен.

Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. 

30

 На этом шаге мы рассмотрим задачу о взаимном исключении. 

    Предположим, что несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Этот разделяемый элемент данных может использоваться процессами различными способами, упрощенно их можно классифицировать как чтение значения элемента данных или запись нового значения. Эти две операции являются часто единственными примитивными операциями. Это означает, что для обновления разделяемого элемента данных процесс должен сначала считать старое значение, затем вычислить новое, и записать его на то же место. Если два процесса в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть трудности. Возможна следующая последовательность:

1. Первый процесс считывает значение x из разделяемого объекта;

2. Второй процесс считывает значение x из разделяемого объекта;

3. Первый процесс вычисляет новое значение x' = f(x);

4. Второй процесс вычисляет новое значение x'' = g(x);

5. Первый процесс записывает x' в разделяемый объект;

6. Второй процесс записывает x'' в разделяемый объект, уничтожая значение x'.

    Результат вычисления первого процесса потерян, так как теперь значением разделяемого объекта является g(x), в то время, как им должно быть либо g(f(x)), либо f(g(x)).

    Для предотвращения проблем такого рода необходимо обеспечить механизм взаимного исключения. Взаимное исключение - это метод создания таких программ, что одновременно не более чем один процесс имеет доступ к разделяемому объекту данных. Участок кода, в котором осуществляется доступ к разделяемому объекту и который требует защиты от вмешательства других процессов, называется критической секцией. Идея состоит в том, что когда процесс готов выполнить свою критическую секцию, он сначала ждет, пока другой процесс не выполнит свою собственную критическую секцию. Затем он "блокирует" доступ к критической секции, не давая возможности никакому другому процессу войти в свою критическую секцию. Он входит в критическую секцию, выполняет ее и, выйдя из нее, освобождает ее для доступа со стороны других процессов.

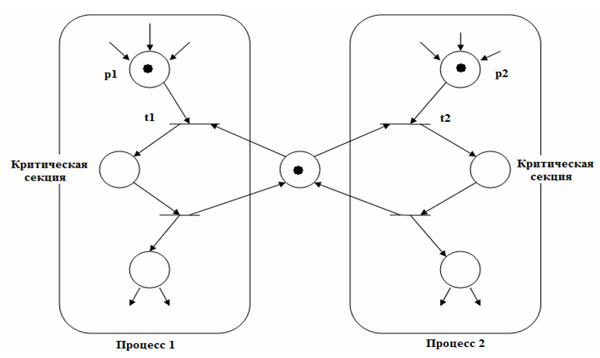Рис.1. Взаимное исключение

    Эта задача может быть решена сетью Петри, как показано на рисунке 1. Позиция m представляет собой разрешение для входа в критическую секцию. Для того, чтобы какой-либо процесс вошел в критическую секцию, он должен иметь фишку в p₁ или в p₂ соответственно, свидетельствующую о желании попасть в критическую секцию, а также должна существовать фишка в m, дающая разрешение на вход. Если оба процесса пытаются пройти в критическую секцию одновременно, то переходы t₁ и t₂ вступят в конфликт, и только один из них может запуститься. Запуск t₁ запретит переход t₂, вынуждая процесс 2 ждать, пока первый процесс выйдет из своей критической секции и возвратит фишку обратно в позицию m.

    На следующем шаге мы рассмотрим задачу о производителе/потребителе.