Вариант 7

ПН ПО	B1	B2	B3	B4	Запасы
A1	3	10	11	15	560
A2	22	11	4	2	420
A3	8	1	7	15	520
Потребности	300	380	450	370

Вариант 8

ПН ПО	B1	B2	B3	B4	Запасы
A1	11	4	15	7	250
A2	20	9	7	14	350
A3	18	9	3	8	300
Потребности	180	220	230	270

Вариант 9

ПН ПО	B1	B2	B3	B4	Запасы
A1	1	4	5	11	300
A2	12	8	3	14	320
A3	10	15	7	9	380
Потребности	250	200	290	260

Пример выполнения контрольной работы

Задача 1. Привести к жордановой форме, найти общее и базисное решение системы линейных уравнений

2x₁+3x₂+2x₃-10x₄=27

-2x₁+5x₂+2x₃-2x₄=9

-3x₁+4x₂-2x₃-x₄= -25

Решение.

Приведем систему к жордановой форме. Сделаем ведущим первое уравнение с базисной переменной X₁. Делаем коэффициент при X₁ равным 1, поделив уравнение на 2 , затем исключаем X₁ из второго и третьего уравнений. Получаем

x₁+3/2x₂+x₃-5x₄=27/2 (*2)+II; (*3)+III;

8x₂ + 4x₃-12x₄=36

17/2x₂ + x₃ -16x₄= 31/2

Теперь делаем ведущим второе уравнение с базисной переменной X₃.

x₁-1/2x₂ - 2x₄=9/2

2x₂ +x₃ -3x₄=9 *(-1)+I; *(-1)+III;

13/2x₂ + 13x₄= 13/2

Делаем ведущим третье уравнение с базисной переменной X₂:

x₁ - 3x₄ = 5

x₃ +x₄=7

x₂ - 2x₄= 1 (*1/2)+I; (*(-2))+II;

Жорданова форма получена. Общее решение:

x₁=5+3x₄

x₂=1+2x₄

x₃ =7- x₄

Базисное решение: x₁=5; x₂=1; x₃=7; x₄=0.

Задача 2. Решить геометрически задачу линейного программирования

f= 2x₁+3x₂ min

x₁-x₂>=1

3x₁-4x₂<=6

5x₁+7x₂<=28

Решение. Строим ОДР. Каждое из линейных неравенств геометрически представляет собой полуплоскость. ОДР является общей частью полуплоскостей.

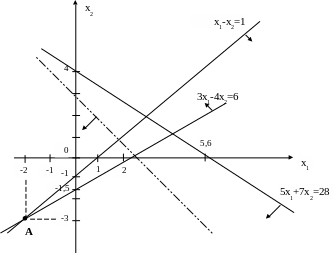
Строим линии уровня

2х₁+3х₂=C.

Отмечаем стрелкой направление,

в котором перемещается линия

уровня с уменьшением С. Видим,

что целевая функция достигает

минимума в точке А.

Для нахождения координат точки А решаем систему уравнений:

х₁-х₂=1 -3х₁+3х₂=-3

3х₁-4х₂=6 Имеем 3х₁-4х₂=6

-х₂=3; х₂= -3

х₁ =1+х₂= -2

Таким образом, оптимальное решение:

х₁= -2; х₂= -3; f_min= -13

Задача 3. Решить симплекс-методом задачу

f = 6x₁+7x₂ max

2x₁+3x₂<= 30

4x₁+2x₂<= 40

3x₁+4x₂<= 60

x₁ >=0,x₂>= 0.

Для решения ЗЛП симплекс – методом, приведем задачу к каноническому виду. Предварительно сократим второе неравенство на 2. Канонический вид задачи:

g=-f = -6x₁-7x₂ min

2x₁+3x₂+z₁=30

2x₁+x₂+z₂=20

3x₁+4x₂+z₃=60

x₁>=0, x₂>=0, z₁>=0, z₂ >=0, z₃>=0.

Перед заполнением симплекс – таблицы задачу нужно привести к табличному виду. Для этого целевую функцию записываем так:

g+6x₁+7x₂=0.

Заполняем симплекс – таблицу:

Б	X1	X2	Z1	Z2	Z3	Q
Z1	2	3	1	0	0	30
Z2	2	1	0	1	0	20
Z3	3	4	0	0	1	60
g	6	7	0	0	0	0

Условия оптимальности и неразрешимости не выполняются. Приступаем к выбору генерального элемента. В качестве генерального столбца выбираем второй столбец. Затем составляем отношения 30:3, 20:1, 60:4. Первую строку, для которой это отношение наименьшее, выбираем в качестве генеральной. Затем базисную переменную z₁ заменяем на x₂ и с помощью жордановой процедуры заполняем следующую симплекс – таблицу. Так продолжаем до тех пор, пока не будет достигнуто условие оптимальности.

Б	X1	X2	Z1	Z2	Z3	Q
Z1	2/3	1	1/3	0	0	10
Z2	4/3	0	-1/3	1	0	10
Z3	5/3	0	-4/3	0	1	20
g	4/3	0	-7/3	0	0	-70

Б	X1	X2	Z1	Z2	Z3	Q
Z1	0	1	1/2	-1/2	0	5
Z2	1	0	-1/4	3/4	0	15/2
Z3	0	0	-11/12	-5/4	1	15/2
g	0	0	-2	-1	0	-80

План оптимален. Он имеет вид:

x₂=5; x₁=15/2; z₃=15/2; z₁=0; z₂=0; g_min=-80.

Возвращаясь к исходной постановке, имеем следующий оптимальный план:

x₁=7,5; x₂=5; f_max = 80.

Задача 4. Найти оптимальное решение ЗЛП, перейдя к двойственной задаче, и решив последнюю геометрически

f=x₁-2x₂+3x₃-x₄ max

2x₁-x₂+2x₃-3x₄<=5

x₁+2x₂-x₃+x₄<=3

x_j>=0 (J=1,2,3,4)

Решение. Запишем двойственную задачу

= 5y₁+3y₂ min

2y₁+y₂>=1

-y₁+y₂>= -2

2y₁- y₂>=3

-3y₁+y₂>=-1

y₁>=0, y₂>=0

Решим двойственную задачу геометрически.

Построим ОДР. Для этого строим полуплоскости, определяемые каждым из неравенств, затем ищем общую часть этих полуплоскостей.

В нашем случае ОДР пуста. Следовательно, двойственная задача неразрешима. По первой теореме двойственности неразрешимой является и прямая задача.

Задача 5. Решить транспортную задачу, исходящие данные которой заданы таблицей

ПН ПО	B1	B2	B3	Запасы
A1	2	4	3	38
A2	7	5	2	92
A3	8	3	4	50
Потребности	80	20	40

Это – открытая транспортная задача, так как сумма запасов равна 180, а сумма потребностей – 140. Поэтому нужно добавить фиктивный пункт назначения с потребностью 40.

Получим таблицу:

пн по	B1	B2	B3	B4	Запасы
A1	2	4	3	0	38
A2	7	5	2	0	92
A3	8	3	4	0	50
Потребности	80	20	40	40

Найдем исходный опорный план перевозок, к примеру, методом северо – западного угла, построим систему потенциалов и рассчитаем псевдостоимости свободных клеток:

пн по	B1	B2	B3	B4	Запасы	i
A1	38 2	0 4	-3 3	-7 0	38	0
A2	42 7	20 5	30 2	-2 0	92	5
A3	9 8	7 3	10 4	40 0	50	7
Потребности	80	20	40	40
j	2	0	-3	-7

В клетке (А₃,В₂) псевдостоимость больше стоимости, строим цикл пересчета, проходящий через эту клетку, делаем по нему максимальный допустимый сдвиг, равный 10. Получим новый план перевозок, с которым проделываем то же самое, что и с предыдущим опорным планом.

пн по	B1	B2	B3	B4	Запасы	i
A1	38 2	0 4	-3 3	-3 0	38	0
A2	42 7	10 5	40 2	2 0	92	5
A3	5 8	10 3	0 4	40 0	50	3
Потребности	80	20	40	40
j	2	0	-3	-3

Строим новую таблицу и продолжаем процедуру.

пн по	B1	B2	B3	B4	Запасы	i
A1	38 2	-2 4	-3 3	-5 0	38	0
A2	42 7	3 5	40 2	10 0	92	5
A3	7 8	20 3	2 4	30 0	50	5
Потребности	80	20	40	40
j	2	-2	-3	-5

План оптимален, так как в каждой клетке псевдостоимость не больше стоимости. Опустив фиктивный пункт В₄, получим следующий оптимальный план перевозок для исходной задачи.

пн по	B1	B2	B3	Запасы
A1	38 2	4	3	38
A2	42 7	5	40 2	92
A3	8	20 3	4	50
Потребности	80	20	40

Вычислим стоимость перевозок:

f_min=38*2+42*7+20*3+40*2=510 ден. ед.