11 Лекция 11. Помехоустойчивые корректирующие коды.

Цель лекции: ознакомление c помехоустойчивыми корректирующими кодами.

Содержание:

а) общие сведения;

б) Блоковые коды;

в) избыточность сообщений;

г) связь корректирующей способности кода с кодовым расстоянием.

11.1. Общие сведения.

Необходимость введения избыточности.

Причем избыточность вводится, чтобы вводимые разряды удовлетворяли дополнительным условиям, проверка этих условий дает возможность обнаружить и исправить ошибки. Такие коды называются помехоустойчивые корректирующие коды и используются для обнаружения и исправления ошибок.

Обнаруживающие - коды которые обнаруживают ошибки.

В большинстве своем п/у коды являются алгебраическими т.е. результат проверки осуществляется в ходе выполнения над элементами кода алгебраических действий.

Алгебраические коды делятся:

Блоковые;

Неравномерные;

Блоковые коды имеют четкое деление на блоки, в пределах которых последовательности из R информационных символов ставятся в соответствие m контрольных: n=k+m

Блоковые коды могут быть равномерные, неравномерные если n=const.

Различают:

Разделимые – четкое деление на k и m символы

Неразделимые - нет деления на k и m символы (требуется в криптографии)

Неравномерные коды. В отличие от блоковых избыточность вводится непрерывно без разделения последовательности на блоки.

Могут быть:

Разделимыми;

Неразделимыми.

Пример непрерывного кода - реккурент (сверточно)

11.2 Блоковые коды

11.2.1. Общие принципы использования избыточности

Способность кода обнаружить и исправить ошибки обусловлено наличием избыточных символов.

Обнаружение ошибок. Рассмотрим последовательность информационных символов, поступивших на вход кодирующего устройства на выходе КУ каждому блоку из k символов ставится в соответствие блок из n символов.

В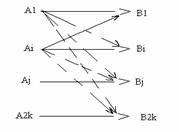 озможно вычислить: - безошибочная передача;

-переход в другие разряды КК (необн. ош.);

-переход в неразр. КК (обн. ошибка);

Следовательно, часть обнаруженных КК от общего числа возможных случаев равна:

В пределе : k=n -> Kобн =0

Допустим: n =k+1 т.е. имеется всего один избыточный символ тогда:

Тогда будет обнаружено половина всех ошибок.

Исправление ошибок.

При декодировании необходимо полученные КК разбить на непересекающихся множества М, каждое из которых ставится в соответствие одной из разрешенных КК. При получении какой либо КК, В – принадлежит множеству М мы примем ее как передаваемая кодовая комбинация А, ошибка может быть исправлена в случаях.

Всего случаев перехода в неразрешенные комбинации КК:

т.е. при наличии избыточности код способен исправлять ошибки:

Чем больше контрольных символов, тем меньше возможность их исправить. Способ разбиения на множества зависит от характеристик кода. Большинство помехоустойчивых кодов разработаны для исправления взаимно независимых ошибок и исправления пакетов ошибок.

Взаимно независимые ошибки зависят от текущих искажений и не зависят от предыстории.

При взаимно независимых ошибках вероятность искажения любых r символов в n – разрядной КК: – вероятность ошибки.

Т.к. p<<1 , то наиболее вероятны ошибки низшей кратности.