8.2 Временное, спектральное и векторное представление сигналов

АМ и ЧМ

Временная диаграмма АМ сигнала показана на рисунке 7.2.

Спектральная диаграмма однотонального АМ сигнала, построенная по

(8.3)

симметричной относительно несущей частоты (рисунок 8.2). Амплитуды боковых колебаний одинаковы и даже при М=1 не превышают половины амплитуды несущего колебания А₀.

Рисунок 8.2 - Спектральная диаграмма АМ сигнала при

однотональной модуляции

При гармоническом несущем сигнале временная диаграмма ЧМ:

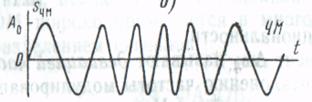
Рисунок 8.3

Спектральная диаграмма ЧМ сигнала:

Рисунок 8.4

Векторные диаграммы АМ и ЧМ представлены на рисунке 8.5.

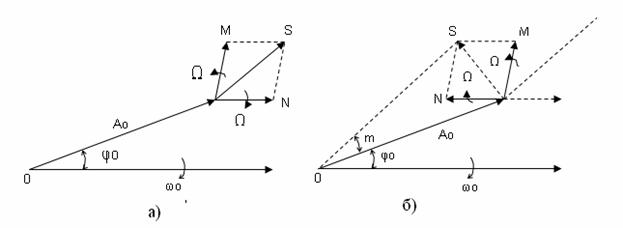
Рисунок 8.5 - АМ сигнал (а), ЧМ сигнал (б)

8.3 Ширина полосы частот и различие в спектрах чм и фм сигналов

При однотональной модуляции

Отсюда следует, что спектры ФМ и ЧМ одинаковы, если m_ЧМ= m_ФМ= m, поэтому будем рассматривать один из них, например ЧМ, для упрощения записей ψ₀=0 и Ψ=0.

Для построения спектральной диаграммы ЧМ необходимо знание функций Бесселя J_k(m) при различных значениях k и m. Их можно найти в математических справочниках. На рис 8.6 приведены графики функций Бесселя при k, m≤8. Значения функций Бесселя, не отображенных на графике можно найти по формуле

J_k+1(m)=(2k/m) J_k(m)- J_k-1(m)

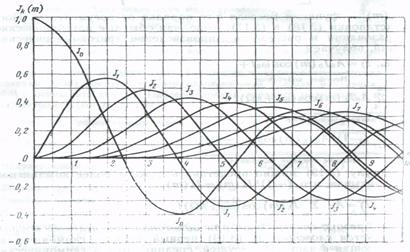
Рисунок 8.6 - Графики функций Бессаля

Из графиков функции Бесселя следует интересная закономерность: чем больше порядок k функции Бесселя, тем при больших аргументах m наблюдается её максимум, однако при k >m значения функций Бесселя оказывается малой величиной. А раз так, то малыми будут и составляющие спектра и ими можно пренебречь. В практике считают, что можно пренебречь всеми спектральными составляющими, номера которых k >m+1 (уровень меньше 5% от уровня несущей). Отсюда следует что ширина спектра сигнала

∆f_ЧМ,ФМ≈2(m+1)F_M (8.4)

где F_M=Ω/2π – частота модулирующего сигнала. Для передачи модулированного сигнала с высокой точностью иногда считают, что надо учитывать спектральные составляющие с уровнем не менее 1% от уровня несущей. Тогда ширина спектра с угловой модуляцией (рисунок 6.4)

∆f_ЧМ,ФМ≈2(m+ +1)F_M

Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции Ω. При ЧМ , поэтому при m>>1 полоса практически не зависит от F_m. При ФМ и при m>>1 ширина спектра будет равна , т.е. она зависит от модулирующей частоты F_m. В этом и состоит различие в спектрах ЧМ и ФМ. В случае малого индекса модулирующий спектр ЧМ и ФМ сигналов, так же как и в случае АМ, имеет только три составляющие:

(8.5)

9 Лекция 9. Импульсная модуляция.

Цель лекции: ознакомление с применением импульсной техники для передачи сигналов, импульсная модуляция, амплитудно - импульсная модуляция (АИМ), широтно-имульсная модуляция(ШИМ), фазо-импульсная модуляция(ФИМ), их характеристики.

Содержание:

а) Применение импульсной техники для передачи сигналов, импульсная модуляция, амплитудно - импульсная модуляция (АИМ), широтно-имульсная модуляция(ШИМ), фазо-импульсная модуляция(ФИМ), их характеристики;

б) методы дискретной модуляции;

в) спектр импульсных последовательностей.

9.1 Применение импульсной техники для передачи сигналов, импульсная модуляция, амплитудно - импульсная модуляция (АИМ), широтно-имульсная модуляция(ШИМ), фазо-импульсная модуляция(ФИМ), их характеристики

В системах с импульсной модуляцией переносчиком информации служит периодическая последовательность импульсов одинаковой формы

(9.1)

где U(t) – нормированная функция, характеризующая форму импульса; А_о – амплитуда импульса; t_k – начало переднего импульса k – го импульса t_k=kT_i+t_o; T_i – период следования импульсов; t_о – начало отсчета последовательности; τ_k – длительность k – го импульса, отсчитываемая на некотором заданном уровне.

При модуляции один из параметров последовательности изменяется в соответствии с передаваемым сообщением .

При амплитудно – импульсной модуляции (АИМ) изменяется амплитуда импульса А:

. (9.2)

При широтно-имульсной модуляции (ШИМ) изменяется длительность импульса:

(9.3)

где - максимальное отклонение фронта импульсов в одну сторону.

При фазо-импульсной модуляции(ФИМ) изменяется сдвиг импульсов относительно тактовых точек :

. (9.4)

Р исунок 9.1 - Сигналы при различных видах импульсной модуляции