7.3 Амплитудная (ам), частотная(чм), фазовая(фм) модуляции

7.3.1 Амплитудная модуляция

При амплитудной модуляции амплитуда несущего колебания изменяется пропорционально мгновенным значениям модулирующего сигнала u_m(t), то есть получает приращение и становится равной:

(7.4)

Где А₀ – амплитуда несущей; а – коэффициент пропорциональности, выбираемый так, чтобы амплитуда А(t) всегда была положительной. Частота и фаза несущего гармонического колебания при АМ остаются неизменными.

Временная диаграмма АМ сигнала показана на рис. 5.2, из которого видно, что в соответствии с мгновенными значениями u_m(t) амплитуда несущей А_о увеличивается до значения A_{m max} получая приращения , то уменьшается до A_min, получая приращение . Обращает на себя внимание, что амплитуда А(t) повторяет форму модулирующего сигнала u_m(t). В АМ сигнале амплитуда А(t) является огибающей высокочастотного заполнения (на рис.7.2,б она изображена штриховой линией).

Рисунок 7.2 - Амплитудно – модулированный сигнал:

а ) модулирующий сигнал u_m(t);

б) АМ сигнал

Коэффициент модуляции:

. (7.5)

Математическая модель:

. (7.6)

7.3.2 Частотная модуляция

При частотной модуляции отклонение частоты модулированного сигнала от ω_о изменяется пропорционально мгновенным значениям модулирующего сигнала u_m(t):

. (7.7)

где ∆ω_Д –коэффициент пропорциональности

∆ω_Д называют девиацией частоты и она равна наибольшему отклонению частоты несущей ω₀. Изменение частоты ЧМ сигнала графически показано на рис. 7.3 , где отмечена девиация частоты ∆ω_Д, соответствующая наибольшему отклонению частоты вниз ∆ω_Д=∆ω_-, поскольку ∆ω₊ <∆ω_. Величина u_m(t) нормирована, то есть | u_m(t)|≤1.

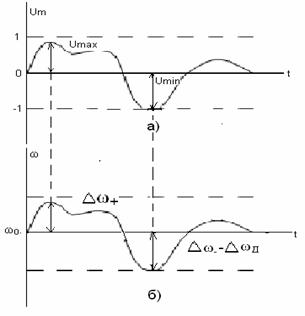
Рисунок 7.3 - Мгновенная частота ЧМ сигнала:

а) модулирующий сигнал;

б) изменение мгновенной частоты

Девиация частоты является одним из важных параметров частотных модуляторов и может принимать значения от единиц герц до сотен мегагерц в модуляторах различного назначения. Однако, всегда необходимо чтобы выполнялось условие << .

Полную фазу ЧМ сигнала с частотой (8.7) находим путем интегрирования , т.е.

где ψ_о можно рассматривать как постоянную интегрирования.

Тогда аналитическое выражение (математическая модель) ЧМ сигнала запишется в виде

. (7.8)

Поскольку u_m(t) входит в это выражение под знаком интеграла, ЧМ часто называют интегральным видом модуляции.

8 Лекция 8. Фазовая модуляция.

Цель лекции: ознакомление с фазовой модуляцией информации и временным, спектральным, векторным представлением сигналов АМ и ЧМ.

Содержание:

а) фазовая модуляция носителей информации;

б) временное, спектральное и векторное представление сигналов

АМ и ЧМ.

8.1 Фазовая модуляция

При фазовой модуляции, отклонение (сдвиг) фазы модулированного сигнала от линейной ω₀t+ψ₀ изменяется пропорционально мгновенным значениям модулирующего сигнала u_m(t)

. (8.9)

Где - коэффициент пропорциональности, называемый девиацией фазы. Физический смысл этого коэффициента поясняется рис.8.1, где изображены модулирующий сигнал и полная фаза ФМ сигнала. С увеличением сигнала u_m(t) полная фаза растет во времени быстрее, чем по линейному закону. При значениях сигнала u_m(t)<0 происходит спад скорости роста . Абсолютная величина отклонения (сдвига) фазы от линейной наибольшая, когда u_m(t) достигает экстремальных значений. На рис 8.1,б отмечено максимальное отклонение фазы вверх и вниз . Наибольшее отклонение фазы от линейной и является девиацией фазы . Измеряется в радианах и может принимать значение от единиц до десятков тысяч радиан.

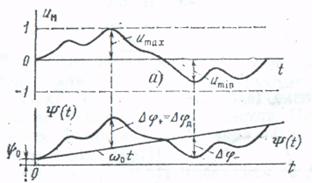
б)

Рисунок 8.1 - Полная фаза ФМ сигнала:

а) модулирующий сигнал;

б) изменение полной фазы

Математическая модель:

(8.2)