6.3 Теорема Котельникова (Основная теорема Шеннона)

Согласно теореме В.А.Котельникова любой сигнал u(t), не содержащий частоты выше F_m , можно точно восстановить по его отсчетам u(k∆t), взятым через интервалы ∆t=1/2F_m. Восстановление сигнала осуществляется с помощью ряда

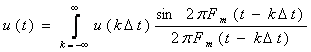. (6.11)

Ряд, определяемый выражением (6.11), называется рядом Котельникова. В нём коэффициенты разложения u(k∆t), равные мгновенным значениям непрерывного сигнала u(t) в моменты k∆t, являются отсчетами сигнала u(t), а функции

(6.12)

Эти функциями отсчетов, которые имеют одинаковую форму функции типа sinx/x и отличаются друг от друга временным сдвигом на интервал k∆t. Графики функции и их особые (максимумы, минимумы, пересечения с осями координат) показаны на рис. 6.1. Функции отсчетов представляют собой импульсную реакцию идеального ФНЧ с граничной частотой F_m , если на его вход подавать δ –функцию в момент k∆t.

Теорема Котельникова является основой для дискретизации непрерывных сигналов по времени, так как, во-первых, доказывает, что непрерывный сигнал можно заменить его дискретными значениями, во-вторых, даёт правило вычисления шага дискретизации ∆t=1/2F_m . При таком шаге дискретизации ряд Котельникова даёт точное временное представление сложного сигнала.

6.4 Пропускная способность непрерывного канала (без помех и с помехами)

Среднее количество информации , передаваемое сигналом на интервале Т:

H_T(s) и H_T(s/x) – энтропии. (6.13)

Скорость передачи информации по непрерывному каналу находится как предел:

. (6.14)

Максимальная скорость передачи в непрерывном канале определяет его пропускную способность

(6.15)

где максимум определяется по всем возможным ансамблям входных сигналов s.

Вычислим пропускную способность непрерывного канала, в котором помехой является аддитивный шум ω(t), представляющий собой случайный эргодический процесс с нормальным распределением и равномерным спектром. Средние мощности сигнала и шума ограничины величинами Р_с и Р_ш, а ширина их спектра равна F.

Условная энтропия H_T(x/s) при аддитивном шуме зависит только от его распределения р_ш(ω), что и объясняет термин энтропия шума. На интервале Т.

( 6.16)

где n = 2FT.

Значения шума с равномерным спектром некоррелированы между собой в моменты отсчетов, разделенные интервалом Δt=1/2F. Отсутствие представить энтропию суммы n отсчетов шума (6.16) как сумму энтропий отдельных отсчетов, которые вследствие стационарности шума равны между собой. С учетом этих соображений можно записать

H_T(ω)=nH(ω)=2FTH(ω) . (6.17)

При данной величине H_T(x/s)=H_T(ω) пропускная способность отыскивается путем максимизации. Отсюда . (6.18)

Здесь предполагается, что сигнал s и помеха ω независимы, поэтому мощность сигнала x равна сумме мощностей Р_с+Р_ш. Тогда

. (6.19)

6.5 Модель нкс

Канал может быть представлен цепью с соответствующей импульсной характеристикой и источниками помех.

В канале всегда присутствуют аддитивные гауссовские помехи. Кроме гаусcовских в канале действуют помехи:

 гармонические (сосредоточенные по частоте);

 импульсные (сосредоточенные по времени);

 мультипликативные;

 перерывы связи (17,4 дБ).

К искажениям формы сигнала, также приводят:

 сдвиг частотных составляющих по частоте;

 фазовые скачки;

 фазовое дрожание.

Упрощенная модель канала представлена на следующем рисунке

Рисунок 6.2

На входе и выходе непрерывный канал связи– непрерывный сигнал, непрерывного времени.