
- •Коммерциялық емес акционерлік қоғам
- •Ақпараттар теориясы
- •5В070400 – «Есептеу техникасы және бағдарламамен қамтамасыз ету» мамандығының барлық оқу бөлімінің студенттері үшін дәрістер жинағы
- •1 Дәріс. Сигнал, ақпарат және хабар
- •1.1 Хабар кездейсоқ үрдіс ретінде
- •1.2 Детерминделген сигналдарды бейнелеу формалары
- •1.1 Сурет - Сигналдардың бейнелеу формулалары
- •1.3 Хартли өлшемі. Ақпараттың сандық бағасы
- •1.4 Шеннон энтропиясы мен Больцман энтропиясының арасындағы байланыс
- •1.2 Сурет - Ықтималдылықты жағдайлардың айырмашылығы
- •1.4 Ақпарат түсінігі
- •2 Дәріс. Бөгеусіз дискретті арна
- •2.1 Ақпарат таратудың бөгеусіз дискретті арнасы
- •2.2 Арнаның өткізу қабілеті
- •2.3 Бөгеусіз арнаның өткізу қабілеті үшін теорема
- •2.4 Бөгеусіз дискретті арнаның математикалық моделі
- •2.1 Сурет - Екілік симметриялық арнадағы өту ықтималдығы
- •3 Дәріс. Бөгеулері бар дискретті арна
- •3.1 Бөгеу туралы ұғым
- •3.2 Бөгеулердің түрлері
- •3.3 Бөгеулі ақпаратты таратушы дискретті арна
- •3.1 Сурет - Екілік арнаның өткізгіштілік қабілетінің қателік мүмкіндігіне р0 қатынасы
- •4 Дәріс. Бөгеулері бар дискретті арна (жалғасы)
- •4.1 Кедергісі және өткізгіштік қабілеті бар арнаға арналған теорема
- •4.2 Бөгеулі дискреттік арналардының математикалық моделі
- •4.3 Ақпаратты үздіксіз түрде ұсыну
- •4.1 Сурет - Сигналдың түрлері
- •4.4 Сигналды қалпына келтіру сапасының критерилері
- •5 Дәріс. Үздіксіз арна
- •5.1 Үздіксіз сигналды ортогональды қатарларға жіктеу
- •5.2 Фурье қатарлары және олардың байланыс техникасында қолданылуы
- •5.3 Котельников теоремасы (Шеннонның негізгі теоремасы)
- •5.4 Үздіксіз арнаның өткізу қабілеті (бөгеусіз және бөгеулермен)
- •5.1 Сурет - үб арнасының үлгісі
- •6 Дәріс. Байланыс жүйесіндегі сигналдарды түрлендіру және қалыптастыру әдістері
- •6.1 Ақпарат тасушының модуляциялау әдістері
- •6.2 Гармоникалық модуляциялық сигналы
- •6.1 Сурет - Модулятор
- •6.3 Амплитудалық (ам), жиіліктік (чм), фазалық (фм) модуляция
- •6.2 Сурет - Амплитудалық – модуляцияланған сигнал
- •6.3 Сурет – Жм сигналының лездік жиілігі
- •7 Дәріс. Фазалық модуляция
- •7.1 Фазалық модуляция
- •7.2 Сигналдардың уақыттық, спектрлік және векторлық көріністері
- •7.4 Жиілік жолығының ұзындығы және жм және фм сигналдарының спектрлерінің айырмашылығы.
- •7.6 Сурет - Бессель функцияларының графиктері
- •8 Дәріс. Импульсті модуляция
- •8.1 Сурет – Әр түрлі импульсті модуляция сигналдары
- •8.2 Дискреттік модуляциялау әдістері
- •8.2 Сурет - Дискреттік модуляция кезіндегі сигналдардың уақыттық диаграммалары
- •8.3. Импульстер жүйесінің спектрі
- •8.3 Сурет - Импульстер жүйесінің спектрі
- •9 Дәріс. Бөгеуге тұрақты кодтау теориясы
- •9.1 Өткізгіштік қабілеті және құжаттарды жіберу жылдамдығы
- •9.2 Мәліметтердің артықшылығы
- •9.3 Тиімді кодтау теоремасы
- •10 Дәріс. Бөгеуге тұрақты түзетуші кодтар
- •10.1 Жалпы мәліметтер
- •10.2 Қателерді табудың және түзетудің негізгі принциптері
- •10.3 Кодалық қашықтық және кодтың түзету қабілеті
- •10.4 Кодтарды түзету классификациясы
- •11 Дәріс. Бөгеуге тұрақты түзетуші кодтар (жалғасы)
- •11.2 Үйірткі кодтар
- •12 Дәріс. Жүйелердің бөгеулерге тұрақтылық теориясы
- •12.1 Хабарлардың оптималды қабылдау шарттары
- •12.2 Оптималды қабылдағыштардың алгоритмдер мен сұлбаларын синтездеу, коррелияцилық қабылдағыш, үйлестірілген сүзгісі бар қабылдағыш
- •12.1 Сурет - Котельниковтың қолайлы қабылдағышы
- •13 Дәріс. Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Сурет - Котельников үйлесімді сүзгілі оптималды қабылдағышы
- •13.2 Модуляция түрлері және сигналды қабылдаудың әртүрлі
- •13.2 Сурет – ам, жм, фм сигналдарының эквивалентті энергияларын анықтау үшін
- •13.2 Салыстырмалы фазо-манипуляцияланған сигналдар
- •14 Дәріс. Көпарналы байланыс
- •14.1 Көпарналы байланыс
- •14.1 Сурет- Көпарналы байланыс арнасынын функционалды сұлбасы
- •14.2 Сигналдардың фазалық, жиіліктік, уақыттық бөлінуінің әдістері
- •14.2 Сурет - Арналардың уақытша бөлінуі
- •14.3 Сурет - цат-тің құрылымдық сұлбасы
- •15 Дәріс. Модуляцияның цифрлық әдістері
- •15.1 Ақпаратты қалпына келтіру және дискритизацияның принципі
- •15.1 Сурет - Аналогтық сигналдың цифрлық икм сигналға айналу құрылымы
- •15.2 Импулсті - кодалық модуляция (икм)
- •Мазмұны
5.1 Үздіксіз сигналды ортогональды қатарларға жіктеу
Байланыс теориясында сигналдар ұсынуылуы үшін функциялардың ортогональды қатарларға жіктелудің 2 дербес түрі кең қолданылады: тригонометриялық функциялар бойынша жіктелу және sin x/x түріндегі функциялар бойынша жіктелу. Бірінші жағдайда сигналдың әдеттегі Фурье қатары түріндегі спектрін, ал екінші жағдайда – Котельников қатар түріндегі уақыт бойынша көрінісін аламыз.
Сигналдың қолданбалы жағынан қарапайым берілуі – кейбір элементарлық функциялардың сызықтық комбинациясы.
![]() .
(5.1)
.
(5.1)
Жалпы жағдайда, сигнал – күрделі тербеліс, сондықтан сигналды анықтайтын s(t) күрделі функциясын қарапайым функциялар арқылы көрсету қажет.
Сызықтық жүйелерді зерттегенде сигналдың осындай берілуі өте ыңғайлы. Ол суперпозиция принцибын қолданып, көптеген есептерді бөлімдерге бөлуге мүмкіндік береді. Мысалы, сызықтық жүйенің шығысында сигналды анықтау үшін, жүйенің әрбір элементарлы әсерге реакциясы ψk(t) есептеледі, ал содан соң аk сәйкес коэффициенттеріне көбейтілген нәтижелер жеңіл есептелінеді және сома мүшелерінің санына тәуелді болмайды. Көрсетілген талаптарды ең толық ортогональды функциялардың жиынтығы қанағаттандырады.
Егер
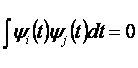 ,
,
![]() .
(5.2)
.
(5.2)
![]()
![]() аралықта
берілсе, онда
аралықта
берілсе, онда
![]() функциялары
ортогональды деп аталады.
функциялары
ортогональды деп аталады.
5.2 Фурье қатарлары және олардың байланыс техникасында қолданылуы
Сигналдардың спектрлік анализының негізі уақыт функциялардың қатар немесе Фурье интегралы түрінде берілуі. Кез келген периодты Дирихле қатарын қанағаттандыратын s(t) сигналы, тригонометриялық қатар түрінде көрсетілуі мүмкін
![]() мұнда
мұнда
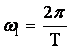 ,
(5.3)
,
(5.3)
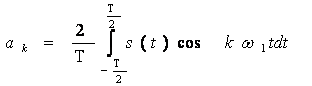 ,
(5.4)
,
(5.4)
 .
(5.5)
.
(5.5)
а0 өлшемі бір периодтағы сигналдың орташа мәнін көрсетеді және ол тұрақты құраушы деп аталады. Мына формула бойынша есептелінеді:
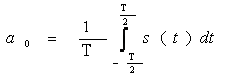 .
(5.6)
.
(5.6)
Бұл формуланы комплексті түрде Фурье қатарына салып көрсетсек:
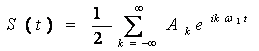 ,
(5.7)
,
(5.7)
мұнда
![]() ,
,
![]()
![]() .
.
Ak өлшемі комплексті амплитуда, ол мына формула бойынша табылады
 .
(5.8)
.
(5.8)
(5.7) және (5.8) формулалар Фурье қатарының дискретті құраушысын көрсетеді. Фурье қатарында тек периодтық сигналды ғана емес сонымен қатар басқа да сигналды көрсетуге болады. Соңғы жағдайда S(t) сигналы уақыт осінде периодты болып қабылданады. Мұнда (5.4) немесе (5.8) теңдігі мына (-Т/2,Т/2) ұзақтық интервалдағы сигналды көрсетеді. Кездейсоқ сигнал (немесе шуыл) (-Т/2,Т/2) интервалында берілген болса, онда ол Фурье қатарымен:
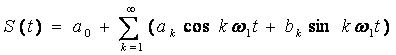 ,
(5.9)
,
(5.9)
мұнда ak және bk кездейсоқ өлшем болып табылады (флуктуациялық шуылда – тәуелсіз кездейсоқ нормалды таралу).
5.3 Котельников теоремасы (Шеннонның негізгі теоремасы)
В.А.Котельников теоремасына сәйкес жиілігі Fm нен аспайтын әр түрлі u(t) сигналын, ∆t=1/2Fm қадамымен алынған u(k∆t)санағымен қалпына келтіруге болады. Сигналды қалпына келтіру келесі теңдікпен жүзеге асады:
 .
(5.10)
.
(5.10)
(5.11) теңдігімен анықталатын қатарды Котельников қатары дейміз. Мұндағы k∆t мезетіндегі u(t) үзіліссіз сигналдың лездік мәндеріне тең болатын u(k∆t) жіктеу коэффициентін u(t) сигналының есеп берулері болып табылады, ал функциялары:
![]() (5.11)
(5.11)
Бұл
есеп берулердің функциялары
sinx/х функция
түрлері сияқты бірдей формалары бар
және бір бірінен интервалы k∆t
болатын уақыттық жылжулармен ерекшеленеді.
![]() функциясының
графиктері және олардың ерекшелері
(максимумдары, минимумдары, координаттар
осімен қиылысулары) 5.1 суретінде
көрсетілген. Егер k∆t
мезетінде кірісіне δ
–функциясын
берсек,
есеп
беру функциялары Fm
шекаралық жиілігі бар идеалды ТЖС-ның
импульсты реакцияларын көрсетеді.
функциясының
графиктері және олардың ерекшелері
(максимумдары, минимумдары, координаттар
осімен қиылысулары) 5.1 суретінде
көрсетілген. Егер k∆t
мезетінде кірісіне δ
–функциясын
берсек,
есеп
беру функциялары Fm
шекаралық жиілігі бар идеалды ТЖС-ның
импульсты реакцияларын көрсетеді.
Котельников теоремасы үзіліссіз сигналдарды уақыт бойынша дискреттеудің негізі болып табылады. Өйткені, біріншіден үзіліссіз сигналды оның дискретті мәндерімен алмастыра алатынымызды дәлелдейді, екіншіден дискреттеу қадамын өлшеу заңдылығын береді ∆t=1/2Fm. Осы дискреттеу қадамы арқылы Котельников теоремасы күрделі сигналдың уақыт түсінігін нақтылап береді.
