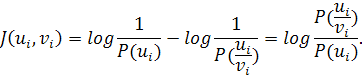3.3 Бөгеулі ақпаратты таратушы дискретті арна

Әртүрлі кедергілері бар арналарда бөгеулер басқа орын алады. Олардың берілетің сигналға әсері хабар көзінен шығатын ақпаратты жоғалту мен бүлінуіне әкеліп соғады. Кедергілермен арнасында қабылданған _I сигналына берілген бір немесе бірнеше u сигналы сәйкес келуі мүмкін. Бұнда u және арасындағы сәйкестік кездейсоқ сипатта, сондықтан белгісіздік дәрежесі P(u_i/ _i) шартты апостериоралдық мүмкіндігімен сипатталады да, P(u_i/ _i) <1 әрқашан болады. Қалған белгісіздікті log 1/P(u_i/3_i) жою үшін ақпараттын мөлшері, сол ақпараттың бөлігіне тең екені анық және айырым ретінде анықталады:

(3.1)

Кедергілермен арнаның өткізгіштік қабілеті берілген шектеулер кезінде берілетің сигналдарға қойылатың мүмкін болатын таратудың максималды жылдамдығы:

(3.2)

τ -ға тең ұзақтығы бірдей арналарға арналған өткізгіштік қабілеті

, (3.3)

u , Р барлық мүмкін болатын сигналдар ансамбілі арқылы максимум ізделеді.

Дискретті сигналдар берілетін ансамбілден таңдалған априордық мүмкіндіктері Р(u₁) және Р(u₂) екі тәуелсіз сигналы u₁ және u₂ бар кедергілерімен жадысыз екілік арнаны қарастырайық. Дұрыс қабылдағанда сәйкесінше u₁ және u₂ шығаратың арнаның шығысында υ₁ және υ₂ сигналдар қалыптасады. Кедергілер әрекеті кезінде u₁ тарату кезіңде Р(υ_2/u₁) мүмкіндігімен, u₂ кезінде Р(υ_1/ u₂) болатын сипатталатын қателіктер болуы мүмкін.

Сигналдың энтропиясын табайық:

. (3.4)

Және шу энетропиясын:

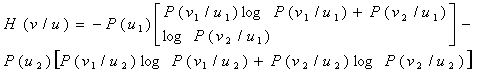(3.5)

Арнаны симметриялы деп қарастырайық. Ондай арналарға ауысу мүмкіндікетрі тең: Р(υ_2/ u₁) = Р(υ_1/ u₂) = Р, ал қатенің толық мүмкіндігі

(3.6)

Осыдан мынандай байланыс шығады:

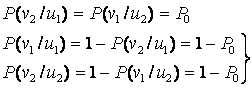. (3.7)

Оларды (3.4)-ке қойған соң мынаны аламыз:

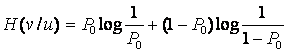. (3.8)

(3.3.) – тің толық өткізгіштік мүмкіндігін анықтау үшін J(u,v)=H(v)-H(v/u) – ді максимилдау керек. Берілген қатенің мүмкіндігі (4.8) –тың артынша, H(v/u) тұрақты, ал максимумды H(v) өзгертумен табу керек. Сигналдың энтропиясы H(v), (3.2) формуламен берілген, максималды мәні H₀(v)=1 –ні әртүрлі мүмкіндікті сигналдар кезінде, P(v₁)= P(v₂)=0.5 болғанда. (3.7) және (3.8) формулаларын (3.2) формуласына қойғанда екілік симметриялық арнаның өткізгіштік қабілетін аламыз:

. (3.9)

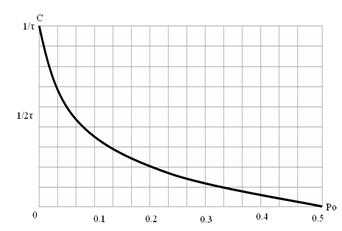
3.1 Сурет - Екілік арнаның өткізгіштілік қабілетінің қателік мүмкіндігіне р0 қатынасы

3.1 - суретінде С-ның екілік арнаның қателік мүмкіндігімен (3.9) қатынасы келтірілген. Р₀ өсуі өткізгіштік қабілеттің төмендеуіне алып келеді, содан ол Р₀ =0,5 кезінде нөлге тің болады. Бұл жағдайда (3.7)-ге сәйкес берілген және қабылданған сигналдар арасында қандай да бір байланыстар жойылады: Р(v₁/u₁)= Р(v₂/u₁)=1/2 и Р(v₁/u₂)= Р(v₂/u₂)=1/2. Р₀=1/2 – дың мәнісі бинарлы арнаға шекті болады.

4 Дәріс. Бөгеулері бар дискретті арна (жалғасы)

Мазмұны:

а) кедергісі және өткізгіштік қабілеті бар арнаға арналған теорема;

б) бөгеулі дискретті арналарының математикалық моделі;

в) ақпаратты үздіксіз түрде ұсыну;

г) сигналды қалпына келтіру сапасының критерилері.

4.1 Кедергісі және өткізгіштік қабілеті бар арнаға арналған теорема

.

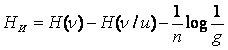Ақпаратты жіберу жылдамдығы:

, мұндағы 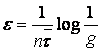. (4.1)

Арна бойынша ақпаратты жеткізудегі максималды жылдамдығы maxR=C

. (4.2)

Бір мезетте құру мүмкіндігі декодтық қателіктің аз ықтималдығында Р_ОД және ε аз өлшемдегі пайдасы Шеннон теоремасының шындығын дәлелдейді.

Жоғары мөлшердегі кедергісі бар дискретті арналарда ақпаратты жіберу теориясындағы негізгі мәндері бар теореманы Шеннон дәлелдеді. Бұл теорема келесі жолдармен қалыптасуы мүмкін.

Егер таратқыштың өнімділігі R_и C-ε, бұл жерде ε-өте аз шамада болғандықтан, барлық мәліметтерді аз мөлшердегі қателіктермен кодтау әдісі бар. Егер Rи>C болса, бұлай жіберу мүмкін емес. Әрбір топқа типтік ауысу мөлшері:

М_Г=2^nH(v/u) . (4.3)

Жалпы жағдайда ауысулар айқастандырылады, яғни бір ғана тізбек V_j .

Бірнеше тізбектің U бір тізбегі жіберілу нәтижесінде пайда болуы мүмкін.

Декодтаудағы қателік ықтималдығы:

. (4.4)

М_И – ақпаратты тасымалдауға арналған тізбек саны;

Р_пер – тасымалдаулардың айқастану ықтималдығы.

Бұл ықтималдық шамасы өте жақын болып табылады, бірақ Р_ОД пен М_И арасындағы тәуелділікті сипаттауға дұрыс бағыт береді.

Егер таратушынын энтропиясы Н_И тең болса, онда:

. (4.5)

.

Ақпаратты жіберу жылдамдығы:

где . (4.6)

Арна бойынша ақпаратты жеткізудегі максималды жылдамдығы maxR=C және

. (4.7)

Бір мезетте құру мүмкіндігі декодтық қателіктің аз ықтималдығында Р_ОД және ε аз өлшемдегі пайдасы Шеннон теоремасының шындығын дәлелдейді.

Жоғары мөлшердегі хабарларды дұрыс жіберу үшін жеткіліксіздік кодын қолдану керек. Егер R=C , онда ортақ келісілген ақпарат . Олай болса жеткіліксіздік коэффициенті:

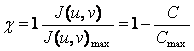. (4.8)

Баскаша айтқанда, теорема мәліметтерді аз ықтималдықтағы қателіктермен декодтауды P_ОД жіберу үшін, χ-ке тең болатын минималды жеткіліксіздік кодтары табылатыны аныктайды. Жіберу кезінде бинарлы сигналдардың минималды жеткіліксіздігі:

. (4.9)