- •Коммерциялық емес акционерлік қоғам
- •Ақпараттар теориясы
- •5В070400 – «Есептеу техникасы және бағдарламамен қамтамасыз ету» мамандығының барлық оқу бөлімінің студенттері үшін дәрістер жинағы
- •1 Дәріс. Сигнал, ақпарат және хабар
- •1.1 Хабар кездейсоқ үрдіс ретінде
- •1.2 Детерминделген сигналдарды бейнелеу формалары
- •1.1 Сурет - Сигналдардың бейнелеу формулалары
- •1.3 Хартли өлшемі. Ақпараттың сандық бағасы
- •1.4 Шеннон энтропиясы мен Больцман энтропиясының арасындағы байланыс
- •1.2 Сурет - Ықтималдылықты жағдайлардың айырмашылығы
- •1.4 Ақпарат түсінігі
- •2 Дәріс. Бөгеусіз дискретті арна
- •2.1 Ақпарат таратудың бөгеусіз дискретті арнасы
- •2.2 Арнаның өткізу қабілеті
- •2.3 Бөгеусіз арнаның өткізу қабілеті үшін теорема
- •2.4 Бөгеусіз дискретті арнаның математикалық моделі
- •2.1 Сурет - Екілік симметриялық арнадағы өту ықтималдығы
- •3 Дәріс. Бөгеулері бар дискретті арна
- •3.1 Бөгеу туралы ұғым
- •3.2 Бөгеулердің түрлері
- •3.3 Бөгеулі ақпаратты таратушы дискретті арна
- •3.1 Сурет - Екілік арнаның өткізгіштілік қабілетінің қателік мүмкіндігіне р0 қатынасы
- •4 Дәріс. Бөгеулері бар дискретті арна (жалғасы)
- •4.1 Кедергісі және өткізгіштік қабілеті бар арнаға арналған теорема
- •4.2 Бөгеулі дискреттік арналардының математикалық моделі
- •4.3 Ақпаратты үздіксіз түрде ұсыну
- •4.1 Сурет - Сигналдың түрлері
- •4.4 Сигналды қалпына келтіру сапасының критерилері
- •5 Дәріс. Үздіксіз арна
- •5.1 Үздіксіз сигналды ортогональды қатарларға жіктеу
- •5.2 Фурье қатарлары және олардың байланыс техникасында қолданылуы
- •5.3 Котельников теоремасы (Шеннонның негізгі теоремасы)
- •5.4 Үздіксіз арнаның өткізу қабілеті (бөгеусіз және бөгеулермен)
- •5.1 Сурет - үб арнасының үлгісі
- •6 Дәріс. Байланыс жүйесіндегі сигналдарды түрлендіру және қалыптастыру әдістері
- •6.1 Ақпарат тасушының модуляциялау әдістері
- •6.2 Гармоникалық модуляциялық сигналы
- •6.1 Сурет - Модулятор
- •6.3 Амплитудалық (ам), жиіліктік (чм), фазалық (фм) модуляция
- •6.2 Сурет - Амплитудалық – модуляцияланған сигнал
- •6.3 Сурет – Жм сигналының лездік жиілігі
- •7 Дәріс. Фазалық модуляция
- •7.1 Фазалық модуляция
- •7.2 Сигналдардың уақыттық, спектрлік және векторлық көріністері
- •7.4 Жиілік жолығының ұзындығы және жм және фм сигналдарының спектрлерінің айырмашылығы.
- •7.6 Сурет - Бессель функцияларының графиктері
- •8 Дәріс. Импульсті модуляция
- •8.1 Сурет – Әр түрлі импульсті модуляция сигналдары
- •8.2 Дискреттік модуляциялау әдістері
- •8.2 Сурет - Дискреттік модуляция кезіндегі сигналдардың уақыттық диаграммалары
- •8.3. Импульстер жүйесінің спектрі
- •8.3 Сурет - Импульстер жүйесінің спектрі
- •9 Дәріс. Бөгеуге тұрақты кодтау теориясы
- •9.1 Өткізгіштік қабілеті және құжаттарды жіберу жылдамдығы
- •9.2 Мәліметтердің артықшылығы
- •9.3 Тиімді кодтау теоремасы
- •10 Дәріс. Бөгеуге тұрақты түзетуші кодтар
- •10.1 Жалпы мәліметтер
- •10.2 Қателерді табудың және түзетудің негізгі принциптері
- •10.3 Кодалық қашықтық және кодтың түзету қабілеті
- •10.4 Кодтарды түзету классификациясы
- •11 Дәріс. Бөгеуге тұрақты түзетуші кодтар (жалғасы)
- •11.2 Үйірткі кодтар
- •12 Дәріс. Жүйелердің бөгеулерге тұрақтылық теориясы
- •12.1 Хабарлардың оптималды қабылдау шарттары
- •12.2 Оптималды қабылдағыштардың алгоритмдер мен сұлбаларын синтездеу, коррелияцилық қабылдағыш, үйлестірілген сүзгісі бар қабылдағыш
- •12.1 Сурет - Котельниковтың қолайлы қабылдағышы
- •13 Дәріс. Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Сурет - Котельников үйлесімді сүзгілі оптималды қабылдағышы
- •13.2 Модуляция түрлері және сигналды қабылдаудың әртүрлі
- •13.2 Сурет – ам, жм, фм сигналдарының эквивалентті энергияларын анықтау үшін
- •13.2 Салыстырмалы фазо-манипуляцияланған сигналдар
- •14 Дәріс. Көпарналы байланыс
- •14.1 Көпарналы байланыс
- •14.1 Сурет- Көпарналы байланыс арнасынын функционалды сұлбасы
- •14.2 Сигналдардың фазалық, жиіліктік, уақыттық бөлінуінің әдістері
- •14.2 Сурет - Арналардың уақытша бөлінуі
- •14.3 Сурет - цат-тің құрылымдық сұлбасы
- •15 Дәріс. Модуляцияның цифрлық әдістері
- •15.1 Ақпаратты қалпына келтіру және дискритизацияның принципі
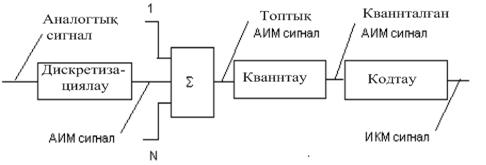
- •15.1 Сурет - Аналогтық сигналдың цифрлық икм сигналға айналу құрылымы
- •15.2 Импулсті - кодалық модуляция (икм)
- •Мазмұны
14.3 Сурет - цат-тің құрылымдық сұлбасы
АЦТ–тің құрылымы ЦАТ-тің құрамында болады. АЦТ - тің мұндай құрылымы 14.4 суретте көрсетілген. Аналогты сигнал таңдаулар және сақтаушылар құрылғының (ТСҚ) кірісіне келеді, онда дискреттеуге ұшырайды, яғни АИМ сигналына айналады. Бұл сигнал салыстыру құрылғысының (СҚ) кірісіне беріледі, ал ол өз кірісіндегі аналогтық сигналдардың мәндерін салыстыру үшін арналған компаратор болып табылады. Егер салыстыру құрылғысының бірінші кірісінде сигналдың мәні екіншісінен қарағанда үлкен болса, онда салыстыру құрылғысының кірісінде логикалық «1» сигналы орналасады, қарама қарсы жағдайда логикалық «0». Салыстыру құрылғысының екінші кірісіне ЦАТ-тің аналогтық шығысы қосылады.
ЦАТ-тің цифрлық кірістері басқару құрылғысының (БҚ) қорытындылау портына қосылған, мысалы микропроцессорға. БҚ ның кіріс портына СҚ ның цифрлық шығыстары қосылады. Кванттау процесі дәреже бойынша келесі түрде ағады. СҚ ның кірісінде таңдау және сақтау құрылғының (ТСҚ) шығысындағы сигналдың санауы (отсчеті) ең төменгі кірісіне беріледі. Алдымен үлкен разрядтардағы кодалық сөздің мәні анықталады. Одан кейін кіші разрядтар анықталып болған соң, келесі санаудың өңделуіне құрылғы дайын болады. Құрылғының жұмыс істеу жылдамдығы, яғни дискреттеу жиілігі, БҚ-ның жұмыс істеу жылдамдығымен ЦАТ-тің өзгерту жылдамдығына тәуелді.

14.4 сурет - АЦТ-тің құрылымдық сұлбасы
15 Дәріс. Модуляцияның цифрлық әдістері
Дәрістің мақсаты: модуляцияның цифрлық әдістермен танысу.
Мазмұны:
а) ақпаратты қалпына келтіру және дискритизацияның принципі;
б) импульстік -кодалық модуляция (ИКМ)-модуляция, дифференциялдық ИКМ;
в) ИКМ-30 кадрының құрылымы.
15.1 Ақпаратты қалпына келтіру және дискритизацияның принципі
Дискретизациядағы үздіксіз хабарламаларын қалпына келтіру. Дискретизация уақыт бойынша және деңгей арқылы орындалады.
Дискретизация уақыт бойынша орындалатын функция u(t) уақыт бойынша дискретті моменттің анықталуы tk.. Қортындысы үздіксіз функция u(t) барлығы едәуір көп мәндерде ауыстырылды uk={u(tk)Әдетте,есеп беру кезінде уақыт бойынша осьті тепе теңдік күйде алынады,яғни tk =k∆t. Интервал ∆t таңдауы Котельников теоремасы негінде жүзеге асады, шектелген спектірлік функция бойынша өзінің барлық мәндері анықталады, санаулы интервал арқылы ∆t=1/2F, мұнда F –спектр ені. Барлық импульстік модуляция түрлері дискретизация уақыт бойынша негізделеді.
Кейбір жағдайларда ешбір функциясыз хабарлама көрсетілу мүмкін, кейбіреулері ауыспалы. Мысалға мұндай сигналдың телевизорда бейнесін көрсетілуі, функция ретінде көрсетілуі мүмкін u(x,y,t) екі жақтағы кордината х және у және уақыт t, мұнда u -бейненің жарықтығы.
Деңгейлер
шкаласы бойынша дискретті шамалар жиі
бір қалыпты таңдалады:
![]() .
U функциясының айқын шамалары uk
шамаларымен
жуық шамаланатындықтан кванттау кезінде
қателік жіберіледі. Бұл
.
U функциясының айқын шамалары uk
шамаларымен
жуық шамаланатындықтан кванттау кезінде
қателік жіберіледі. Бұл
![]() қателігінің
шамасы ∆u
кванттауының
жарты қадамынан аспайды және рұқсат
етілетін шамаға дейін келтіріледі.
қателігінің
шамасы ∆u
кванттауының
жарты қадамынан аспайды және рұқсат
етілетін шамаға дейін келтіріледі.
![]() қателігі
кездейсоқ функция болып табылады және
шығыста жіберілетін хабарламаға қосымша
шу ретінде пайда болады.
қателігі
кездейсоқ функция болып табылады және
шығыста жіберілетін хабарламаға қосымша
шу ретінде пайда болады.
Дискретизация бір мезетте деңгей және уақыт бойынша кейін дискреттік техника әдістерімен кодталатын және жіберілетін үзіліссіз хабарламаларды дискреттікке түрлендіруге мүмкіндік береді. Кедергіге тұрақтылықты жоғарылату үшін кодтауды қолдану мүмкіндігі, сигналдарды өңдеудегі қолайлылық және байланыс құрылғыларының цифрлық есептеу машиналарымен байланысы байланыс жүйелерінің дискретизациясының артықшылықтары болып табылады.
Таңдаулар арқылы сигналдың жаңғыртуын ортогнальды және апроксимацияланатын полином типі мен жақындасу принципін: интерполяциянды, экстраполяциянды, үйлесімді анықтайтын ортогональды емес базистік функциялар негізінде жүзеге асыруға болады.
Сигналдың ортогональды емес көрсетілімдері үшін
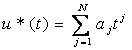 ,
(15.1)
,
(15.1)
немесе
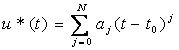 (15.2)
(15.2)
түріндегі дәрежелік алгебралық полиномдар қолданылады.
мұнда aj –нақты коэфициенттер.
Егер сигналдардың координаталары таңдамалардың айырымы түрінде берілсе, онда оны қалыпқа келтіргенде, ең алдымен, таңдамалардың тізбегінің санауы болады, кейін солар бойынша апроксимацияланатын u*(t) полиномын құрады. u*(t) апроксимацияланатын полиномының құрамында базистік функциялардың жүйесінің таңдауы дискретизацияның аппараттық құралдарының техникалық жүзеге асуының оңайлылығын қамтамасыз ететін қажеттіліктермен және сигналдың қалыпқа келуімен анықталады. Егер базистік функцияларды таңдау апроксимацияланатын полиномның мәндері таңдамалардың мәндерімен оларды санау кезінде сәйкес келетіндей боп таңдалса, мұндай полином интерполяциянды деп аталады.