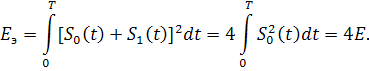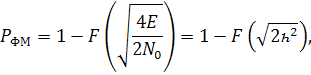13.1 Сурет - Котельников үйлесімді сүзгілі оптималды қабылдағышы

Осыған қарай үйлесімді сүзгі базасында оптималды қабылдағыш (13.1 суретті қара) көрсетілгендей құрылады.

Активті сүзгіге қарағанда үйлесімді немесе пассивті сүзгінің айырмышылығы, қабылдағыштағы үш бірдей элементің (тіректік тербеліс генераторы, көбейткіш және интегратор) орнын басады. Сұлба оңайлағандай көрінгенмен, үйлесімді сүзгіде оптималды қабылдағыштарды іске асыру кезіндегі туындайтын қиындықтар бар. Қиындық тудыратыны, сүзгі шығысындағы санақ корреляциялы когерентті қабылдағыштағыдай тура бастапқы фазасына дейінгідей шығарылуы керек. Бірақ, жіберілетін дәлдік өлшемі активті сүзгі шығысындағыдан кіші болуы керек. Активті сүзгіште қателік дыбысты жіберу ұзақтығымен салыстырғанда аз болуы жеткілікті, ал үйлесімді сүзгілеу кезінде оптималды қабылдағыш кірісіне келіп түсетін жоғары жиілікті радиоимпульстерін толықтыру периодтан аз болуы қажет. Бұл кемшіліктерді активті сүзгідегі когерентті тіректік тербелістерді іске асыру барысындағы қиындықтармен салыстыруға болады.

13.2 Модуляция түрлері және сигналды қабылдаудың әртүрлі

әдістері арқылы байланыс жүйесінің бөгеуілге тұрақтылығын талдау

Жоғарыда алынған байланыстарды қателіктің болу ықтималдығымен әртүрлі манипуляция түрлері бар екілік сигналдарға жіктейміз. Көп қолданылатын амплитудалы, жиілікті, фазалы және салыстырмалы фазалы манипуляцияланған сигналдарды қарастырамыз және олардың бөгеуге тұрақтылығын тексереміз.

а) амплитудалы манипуляцияланған сигналдар

Бұл жағдайда екілік сигналдардың бірі мысалы S\(f - 0 берілген. Осыған ұқсас сигналдар жүйесін пассивті кідірісті жүйе деп атау керек. Сонда қабылданатын сигналдар келесі түрде жазылады:

(13.3)

Б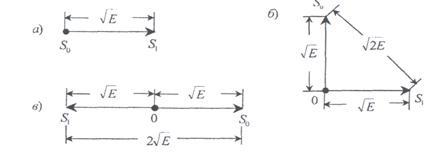 ұл жерде U_c -амплитуда, ω-жиілік, φ –бастапқы фаза. Екілік кеңістікте АМ сигналдары вектор түрінде (13.2, а сурет) көрсетілген.

13.2 Сурет – ам, жм, фм сигналдарының эквивалентті энергияларын анықтау үшін

АМ сигналдың эквивалентті энергиясының өлшемі:

(13.4)

Демек, қателік ықтималдығы келесі қатынаспен анықталады:

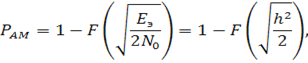(13.5)

h² = e/n₀ қабылдағыш кірісіндегі сигнал энергиясының ақ шу қуатының спектральді тығыздығына қатынасы.

Фазоманипуляциаланған сигналдар. ЖМ сигналдары сияқты фазоманипуляциаланған сигналдар белсенді кідірісі бар сигналдар жүйесі болып табылады. Себебі, әрбір өткізімге «0» немесе «1» деген екілік ақпараттық символдар сәйкес келеді. Кейбір жағдайда ФМ сигнал тасушы тербелістің фазасысың 180° ауытқуынан пайда болады. Нәтижесінде пайда болған сигнал ақпараттық гармоникалық тарату тербелісіне көбейтілген екі полярлық сигнал болып табылады.

Осылайша, ФМ сигнал мынадай түрде болады:

(13.6)

мұнда S0(t) =-S0(t) бір-біріне қарама-қарсы екені көрінеді. Олардың векторлық көрінісі (13.2 в) суретте көрсетілген.

Суретте көрсетілгендей, фазо-манипуляцияланған сигналдың векторлық кеңістігіндегі векторлардың ара қашықтығы басқа сигналдарға қарағанда ең жоғары. Осыған байланысты бұл сигналдар өзгеше және бөгеуілге тұрақты болады.

ФМ сигналдың эквиваленттік энергиясын мына формуламен анықтауға болады:

(13.7)

Қателік ықтималдығы мынаған тең:

	(13.8)

Егер ФМ, АМ және ЖМ сигналдардың қателік ықтималдығын салыстыратын болсақ, онда ФМ сигналы бастапқы екеуінің арасынан орын алады. Сондықтан ФМ (қарама-қарсы) ЖМ-ге (ортогоналды) ауысу кезінде энергия екі есе өсіп, эквивалентті 3 дБ-ге тең болады. Ал ЖМ мен АМ сигналдардың салыстырылуы нәтижесінде, ЖМ сигналдарын қабылдауды қолданғанда энергия екі есе аз кетеді.

Бірақ ФМ сигналдары ең бөгеуілге тұрақты болғанымен, оның когорентті қабылдауын ұйымдастыру күрделі қиындықтарға кездеседі. Қиындық техникалық тіректі (эталонды) синфазалы қабылдау сигналы қалыптасу кезінде болады.

Барлығымызға белгілі ФМ сигналының спектірінде тасушы тербелістің жиілігі болмайды. Сондықтан қабылданған сигналды баптауға тіректі тербеліс генераторын қолдануға болмайды. Тасушы сигналды қалпына келтіру үшін одақтық ғалымдар А.А. Пистолькорс (1933), В.И. Сифоров (1935), американ ғалымы Д. Костас ұсынған сызықсыз түрлендіргіш қолдану әдістерін пайдалануға болады.

Пистолькорстің оңай әдісін қарастырайық. Бастапқы кезеңде қабылдау тербелісінің жиілігі үлкейеді, сондықтан бұл манипуляцияның жайылуына әкеледі. Осыдан, So(t)=Uc cos (ω ct+ φ) тарату кезінде Uc cos2 (ωct+ φ)тербелісін аламыз, ал S(t) = Uc cos (ωсt+ φ + π) тарату кезінде, Uc cos2 (φct+ φ + π) = Uc cos 2(ωсt+ φ) тербелісін аламыз.

Фильтрациядан кейін, тіректі генератордың баптауларын өзгертуге жиілікті екіге бөлгенде пайда болған жиілікті тербеліс және оның аз деңгейлі бөгеуілі қолданылады. Бірақ, бөлгенде фазаның бірмәнділік болмаған үшін принципиалды қиындық туындайды. Тең кездейсоқтықпен фаза 0° және 180° мәндерін қабылдау мүмкін. Осыдан «0» символы «1» немесе кері мәнге айналады. Бұл эффект жойылуы мүмкін емес, себебі фазалық секіріс бөгеуілдің байланыс арнасына әсері кездейсоқ. Бұл кемшілік жоғарыда көрсетілген барлық әдістерге сәйкес. Сондықтан классикалық түрде ФМ сигналдар қолданылмайды.