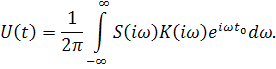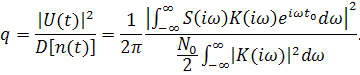- •Коммерциялық емес акционерлік қоғам
- •Ақпараттар теориясы
- •5В070400 – «Есептеу техникасы және бағдарламамен қамтамасыз ету» мамандығының барлық оқу бөлімінің студенттері үшін дәрістер жинағы
- •1 Дәріс. Сигнал, ақпарат және хабар
- •1.1 Хабар кездейсоқ үрдіс ретінде
- •1.2 Детерминделген сигналдарды бейнелеу формалары
- •1.1 Сурет - Сигналдардың бейнелеу формулалары
- •1.3 Хартли өлшемі. Ақпараттың сандық бағасы
- •1.4 Шеннон энтропиясы мен Больцман энтропиясының арасындағы байланыс
- •1.2 Сурет - Ықтималдылықты жағдайлардың айырмашылығы
- •1.4 Ақпарат түсінігі
- •2 Дәріс. Бөгеусіз дискретті арна
- •2.1 Ақпарат таратудың бөгеусіз дискретті арнасы
- •2.2 Арнаның өткізу қабілеті
- •2.3 Бөгеусіз арнаның өткізу қабілеті үшін теорема
- •2.4 Бөгеусіз дискретті арнаның математикалық моделі
- •2.1 Сурет - Екілік симметриялық арнадағы өту ықтималдығы
- •3 Дәріс. Бөгеулері бар дискретті арна
- •3.1 Бөгеу туралы ұғым
- •3.2 Бөгеулердің түрлері
- •3.3 Бөгеулі ақпаратты таратушы дискретті арна
- •3.1 Сурет - Екілік арнаның өткізгіштілік қабілетінің қателік мүмкіндігіне р0 қатынасы
- •4 Дәріс. Бөгеулері бар дискретті арна (жалғасы)
- •4.1 Кедергісі және өткізгіштік қабілеті бар арнаға арналған теорема
- •4.2 Бөгеулі дискреттік арналардының математикалық моделі
- •4.3 Ақпаратты үздіксіз түрде ұсыну
- •4.1 Сурет - Сигналдың түрлері
- •4.4 Сигналды қалпына келтіру сапасының критерилері
- •5 Дәріс. Үздіксіз арна
- •5.1 Үздіксіз сигналды ортогональды қатарларға жіктеу
- •5.2 Фурье қатарлары және олардың байланыс техникасында қолданылуы
- •5.3 Котельников теоремасы (Шеннонның негізгі теоремасы)
- •5.4 Үздіксіз арнаның өткізу қабілеті (бөгеусіз және бөгеулермен)
- •5.1 Сурет - үб арнасының үлгісі
- •6 Дәріс. Байланыс жүйесіндегі сигналдарды түрлендіру және қалыптастыру әдістері
- •6.1 Ақпарат тасушының модуляциялау әдістері
- •6.2 Гармоникалық модуляциялық сигналы
- •6.1 Сурет - Модулятор
- •6.3 Амплитудалық (ам), жиіліктік (чм), фазалық (фм) модуляция
- •6.2 Сурет - Амплитудалық – модуляцияланған сигнал
- •6.3 Сурет – Жм сигналының лездік жиілігі
- •7 Дәріс. Фазалық модуляция
- •7.1 Фазалық модуляция
- •7.2 Сигналдардың уақыттық, спектрлік және векторлық көріністері
- •7.4 Жиілік жолығының ұзындығы және жм және фм сигналдарының спектрлерінің айырмашылығы.
- •7.6 Сурет - Бессель функцияларының графиктері
- •8 Дәріс. Импульсті модуляция
- •8.1 Сурет – Әр түрлі импульсті модуляция сигналдары
- •8.2 Дискреттік модуляциялау әдістері
- •8.2 Сурет - Дискреттік модуляция кезіндегі сигналдардың уақыттық диаграммалары
- •8.3. Импульстер жүйесінің спектрі
- •8.3 Сурет - Импульстер жүйесінің спектрі
- •9 Дәріс. Бөгеуге тұрақты кодтау теориясы
- •9.1 Өткізгіштік қабілеті және құжаттарды жіберу жылдамдығы
- •9.2 Мәліметтердің артықшылығы
- •9.3 Тиімді кодтау теоремасы
- •10 Дәріс. Бөгеуге тұрақты түзетуші кодтар
- •10.1 Жалпы мәліметтер
- •10.2 Қателерді табудың және түзетудің негізгі принциптері
- •10.3 Кодалық қашықтық және кодтың түзету қабілеті
- •10.4 Кодтарды түзету классификациясы
- •11 Дәріс. Бөгеуге тұрақты түзетуші кодтар (жалғасы)
- •11.2 Үйірткі кодтар
- •12 Дәріс. Жүйелердің бөгеулерге тұрақтылық теориясы
- •12.1 Хабарлардың оптималды қабылдау шарттары
- •12.2 Оптималды қабылдағыштардың алгоритмдер мен сұлбаларын синтездеу, коррелияцилық қабылдағыш, үйлестірілген сүзгісі бар қабылдағыш
- •12.1 Сурет - Котельниковтың қолайлы қабылдағышы
- •13 Дәріс. Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Үйлесімді сүзгісі бар қабылдағыш
- •13.1 Сурет - Котельников үйлесімді сүзгілі оптималды қабылдағышы
- •13.2 Модуляция түрлері және сигналды қабылдаудың әртүрлі
- •13.2 Сурет – ам, жм, фм сигналдарының эквивалентті энергияларын анықтау үшін
- •13.2 Салыстырмалы фазо-манипуляцияланған сигналдар
- •14 Дәріс. Көпарналы байланыс
- •14.1 Көпарналы байланыс
- •14.1 Сурет- Көпарналы байланыс арнасынын функционалды сұлбасы
- •14.2 Сигналдардың фазалық, жиіліктік, уақыттық бөлінуінің әдістері
- •14.2 Сурет - Арналардың уақытша бөлінуі
- •14.3 Сурет - цат-тің құрылымдық сұлбасы
- •15 Дәріс. Модуляцияның цифрлық әдістері
- •15.1 Ақпаратты қалпына келтіру және дискритизацияның принципі
- •15.1 Сурет - Аналогтық сигналдың цифрлық икм сигналға айналу құрылымы
- •15.2 Импулсті - кодалық модуляция (икм)
- •Мазмұны
12.1 Сурет - Котельниковтың қолайлы қабылдағышы
Содан
соң, (СБ) салыстыру блогында апостериорлы
ықытималдылығы
![]() 12.4
теңсіздігіне сәйкес келетін Sj
,
сигналы жіберілгендігі туралы шешім
қабылданады.
12.4
теңсіздігіне сәйкес келетін Sj
,
сигналы жіберілгендігі туралы шешім
қабылданады.
Кіріс сигналын алдын-ала өлшеу арқылы интеграциялау операциясын сүзгілеу деп атайды. Осы қабылдағышқа сәйкес, үйлесімді жұмыс атқаратын екі блокты атауға болады: бірінші блок – осы жағдайда қолайлы болп табылатын сызықты сүзгі; екінші блок – сызықсыз шекаралық құрылғы (екі деңгейлік кванттағыш).
Үйлестірілген сүзгілері бар қабылдағыш. Бақыланып отырған кездейсоқ процеспен Z(t) мен Si(t) тірек сигналының скалярлы көбейтіндісін тек коррелятормен ғана емес, сонымен қоса тұрақты параметрлері бар пассивті сызықты сүзгі көмегімен де шешуге болады. Ондай сүзгілердің арасынан t=T, уақытында, яғни мәліметтерді алғанда шығысында сигнал/шум максималды болатын, беру функциясы K(iω) үйлестірілген сүзгілерді қарастырамыз. S(iω) – сүзгінің кірісіндегі сигналдың комплексті спектрі болсын, онда шығысында спектр S(iω)*K(iω) көбейтіндісмен табылады. Фурьенің кері түрлендіруін қолданып, t=t0 уақыт мезетіндегі шығыс сигналын жазамыз:
|
(12.5) |
Энергетикалық спектрі барлық G(ω) = No/2 жиіліктерінде бірқалыпты болатын n(t) ақ шуыл болсын. Фильтірдің шығысындағы шуыл:
|
(12.6) |
Виннер-Хинчин теоремасын қолдана отырып, сүзгінің шығысындағы бөгеу дисперсиясын жазамыз:
|
(12.7) |
Онда t=t0 уақыт мезетінде сигнал/шуыл қатынасы мына түрде жазылады:
|
(12.8) |
t=t0 уақыт мезетінде q шамасы максималды болғандағы K(iω) мәнін табу үшін Буняковский-Шварц теңсіздігін қолданамыз:
|
(12.9) |
мұндағы x(f),y(f) – кез-келген комплексті фунциялар. Теңдік жағдай тек x(f)-Cy(f), С = const болғанда ғана орындалады.
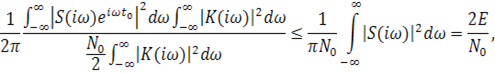 (12.10)
(12.10)
![]() (12.11
(12.11
Бұл қатынастан q максимум шамасы сигнал формасына тәуелді емес, толығымен сигнал энергиясының шуыл қуатының спектралды тығыздығына қатынасымен анықталады. Егер сүзгінің беру функциясы мынаған тең болса,
|
(12.12) |
онда q шамасы көбейеді. Мұндағы С – сүзгінің күшеюін көрсететін тұрақты, S(iω) сүзгінің кірісіне келіп түсетін функция.
Сүзгінің кіріс сигналының спектралды тығыздығы мен беру функциясын мына түрде жазамыз:
|
(12.13) |
|
(12.14) |
13 Дәріс. Үйлесімді сүзгісі бар қабылдағыш
Дәріс мақсаты: Үйлесімді сүзгісі бар қабылдағышпен танысу және модуляцияның әртүрлі түрі және сигналды қабылдаудың әртүрлі әдістері бар байланыс жүйесінің бөгеуілге тұрақтылығын талдау.
Мазмұны:
а) үйлесімді сүзгісі бар қабылдағыш;
б) модуляцияның әртүрлі түрі және сигналды қабылдаудың әртүрлі
әдістері бар байланыс жүйесінің бөгеуілге тұрақтылығын талдау;
в) ОФМ сигналдың когорентті қабылдауышы (полярлықтың теңеу
сұлбасы).
13.1 Үйлесімді сүзгісі бар қабылдағыш
Үйлесімді сүзгілердің негізгі қасиеттерін белгілейік:
1) Барлық мүмкін сызықты сүзгілердің ішінен үйлесімді сүзгі шығысында сигнал элементінің энергиясы мен шуыл қуатының спектральді тығыздығы қатынасының q =2E/N0 ең үлкен мәнін алуға мүмкіндік береді. Бұл мән сигнал пішініне тәуелді емес.
2) Үйлесімді сүзгі сигналдың түсу сәтіне байланысты инвариантты (инварианттылық–тәуелсіз), яғни кідіріс уақытына тәуелсіз. Басқа сөзбен айтқанда, сүзгі үшін оның кірісіне қашан сигнал келетіні маңызды емес. Кез келген жағдайда, егер ол пішіні бойынша үйлесімді болса, сүзгі шығысында сигнал/шуыл қатынасының максимумын аламыз. Ал коррелятор кідіріске инвариантты емес және сигналды максималдау үшін оның шығысында нақты тактілік синхронизация болуы қажет. Екі құрылғының да шығысындағы кернеу, тек сигналды жіберуді аяқтау сәтінде ғана сәйкес келетіндігін ескертеміз. Басқа сәттерде олар әртүрлі.
3) Үйлесімді сүзгі қабылданатын сигнал U(t) мен тірек сигналының S,(t), i =1,M арасындағы өзара корреляция функциясын анықтайтын құрылғы. Үйлесімді сүзгінің шығыс кернеуі U(to) басқа сызықты құрылғылардағыдай.
Бұл С тұрақты көбейткішті байланысты корреляция функциясы екені анық. (жоғарыда табылған скалярлы туындымен салыстырыныз).