11.2 Үйірткі кодтар

Екі тұтастай n және k сандарымен және жартылай номиналды немесе матрицалық генератормен сипатталатын сызықтық блоктың қодтың ерекшелігі мынау - кодтық сөздердің n-кортеждерінің әрбірі бір мәнді ретте кіріс хабарының k-кортeжімен анықталады. Тұтастай к саны мәліметтердің бит санын көрсетеді, олар блокты кодердің кірісін қалыптастырады. п тұтастай саны – бұл кодердің шығысындағы сәйкес келетін кодтық сөздегі разрядтардың жинақтық саны. Кодты (code rate) кодтаудың деңгейі деп аталатын k/n, қатынасы қосымша артықшылықтың шамасы болып табылады. Үйірткі код тұтас сандармен сипатталады n, k және К, мұндағы k/n қатынасы кодтау деңгейінің мәніне ие болады (кодталған битке өтетін ақпарат), блоктық кодқа арналған; дегенмен n блок ұзындығын немесе кодтық сөздің ұзындығын анықтамайды, яғни блоктық кодтардағыдай. К тұтас саны кодтық шектеудің ұзындығы (constrain! length); деп аталатын параметр болып табылады; ол жылжудың кодтайтын тіркемесінде к кортежінің разрядтар санын көрсетеді. Үйірткі кодтардың блоктық кодтардан маңызды ерекшелігі кодердің жадында n-кодтары болады, бұл кодтар үйірткі кодтау кезінде алынады, тек бір кіріс к кортежінің қызметі ғана болып табылмай, кіріс к кортеждерінің К алдыңғысының да ерекшелігі болып табылады. Практикада n және к - бұл кішігірім тұтас сандар, ал К кодтың қуаты мен күрделілігін бақылау мақсатында өзгереді.

Циклдік кодтар. Кез-келген (n,k) типті код матрица түрінде жазылады. к разрядты сызықты тәуелсіз жол бойымен және n символыменде де және керісінше.

Кодтардың барлық КК 1-КК-ні (туынды) циклдік жылжыту арқылы алынған кодтарды циклдік кодтар деп аталады.

Жылжу оңнан солға қарай жүзеге асады, сонымен қатар сол шеттегі соңғы символ КК соңына қарай ауысады.

Бастапқы 001011 – КК. КК матрицасы

.

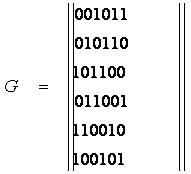Топты құрастыруда барлық КК саны топтық кодтағы КК мәнінен аз болып шығады. Қалай жалпы мәнді және КК-нің керекті мәнін қамтамасыз етуге болады? Сондықтан екілік барлық КК үшін коэфицент 0 немесе 1 бола алады.

Мысалы: 001011- екілік КК

Немесе .

х-тің ең үлкен дәрежесі нөлдік емес коэфицентпен көпмүшелік дәрежесі деп аталады.

Келесі циклдік көпмүшені “1” жылжытпай алуға болады, х пен бастапқы КК көбейту арқылы алуға болады:

Егер осы КК-ні (001011 және 010110) m2 бойынша жіктесек, онда нәтиже g(x) (х+1) көбейткенге тең болады:

001011

 => х +1 ,

010110

011101 

.

Матрицаны қатарын циклдік жылжыту үлкен разрядта сәйкес көпмүшені х-ке көбейтіп ,бір мезгілде көпмүшесінің нәтижесін есептегенге тең болады, яғни ( ) келтіруімен. болады

Бұл жағдайда кез-келген дұрыс КК, ЦК g(x)-ті басқа көпмүшеге көбейтудің нәтижесінде алуға m( ) болады, егер g(x) таңдаулы болса.

1) ЦК кез-келген дұрыс көпмүшесі (рұқсат етілген КК) g(x) көпмүшесіне қалдықсыз бөлінеді;

2) бұрыс КК g(x) көпмүшесіне қалдықсыз бөлінбейді, яғни кателік векторын анықтауға болады.

12 Дәріс. Жүйелердің бөгеулерге тұрақтылық теориясы

Дәріс мақсаты: Бөгеуге тұрақты түзеткіш кодтардың хабарларды

оңтайлы қабылдау критерийлерімен танысу, оптималды қабылдағыштың алгоритмдер мен сұлбаларың синтездеу, корреляциялық қабылдағыштың және үйлестірілген сүзгісі бар қабылдағыштың жұмысымен танысу.

Мазмұны:

а) хабарлардың оптималды қабылдау шарттары;

б) оптималды қабылдағыштың алгоритмдер мен сұлбаларын синтездеу, корреляциялық қабылдағыш, үйлестірілген сүзгісі бар қабылдағыш.