9.2 Мәліметтердің артықшылығы

Мәліметтер жинағы ретінде компьютерге орыс тілінде мәтін енгізетін операторды қарастырамыз. Әріптердің мәтінде әр түрлі ықтималдықпен пайда болатыны мәлім. Мысалы, А әрпі Ц немесе Ю әрпіне қарағанда анағұрлым көбірек беріледі. Бұдан басқада, келесі әріптің пайда болуы, алдындағы әріпке тәуелді. Дауысты дыбыстардан кейін Ь, Ъ және Ы әрпінің болмауы мәлім. Е әрпінің қатарынан үш рет болуы өте сирек болады («змееед» сөзінде). Жады жоқ таратушыға қарағанда, «жады бар» таратушы шығысында (тәуелді мәліметтер) мәліметтер дұрыс пайда болады, қателер азырақ болады. Осылай, біз мәліметтер артықшылығы деген түсінік кіргіземіз. Оны формалді түрде мына ара қатынас арқылы табуға болады:

. (9.3)

Яғни, энтропия неғұрлым көп болса, соғұрлым таратқыштың мәлімет шығаруы аз, ал керісінше артық мәліметтің шамасының көлемі 0≤ρ≤1 аралығында болады.

Берілген шама әріптер (символдар) n санын сипаттайды, олар таратқыштың берілген мәліметтер көлеміне байланысты. Артық шаманың көлемін былай табамыз:

. (9.4)

өлшемі қысу коэффициенті деп аталады. Ол мәліметтерді қандай көлемге дейін қысуға болатын шамасын көрсетеді, егер оның құрамындағы артық шаманы алып тастасақ та сондай мәнге ие боламыз. Мысалы, телеграмманы текст түрінде жіберген кезде олардың құрамындағы тыныс белгілерін оңай қалпына келтіруге болады.

Әріптер мен сөздердің арасында байланыс болса, онда оларды қайтадан қалпына келтіру мүмкіндігі бар.

Артық мән параметрінен басқа тағы да басты характері жылдамдықпен сипатталуы мумкін симв/с хабар тарату оның шығарушылығымен сипатталады, ол энтропияны уақыт бірлігімен сипаттайды.

. (9.5)

Егер энтропия максималды болса ол log N тең, ал өлшемі , бит/с, ақпарат таратушының жылдамдығы деп аталады.

Таратушының мәні – ақпараттың бір секунд ішіндегі үздіксіз жұмысының орташа мәні.

9.3 Тиімді кодтау теоремасы

Тиімді кодтаудың теоретикалық негізі К.Шеннон теоремасымен анықталады. Бұл теореманың мәні мынада: таратқышта Н (бит символға) энтропиясы бар болсын, ал арнада өткізу қабілеттілігі С (бит секундына) тең. Сондықтан хабарды таратқыш шығысында былай кодтауға болады, Е-қаншалықты аз болсада орташа жылдамдықпен C/H-E секундына арна арқылы бір символ жібере аламыз. Хабар элементтерінің орташа жылдамдығынан артық, C/H жылдамдығымен ақпараттар жіберу мүмкін емес.

Айта кету керек, ДХ бөгеуілсіз байланыс арнасы арқылы жібергенде, 2 шарт орындалуы керек.

1 шарт: кодтық комбинациялар әр түрлі болуы керек. Яғни қабылдағышта декодтау керек және керекті ДХ элементтерімен байланыста болуы керек.

2 шарт: кодтау тәсілі максималды пайдалы болу керек, жіберілген хабар қысқа немесе оның жіберу жылдамдығы максималды болуы керек.

1 шартты қанағаттандыртатын тиімді кодтарды префиксный деп атайды.

Себебі, бұл кодтарда алдыңғы комбинация ешқандай бөліктен немесе префикс басқа комбинацияларда бола алмайды.

2 шартты қанағаттандыратын кодтар оптималды деп есептеледі.

Хабардың таратқышында кодтың минимал оптималды орташа мәні n_min , бір-біріне тәуелсіз мына теңдікте жатады.

. (9.6)

Оптималды екілік код үшін (в=2, m=2).

Хабардың бір элементіне сай келетін нақты кодтың орташа мәні былай анықталады:

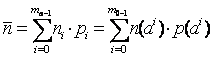. (9.7)

. (9.8)

(9.7) мәнді, (9.8) қойсақ, онда оптималдылық шарты n=n_min

. (9.9)

Сонымен, А хабарының aⁱ элементіне сәйкес келетін кодалық комбинациясының n_i дәрежесінің мәні оптималды тиімді кодта оның түсуінің p_i ықтималдығына тәуелді. Ықтималдылығы неғұрлым көп болса, соғұрлым кодтық комбинацияның дәрежесі аз болады және керісінше. Осыған байланысты, мұндай кодтауды статистикалық (ықтималдылықты) деп те атайды. Сонымен бірге, статистикалық (тиімді) кодтар біркелкі емес кодтауға жатады. Таратқыш кодерінің артықшылығын келесі формуламен есептейді:

. (9.10)

Артық шығыны нөлге жуық болатын, оптималдыға жақын екілік тиімді кодтың мысалы ретінде Шеннон-Фано мен Хаффменнің кодын айтуға болады.

Шеннон-Фаноның әдісімен екілік кодтаудың принципін қарастырайық. Екілік сивол элементтері ықтималдығының азаю ретімен бағанға (топ) ретінде орналасады. Кодтаудың бірінші бөлімінде бұл топ мүмкіндігінше ықтималдықтарының қосындысы бірдей болатын екі топқа бөлінеді. Бірінші топтың барлық элементтерін 0 символымен, ал екінші топтың І символымен белгілейді. Кодтаудың екінші бөлімінде ықтималдықтары бірдей әр топты тағыда екі топқа жіктейді. Бұл процесс бір элементтен тұратын топтар шыққанша жалғасады.

(9.1-кестеде) Шеннон-Фаноның тармақталған ықтималдықпен ДХ таратушыға тиімді кодты құрудың мысалы келтірілген:

, , , .

Берілгені: Н (А)=1,75 бит, H_max= 2 бит, r(A)=0.125.

Құрылған код үшін: бит, n_min=1.75 бит, Сәйкесінше, берілген код оптималды. 10.1 Кестеде берілген алғашқы код салыстыру үшін келтірілген: бит. / = к_сж қатынасы өрнегін қысу коэффициенті деп атайды. Мұндағы К_сж=1,15.

9.1 кесте - Шеннон-Фано тиімді кодын құрудың мысалы

А {ai}	{pi}	Кодтау жолдары			Тиімді код			Алғашқы код
		I	II	III	Код комб.	ni таңба	Код комб.		niпр таңба
а3 а1 а0 а2	0,5 0,25 0,125 0,125	0 1 1 1	- 0 1 1	- - 0 1	0 10 110 111	1 2 3 3	11 01 00 10		2 2 2 2