6.1 Сурет - Модулятор

Модуляцияланған сигналда (6.1) лездік бұрыштық жиілік толық фазаның уақыт бойынша туындысына тең

. (6.2)

(6.2) формуладан, толық фаза

. (6.3)

Модуляцияланған сигналдардың параметрлерін анықтау кезінде әдетте, модульдеуші сигналды u_m(t) нормаланған деп санайды, яғни максималды абсолютті лездік мән бірге тең - , ал орташа қуат , - сигнал амплитудасының коэффициенті.

Гармоникалық тасушы модуляциясының басты ерекшелігі – спектрдің тасушы жиілігінің маңындағы аймаққа көшіруі. Осы жағдай радиотехникада, көпканалды радиобайланыстарда тек модуляцияланған сигналдарды қолдануға әкелді.

6.3 Амплитудалық (ам), жиіліктік (чм), фазалық (фм) модуляция

6.3.1 Амплитудалық модуляция кезінде, тасушы сигналдың амплитудасы модуляциялайтын сигналдың u_m(t) лездік мәндеріне пропорционалды түрде өзгереді, яғни, өсімше алып келесіге тең болады:

. (6.4)

Бұндағы А₀ – тасушы амплитудасы; а - пропорционалдық коэффициент, ол А(t) амплитудасы әрқашан он мәнде болатындай етіп таңдалынады. АМ кезінде тасушының жиілігі мен фазасы өзгеріссіз қалады.

АМ сигналдың уақыттық диаграммасы 5.2 суретте көрсетілген, суреттен көрініп тұрғандай, u_m(t)-ның лездік мәндеріне сәйкес тасушы амплитудасы А_о өсімше алып A_{m max} мәніне дейін өседі, немесе өсімше алып A_min мәніне дейін азаяды. Назар аударатын сәт, А(t) амплитудасы модуляцияланған u_m(t) сигналының формасын қайталайды. АМ сигналында А(t) амплитудасы жоғары жиілікті толтырудың айналдырушысы болып табылады. (6.2,б - суретінде ол штрихталған сызықпен көрсетілген).

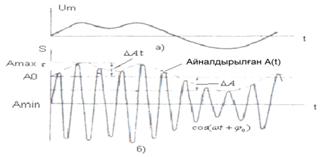
а) u_m (t) модуляциялайтын сигнал; б) АМ сигнал.

6.2 Сурет - Амплитудалық – модуляцияланған сигнал

Модуляция коэффициенті:

. (6.5)

Математикалық моделі:

. (6.6)

6.3.2 Жиілікті модуляция кезінде модуляцияланған сигналдың жиілігі ω_о-ден ауытқуы u_m(t) модульденген сигналдың лездік мәніне пропорционалды болады:

. (6.7)

мұнда, ∆ω_Д –пропорционалдылық коэффициенті

∆ω_Д девиация жиілігі деп аталады, және ол ω₀ жиілігінің үлкен ауытқуына тең болады. ЖМ сигналдың өзгеруі графикалық түрде 6.3 - суретте көрсетілген, мұнда ∆ω_Д жиілік девиациясы жиіліктің үлкен ауытқуына сәйкес келеді ∆ω_Д=∆ω_-, себебі ∆ω₊ <∆ω_. u_m(t)-ның өлшемі нормаланған, мұнда| u_m(t)|≤1.

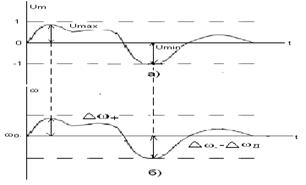
а) модульдеуші сигнал; б) лездік жиіліктің өзгеруі.

6.3 Сурет – Жм сигналының лездік жиілігі

Девиация жиілігі жиілікті модулятордың басты параметрлерінің бірі болып табылады және ол бірлік герцтен жүздік мегагерцке дейінгі мәндерді қабылдай алады. Бірақ, келесі шарт орындалуы керек << .

ЖМ сигналының толық фазасы (8.7) жиілігімен интегралдау әдісімен табамыз:

. (6.8)

Мұнда, ψ_о интегралдау тұрақтысы.

Яғни, ЖМ сигналының математикалық моделі былай жазылады:

. (6.9)

Бұл көрсеткішке U_m(t) интеграл белгісіне кіргендіктен, ЖМ-ны көбіне интегралды модуляция түрі деп атайды.

7 Дәріс. Фазалық модуляция

Дәрістің мақсаты:фазалық модуляция ақпаратымен және АМ, ЖМ сигналдарының уақыттық, спектрлік және векторлық көріністерімен танысу.

Мазмұны:

а) фазалық модуляция;

б) АМ және ЖМ сигналдарының уақыттық, спектрлік және векторлық

көріністері.

7.1 Фазалық модуляция

Фазалық модуляция кезінде, модуляцияланған сигнал фазасының ауытқуы сызықтыға қарағанда модуляцияланатын сигналдың Um (t) лездік мәніне пропорционалды өзгереді.

. (7.1)

-фаза девиациясы деп аталатын пропорционалды коэффициент. Бұл коэффициенттің физикалық мағынасы 7.1 - суретте көрсетілген, онда модуляцияланатын сигнал және ФМ сигналының толық фазасы суреттелген. Um (t) сигналының күшеюімен, толық фаза сызықты заңға қарағанда уақыт бойынша тезірек өседі. Сигналдың мәндерінде Um (t)<0 көтерілу жылдамдығы басылады. Um (t) экстремалды мәнге жеткенде, фазаның абсолютті көлемінің ауытқуы сызықтыға қарағанда көбірек болады. 7.1б суретінде, жоғары және төмен фазасының максималды ауытқуы көрсетілген. Фазаның сызықтыға қарағанда көбірек ауытқуы фазалық девиация . деп аталады. радианмен өлшенеді және бірліктен он мың радианға дейін мәндерді қабылдай алады.

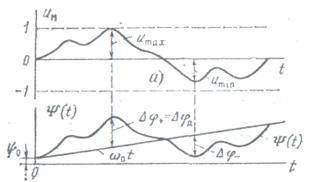
а) модуляциялайтын сигнал, б) толық фазаның өзгерісі

7.1 сурет - ФМ сигналдың толық фазасы

Математикалық моделі:

(7.2)