§1.2.2.4. Симплекс-метод

Симплекс-метод [98-99] является методом прямого поиска. Благодаря простоте и высокой эффективности при оптимизации сложных функций, этот метод получил широкое распространение [100]. Метод заключается в том, что движение к оптимальному значению аргументов функции осуществляется путем последовательных отражений некой фигуры, называемой симплексом. В m-мерном пространстве (целевая функция имеет m переменных) симплекс представляет собой фигуру с m+1 вершинами, не принадлежащую одновременно ни одному пространству меньшей размерности. Так, в одномерном случае симплекс является отрезком, в двумерном – треугольником, в трехмерном – тетраэдром. Чаще всего используются симплексы с равными расстояниями между вершинами. Измеряются значения целевой функции в вершинах симплекса. При поиске максимума движение происходит от вершины с наименьшим значением целевой функции к противоположной грани симплекса, который является зеркальным отражением предыдущего относительно грани, противоположной вершине с наименьшим значением целевой функции. Многократное отражение наихудших вершин приводит к шаговому движению центра симплекса к цели по некоторой ломаной линии (рис.1.16). За исключением начального момента, когда необходимо вычислить m+1 значение функции, на каждой итерации требуется всего одно ее вычисление.

Постоянный размер симплекса не обеспечивает одновременно и высокую скорость движения симплекса и точность отыскивания экстремума. Поэтому для быстрого и точного решения задачи требуется изменение размеров симплекса в процессе поиска. Этот метод предусматривает постепенное уменьшение

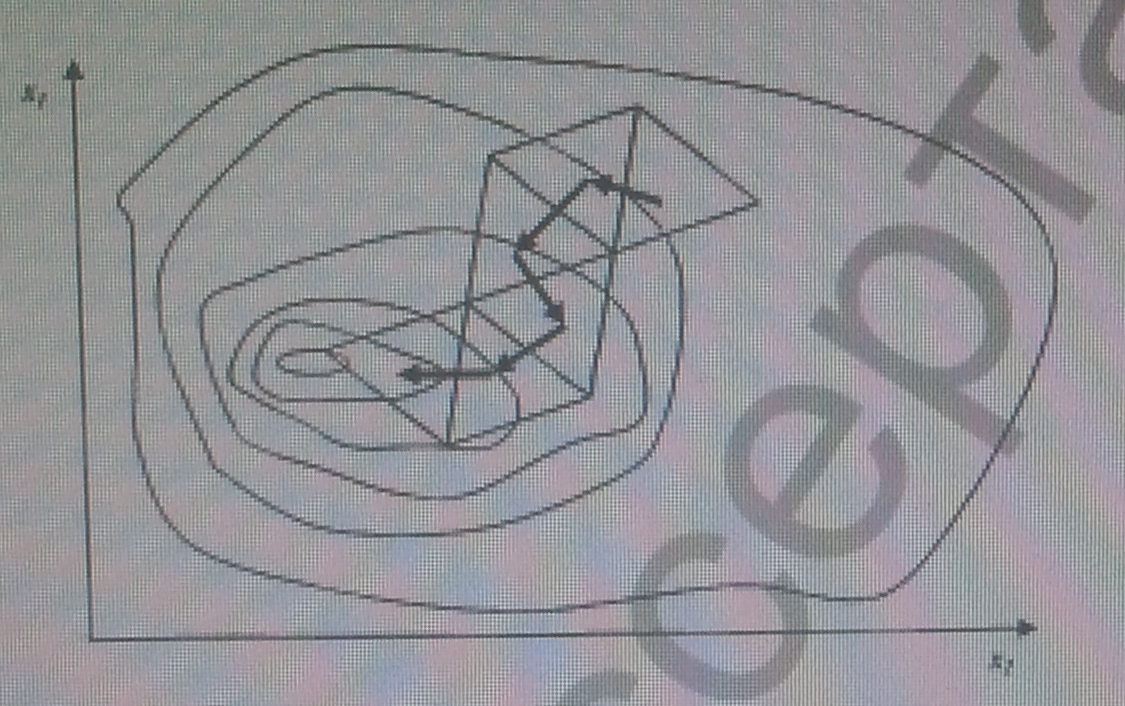
Рис.1.16. Характерное движение симплекса на плоскости двух переменных

расстояние между вершинами симплекса с сохранением одной вершины (последней найденной вершины или вершины с наилучшим значением оптимизируемой функции).

Симплекс-метод не уступает по эффективности градиентным методам, при этом существует возможность нахождения глобального экстремума оптимизируемой функции.

Кроме того, алгоритм не требует сложных вычислений, все операции формализованы, каждое измерение целевой функции позволяет двигаться к цели. Однако эффективность этого метода снижается при наличии помех. Для эффективной работы алгоритма необходимо, чтобы положение максимума целевой функции не менялось со временем и не зависело от предыстории, а целевая функция была стационарна во времени, что часто не выполняется в оптических системах, например, из-за гистерезиса адаптивного зеркала и изменения функций отклика адаптивного зеркала вследствие его нагрева или деполяризации.

§1.2.2.5. Генетический алгоритм

Часто оптимизируемая функция обладает большим количеством экстремумов. Это обстоятельство значительно затрудняет применение классических методов оптимизации. В связи с этим встает задача построения таких методов оптимизации, которые были бы способны отыскивать решения практически при полном отсутствии предложении о характере исследуемой функции. Одними из таких методов являются так называемые эволюционные методы поиска и, в частности, генетические алгоритмы, моделирующие процессы природной эволюции.

Генетические алгоритмы предназначены для решения задач оптимизации, например, нахождение максимального значения функции. В основе генетического алгоритма лежит метод случайного поиска. Основным недостатком случайного поиска является то, что часто необходимо значительное время для решения задачи. Для того, чтобы избежать таких расходов времени, применяются биологические методы, открытые при изучении эволюции и происхождение видов. Как известно, в процессе эволюции выживают наиболее приспособленные особи. Это приводит к тому, что приспособленность популяции возрастает, позволяя ей лучше выживать в изменяющихся условиях.

Впервые численный алгоритм, основанный на имитации развития популяции, был предложен в 1975 году Джоном Холландом (Jhon Holland) [102]. Он получил название «репродуктивный план Холланда» и лег в основу вариантов генетических алгоритмов.

Представление объектов

Из биологии известно, что любой организм может быть своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора [103]. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе. Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются числовые массивы. В задаче нахождения глобального экстремума какой-либо функции, этот числовой массив соответствует набору аргументов этой функции. Значение этой функции - есть числовое представление фенотипа. Таким образом, каждая особь со своим генотипом и фенотипом представляет собой возможное решение задачи оптимизации[104].

Для того чтобы определить фенотип объекта (то есть значения признаков, описывающих объект) нам необходимо только знать значение генов, то есть генотип объекта. Его также называют особью. Таким образом , в реализации генетического адгоритма хромосома( упорядоченная последовательность генов) представляет собой массив чисел генов фиксированной длины.

Основные генетические операторы

В теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание( его также называют кроссовер или кроссинговер) [105]. Этот оператор определяет передачу генов родителей потомкам. Действует он следующим образом: из популяции выбираются две особи, которые будут родителями; определяется(обычно случайным образом) точка разрыва; потомок определяется как конкатенация части первого и второго родителя. Рассмотрим пример: Хромосома_1: {0000000000}; Хромосома_2: {1111111111}; Допустим, разрыв происходит после 3-го гена хромосомы, тогда в результате получается две дочерние хромосомы : Хромосома_1: {0001111111}; Хромосома_2: {1110000000}; Затем с вероятностью 0,5 определяется одна из результирующих хромосом в качестве потомка.

Данный тип кроссовера называется одноточечным, т.к. при нем родительские хромосомы разрезаются только в одной случайной точке. Также существует 2-ч точечных кроссовер, в котором точек разрыва 2. Кроме описанных типов кроссовера есть еще однородный кроссовер. Его особенность заключается случайным образом из соответствующих генов родителей. Для этого вводится некоторая величина 0<p<1, и если случайное число больше

p, то на n-ю позицию хромосомы потомка попадает n-й ген первого родителя, в противном случае к потомку попадает ген второго родителя. Такая операция проводится для всех генов хромосом.

Следующий генетический оператор предназначен для того, чтобы поддерживать, разнообразие особей и популяции. Он также необходим для «выбивания» популяции из локального экстремума и способствует защите от преждевременной сходимости. Этот оператор называется оператором мутации[106]. При использовании данного оператора случайно выбранный ген, хромосом в определенной вероятностью меняется на случайно выбранное число.

Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосомы делятся на 2 части, и затем они меняются местами. Схематически это можно представить следующим образом: 01234567879>>6789012345.

Схема функционирования генетического алгоритма

В этом пункте представлена схема функционирования генетического алгоритма. Для оптимизации функции F, зависящая от нескольких аргументов в его классическом варианте.[104].

1) В начальный момент времени t=0 случайным образом сформировать начальную популяцию, состоящую из k особей : , где m-число аргументов оптимизируемой функции F.

2) Вычислить приспособленность каждой особи , i=1…k.

Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.

3) Выбрать две особи и из популяции

4) Произвести операцию кроссовера

5) С определенной вероятностью (вероятностью мутации P) выполнить оператор мутации

6) С определенной вероятностью (вероятностью инверсии P) выполнить оператор инверсии

7) Поместить полученную хромосому в новую популяцию.

8) Выполнить операции, начиная с пункта 3, k раз, заполнив новую популяцию

9) Увеличить номер текущего поколения t=t+1.

10) Если выполнилось условие остановки, то завершить работу, иначе переход на шаг 2.

Наибольшую роль в успешном функционировании алгоритма играет этап отбора родительских хромосом на шаге 3. При этом возможны различные варианты. Наиболее часто используется метод отбора, называемый рулеткой и пропорциональным отбором. При использовании такого метода вероятность выбора хромосомы определяется ее приспособленностью, то есть вероятностью передачи признаков более приспособленными особями потомкам возрастает.

Другой часто используемый метод – турнирный отбор . Он заключается в том, что случайно выбираются несколько особей из популяции (обычно 2), из которых родителем становится особь с наибольшей приспособленностью. Кроме того, в некоторых реализациях алгоритма применяется так называемая стратегия элитизма. Которая заключается в том , что особи с наибольшей приспособленностью гарантированно переходят в новую популяцию. Использование элитизма обычно позволяет ускорить сходимость генетического алгоритма. Недостаток использования стратегии элитизма в том, что повышенная вероятность попадания алгоритма в локальный минимум.

Модели генетических алгоритмов

В этом пункте приведено описание некоторых модификаций генетического алгоритма.

1) Канонический генетический период [102]. Данная модель алгоритма является классической, и ее характеристики:

• Фиксированный размер популяции

• Фиксированная разрядность генов

• Пропорциональный отбор

• Особи для скрещивания выбираются случайным образом

• Одноточечный кроссовер и одноточечная мутация

• Следующее поколения формируется из потомков текущего поколения без «элитизма». Потомки занимают места своих родителей.

2) Алгоритм с замещением наименее приспособленной особи [104]. В данном алгоритме используется специфичная стратегия отбора . Вначале как я в классическом случае, популяция инициализируется, причем получается только один потомок , который оценивается и занимает место наименее приспособленной особи. После этого снова случайным образом выбираются 2 особи, и их потомок занимает место особи с самой низкой приспособленностью. Таким образом, на каждом шаге популяции обновляется только одна особь. Отсутствует выделенные эпохи формирования новых поколений. Подводя итоги, можно выделить следующие характерные особенности:

• Фиксированный размер популяции

• Особи для скрещивания выбираются случайным образом

• Ограничений на тип кроссовера и мутации нет

• В результате скрещивания особей получается один потомок, который занимает место наименее приспособленной особи.

3) Гибридный алгоритм [107,108]. Использованные гибридного алгоритма позволяет объединять преимущества генетического с преимуществами классических методов. Генетические алгоритмы позволяют находить решение , близкое к оптимальному но точнее определение максимума функции зачастую занимает очень много времени в силу стохатичности принципов работы алгоритма. Поэтому возникла идея использовать генетический алгоритм на начальном этапе для эффективного поиска окрестности глобального экстремума, а затем, взяв лучшую особь, применить один из «классических» методов оптимизации. Характеристики алгоритма:

• Фиксированный размер популяции

• Любые комбинации стратегии отбора и формирования следующего поколения

• Ограничений на тип кроссовера и мутации нет

• Генетический алгоритм применяется на начальном этапе, а затем после небольшого числа итераций в работу включается метод поиска локального экстремума.

4) Островная модель генетического алгоритма [104]. Эта модификация также заимствована из биологии с следующей ситуации: имеется группа близкорасположенных островов, на которых живут популяции особей одного вида. Эти популяции развиваются независимо, и только изредка происходит обмен представителями между популяциями. Основная модель генетического алгоритма использует описанный принцип для поиска решения. Данная модель генетического алгоритма обладает следующими свойствами:

• Наличие нескольких популяции, как правило, одинакового фиксированного размера.

• Любые комбинации стратегий отбора и формирования следующего поколения в каждой популяции. Можно сделать так, что в разных популяциях будут использоваться разные комбинации стратегий.

• Ограничений на тип кроссовера и тип мутаций нет.

• Случайный обмен особями между «островами» после определенного шага схемы генетического алгоритма.

5) Алгоритм с периодическим перезапуском [109] . Данный алгоритм довольно быстро сходится из-за того, что в нем нет мутаций, используются популяций небольшого размера, и отбор особей в следующее поколение ведется и между родительскими особями и между потомками. Из-за этого после некоторого количества эпох алгоритм может сойтись к локальному экстремуму. После этого алгоритм перезапускается, причем лучшая особь копируется в новую популяцию, а оставшиеся особи подвергаются сильной мутации (мутирует примерно треть генов хромосомы) и поиск повторяется. Ещё одной специфической чертой является стратегия скрещивания: все особи разбиваются на пары, причем скрещиваются только те пары, в которых хромосомы особей существенно различны. При скрещивании используется так называемый – половинный однородный кроссовер – это разновидность кроссовера, в котором каждому потомку попадает ровно половина генов хромосомы от каждого родителя. Таким образом, модель обладает следующими свойствами:

• Фиксированный размер популяции.

• Перезапуск алгоритма после нахождения решения после определенного шага.

• Небольшая популяция.

• Особи для скрещивания разбиваются на пары и скрещиваются при условии существенных отличий.

• Отбор в следующее поколение проводится между родительскими особями и потомками.

• Используется половинный однородный кроссовер.

• Макромутация при перезапуске.

Какой из перечисленных алгоритмов наиболее эффективен, зависит от решаемой задачи и вида оптимизируемой функции.

Таким образом, генетические алгоритмы представляют мощный аппарат для решения задач оптимизации. Разработано большое количество различных модификаций и усовершенствований генетического алгоритма, которые повышают его эффективность и позволяют с той или иной степенью точности предсказать требуемое вычислительное время [106,110]. В последнее время генетический алгоритм нашёл широкое применение для решения различных прикладных задач лазерной физики [107-108,111-112].

Выводы:

Таким образом, подводя сравнение различных итерационных алгоритмов можно сделать следующие выводы:

1) алгоритм последовательного градиентного спуска для случая восстановления фазы по одному распределению интенсивности эквивалентен алгоритму минимизации ошибки, а в случае двух известных распределений интенсивности имеет сходство с алгоритмом Гершберга- Сакстона;

2) важным критерием при выборе того или иного метода является скорость его сходимости. В ходе исследований было установлено, что наиболее быстрой сходимостью из предложенных методов обладает INPUT-OUTPUT алгоритм.

3) вопрос получения однозначного решения для задачи восстановления фазы из распределений интенсивности так же представляет большой интерес. При решении двумерных задач данные методы позволяют получить однозначное распределение фазы.

4) алгоритмы глобального поиска имитирующие процессы эволюции в природе способны отыскать глобальный экстремум многоэкстремальной функции.