7. Сводные характеристики выборки результатов испытания хлопковых волокон, их распространение на генеральную совокупность - партию.

При исследовании свойств совокупность результатов отдельных измерений заменяют сводными характеристиками. К основным числовым характеристикам случайных величин относятся: среднее значение, дисперсия, среднее квадратическое отклонение, коэффициент вариации, размах варьирования.

Партией материала называется комплектуемая на производстве масса материала одного качества и происхождения и оформленная одним документом. Чтобы определить отдельные показатели качества партии материала или изделий, отбирают образцы. Часть образца – проба.

В математической статистике партию продукции рассматривают как генеральную совокупность единиц любой продукции, а ее исследуемую часть называют выборкой.

Чтобы выборка отражала свойство партии продукции и позволяла прогнозировать их, выборку необходимо отбирать по определенным правилам. Отклонение от них исключает возможность распространять выборочные оценки на всю партию материала.

Объем выборки определяется неравномерностью материала и величиной доверительных границ или интервала, в пределах которых должно находиться искомое значение показателя качества всей партии материала. Чем больше неравномерность материала и чем меньше задаваемая величина доверительного интервала, тем большим должен быть объем выборки, который по возможности принимают минимальным для ускорения испытаний.

Правила отбора единиц штучной продукции в выборку регламентируются в ГОСТ 18321-73. Ими следует руководствоваться и для любых текстильных материалов. При составлении выборок каждая единица из партии продукции должна иметь одинаковую вероятность (возможность) попасть в выборку; а для того, чтобы выборка была представительной, необходимо, чтобы она была составлена случайно.

Подготовка выборок к испытаниям.

С изменением влажности материала меняются его свойства (прочность, растяжимость, выносливость, электропроводность, масса и др.) Поэтому свойства волокон, нитей, полотен и изделий надо измерять и прогнозировать при постоянной нормальной влажности, которую они приобретают после выдерживания в течение определенного минимального времени при нормальных климатических условиях (относительная влажность воздуха , а температура воздуха t= 20±2˚C)

При исследовании свойств совокупность результатов отдельных измерений заменяют сводными характеристиками. К основным числовым характеристикам случайных величин относятся: среднее значение, дисперсия, среднее квадратическое отклонение, коэффициент вариации, размах варьирования.

Расчет сводных выборочных характеристик при малом числе испытаний n<50 производится по формулам:

Среднее значение выборки: где -отдельные результаты измерений; n-объем выборки;

Дисперсия (отклонение от среднего):

Среднее квадратическое отклонение различается на смещенное S и несмещенное

при числе испытаний n< 30 при числе испытаний 30≤ n<50

где - коэффициент, зависящий от числа испытаний (табличное значение).

Коэффициент вариации:

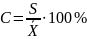
Размах варьирования – разница между наибольшей и наименьшей величинами в выборке

Абсолютная ошибка выборки где t – коэффициент Стьюдента, выбираемый по таблице в зависимости от числа испытаний.

Относительная ошибка выборки

Сводные характеристики выборки при большом числе испытаний (n?50)

Сначала находят разницу между максимальной и минимальной величинами, т.е. размах варьирования по формуле (6). Далее определяют классовый интервал

где n_k - число классов. Желательно, чтобы 7<n_k<20. Желательно, чтобы величина k была кратной 5 или 10. Разбивают полученные значения на классы, которые располагаю по возрастанию значений, и результаты представляют в таблице

Границы классов	Среднее значение в классе	Число значений в классе (частота попадания в класс)		Условное отклонение 	ni	ni2
		ni	ni,%

Напротив наибольшего числа значений в классе отмечают условное отклонение  , от него увеличивающиеся на единицу отклонения: вниз – положительные, вверх – отрицательные. Среднее значение выборки определяют по формуле: где Х – среднее значение в классе при  = 0; k – классовый интервал; n – общее число измерений. Среднее квадратическое отклонение

Сводные харктеристики для партии материала.

Для исследователя важно знать точность и надежность оценки каждого определенного параметра, представления о которых дают доверительные интервалы.

Доверительный интервал – это интервал от Х- ε до Х+ε, который покрывает неизвестный параметр распределения с заданной доверительной вероятностью .

Доверительная ошибка ε = характеризует случайную ошибку параметра распределения. Чем меньше значение ε, тем больше точность оценки Х.

Доверительной вероятностью называется вероятность того, что истинное значение многих числовых характеристик Х лежит в этом интервале Х-ε < < Х+ε.

Абсолютная доверительная ошибка определяется по формуле: где t и -коэффициенты Стьюдента, при доверительной вероятности γ=0,95, определяются по таблице. S-среднее квадратическое отклонение n-число испытаний

Относительная ошибка опыта определяется по формуле δ=

Для снижения ошибки увеличиваем кол-во испытаний, применяя формулу

Доверительный интервал ограничен нижней и верхней доверительными границами, в его пределах с некоторой вероятностью находится сводная характеристика или

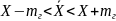
При определении доверительного интервала возможно использование одно- и двусторонних границ:

Для односторонней границы:

Нижняя граница: Верхняя граница:

Для двусторонних границ:

Нижняя граница: Верхняя граница: