Вариант 17

ЗАДАЧА 1

Математический маятник, состоящий из нити длиной 1 м и свинцового шарика радиусом 2 см, совершает гармонические колебания с амплитудой 6 см. Определить скорость шарика при прохождении им положения равновесия. Построить график зависимости возвращающей силы от времени, если в начальный момент времени маятник находился в положении равновесия.

ЗАДАЧА 2

В колебательном контуре, содержащем катушку с индуктивностью 180 мГ и конденсатор емкостью 2 мкФ, были возбуждены затухающие колебания. Амплитуда силы тока этих колебаний уменьшилась в три раза за 2,5 мс. При этом амплитуда силы тока оказалась равной 40 мА. Найдите волновое сопротивление контура и его добротность. Постройте график убывания амплитуды силы тока в контуре в пределах удвоенного времени релаксации.

ЗАДАЧА 3

Частица участвует одновременно в двух гармонических колебаниях происходящих вдоль одного направления. Частота 7 Гц одинакова для обоих колебаний, начальные фазы имеют значения рад и рад, а амплитуды соответственно равны 10 см и 15 см. Напишите уравнения исходных колебаний, Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение.

Примечание. Уравнение траектории не зависит от

начальных фаз колебаний, но зависит от их разности.

Вариант 18

ЗАДАЧА 1

Когда в идеальном колебательном контуре, содержащем катушку индуктивности и два последовательно соединенных конденсатора емкостями 0,2 мкФ и 0,4 мкФ возбудили собственные колебания, то их частота оказалась равной 1,5 кГц. Найдите уравнение для тока в контуре, если конденсатор емкостью 0,4 мкФ отключить, оставшийся конденсатор зарядить до напряжения 50 В и подключить его к прежней катушке индуктивности. Постройте график зависимости электрической энергии в колебательном контуре от времени.

ЗАДАЧА 2

Шар массой 500 г подвешен к пружине жесткостью 20 Н/м и совершает упругие колебания в некоторой среде. Начальная амплитуда колебаний 8 см. Логарифмический декремент затухания 0,05. Сколько колебаний совершит шар пока амплитуда колебаний уменьшится в два раза? За какое время это произойдет? Постройте график зависимости смещения шара от времени для первых пяти колебаний.

ЗАДАЧА 3

Частица участвует одновременно в двух гармонических колебаниях, совершающихся по взаимно перпендикулярным направлениям. Заданы частоты колебаний =8 Гц, =16 Гц, их амплитуды =9см, =14см и начальные фазы рад и - рад. Напишите уравнения исходных колебаний. Найдите уравнение траектории результирующего движения в координатах ХОУ и постройте ее график. Укажите на графике положение частицы в начальный момент времени и направление движения по траектории.

Вариант 19

ЗАДАЧА 1

Математический маятник массой 0,2кг имеет в любой момент времени одну и ту же полную энергию, равную 1 мДж. Найти амплитудное значение импульса маятника. Построить график зависимости кинетической энергии маятника от времени, если длина маятника 1 м, в начальный момент времени смещение маятника равно половине амплитуды.

ЗАДАЧА 2

Колебательный контур состоит из катушки с индуктивностью 60 мГ и сопротивлением 4 Ом и конденсатора. В начальный момент энергия заряженного конденсатора была 0,35 мДж, и он был заряжен до напряжения 25 В. Начальный ток был равен нулю. Напишите уравнение колебаний для заряда на одной из обкладок. Постройте график зависимости заряда от времени.

ЗАДАЧА 3

Частица участвует одновременно в двух гармонических колебаниях, происходящих вдоль одного направления. Частота 3 Гц одинакова для обоих колебаний, начальные фазы имеют значения рад и 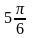рад, а амплитуды соответственно равны 14 см и 14 см. Напишите уравнения исходных колебаний. Найдите амплитуду и начальную фазу результирующего колебания. Запишите его уравнение. При каких условиях сложение двух колебаний приводит к: а) исчезновению колебательного движения? б) удвоению амплитуды?

Примечание. Уравнение траектории не зависит от

начальных фаз колебаний, но зависит от их разности.