2.2.3. Определение предельных допускаемых напряжений

Допускаемые напряжения при проверке на прочность при кратковременных перегрузках ([1],стр.180,табл.9.16):

;

.

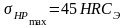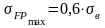Извлечение из таблицы ([4],стр.271,табл.10.15):

сталь 40ХН - 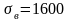МПа;

сталь 40Х - 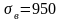МПа;

Получаем 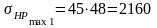МПа;

МПа;

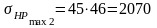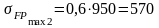МПа;

МПа;

2.2.4. Расчет геометрических параметров передачи

Внешний делительный диаметр конического колеса ([1],стр.162):

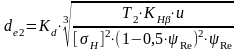
где К_d – числовой коэффициент, К_d = 86,0 для колес с круговым зубом;

u – передаточное число передачи, u = 2,8;

T₂ – вращающий момент на колесе;

К_H – коэффициент неравномерности распределения нагрузки по длине зуба;

_Re - коэффициент длины зуба;

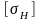- допускаемое контактное напряжение;

Принимаем К_H =1,45 ([1],стр.180,табл.9.17);

_Rе=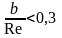 , рекомендуют _Rе=0,285.

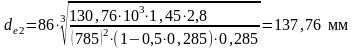
Принимаем по ГОСТ 12289-76 d_e2 = 180 мм ([1],стр.172,табл.9.4);

Основные геометрические характеристики ([1],стр.179,табл.9.15):

Внешний делительный диаметр шестерни: ;

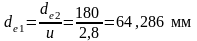Примем число зубьев шестерни z₁ = 25,

тогда число зубьев колеса z₂ = u  z₁ = 2,8  25 = 70;

Внешний окружной модуль ;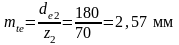

Внешнее конусное расстояние

;

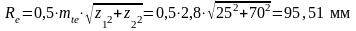Ширина зубчатого венца b = _Re  R_e = 0,285  95,51 = 27,2 мм,

Принимаем b =28 мм;

Среднее конусное расстояние

R = R_e – 0,5  b = 95,51 – 0,5∙28=81,51 мм;

Угол делительных конусов ₂ = arc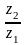tg = arctg 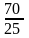= 702037,

₁ = arc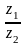tg = arctg 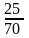= 193923,

Средний нормальный модуль m_n = m_te(1 – 0,5  _re)cos,

принимаем cos = 35^o, тогда m_n = 2,8(1 – 0,50,285)cos35^o = 1.50 мм;

Внешняя высота зуба:

h_e = 2m_te(cos  + 0,1) =22,57(cos35^o + 0,1) = 4,72 мм;

Внешняя высота головки зуба:

h_ae1= m_tecos (1+x₁) = 2,57cos35^o(1+0,2587) = 2,65 мм;

h_ae2= 2m_tecos  - h_ae1 = 22,57 cos35^o – 2,65= 1,56 мм;

где: x₁ – коэффициент радиального смещения:

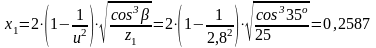мм;

Внешняя высота ножки зуба

h_fe1 = h_e – h_ae1 = 4,72 – 2,65 = 2,07 мм;

h_fe2 = h_e – h_ae2 = 4,72 – 1,56 = 3,16 мм;

Средний делительный диаметр

шестерни ;

колеса ;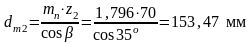

Внешний диаметр вершин зубьев

d_ae1 = d_e1 + 2  h_ae1  cos ₁ = 64,286 + 2  2,65  cos 193923 = 69,27мм;

d_ae2 = d_e2 + 2  h_ae1  cos ₂ = 180+ 2  1,56  cos 702037 = 181,05 мм.

2.2.5. Определение усилий в зацеплении

1. Окружная сила на среднем диаметре:

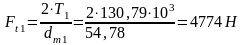
2. Радиальная сила на шестерне , равная осевой силе на колесе :

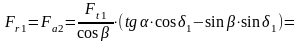
Н;

3. Осевая сила на шестерне 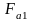, равная радиальной силе на колесе :

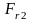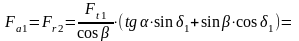
Н

где - угол профиля.

2.2.6. Проверочный расчет по контактным напряжениям

Уравнение для проверочного расчета на контактную прочность активных поверхностей зубьев ([8],стр.127):

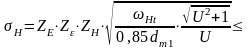
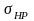
где 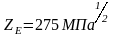([8],стр.127);

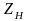- коэффициент, учитывающий форму сопряженных поверхностей;

;

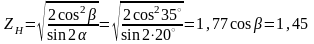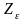- коэффициент, учитывающий суммарную длину контактных линий

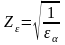
где 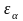- коэффициент торцевого перекрытия:

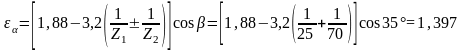
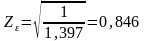
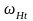- удельная расчетная окружная сила:

,

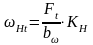где - коэффициент нагрузки:

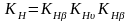
где К_Нβ =1,18 – коэффициент, учитывающий распределение нагрузки по ширине венца ([4],стр.263, рис.10.35);

К_Нα =1,1 - коэффициент, учитывающий распределение нагрузки между зубьями ([1],стр.178, табл.9.12);

К_Нυ - коэффициент, учитывающий внутреннюю динамику передачи, определяется в зависимости от скорости окружной шестерни степени точности передачи:

=

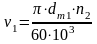Степень точности – 7 ([9],стр.52,табл.4.2.14);

К_Нυ=1,02 ([9],стр.51,табл.4.2.8);

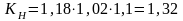
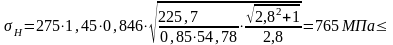
Расчет показывает, что прочность по контактным напряжениям обеспечена.