Моделювання гнучкості.
Гнучкість - це властивість обернена керуванню, тобто спроможність бути керованим.
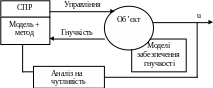
Гнучкість - це спроможність адаптуватися в умовах обурення.
Гнучкість має одиниці виміру, за умови якщо ми її представимо в вигляді вектора:
технологічна гнучкість Kf
організаційна Kf
структурна Kf
інтерактивна Kf
еволюційна Kf
машинна Kf
Технологічна гнучкість – спроможність рівня автоматизації (РА) адаптуватися в умовах номенклатури виробу , що змінюється.
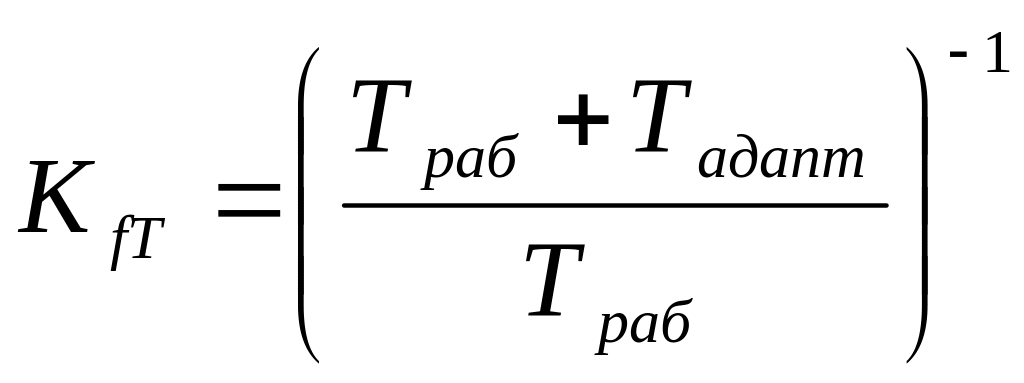
Структурна гнучкість - спроможність РА бути взаємозамінним.
Організаційна гнучкість – спроможність РА бути незалежним, автономним від інших РА.
Коефіцієнт автоматизації Шаумена:
Інтерактивна гнучкість - спроможність швидкого прийняття рішень за допомогою ПК і технології.
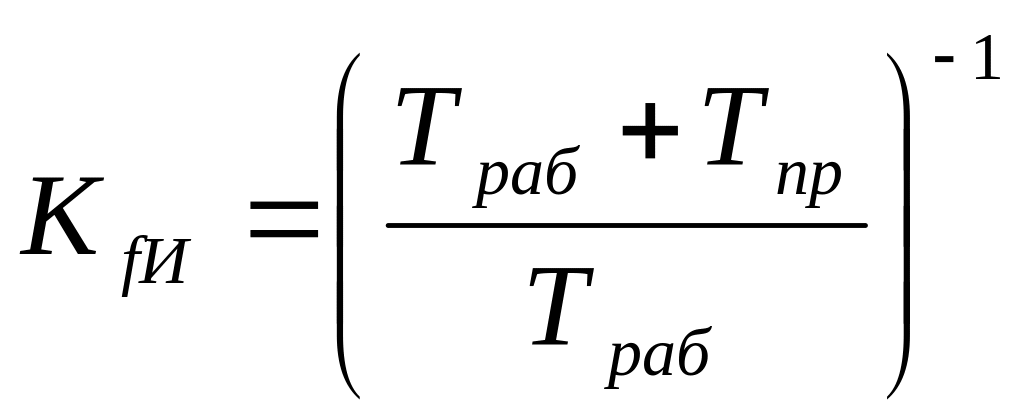
Еволюційна гнучкість - спроможність адаптуватися в умовах розвитку технологій. Будь-яка модель не повинна бути тупиковою.
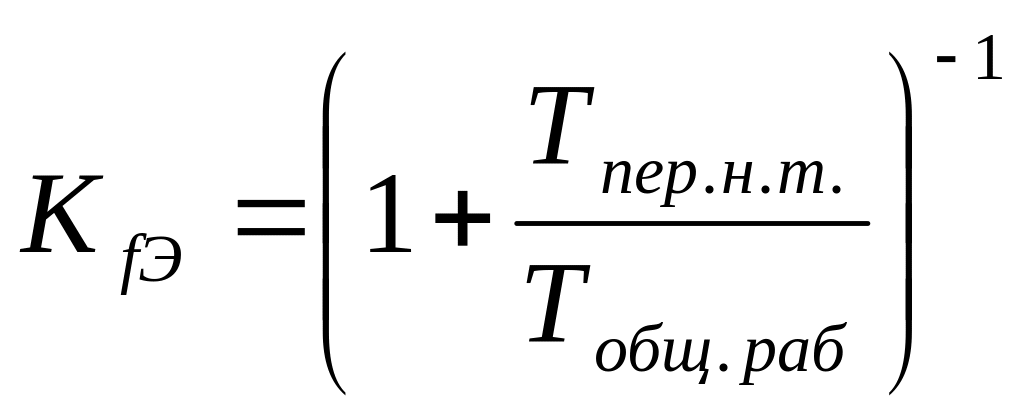
Машинна гнучкість – спроможність до недорогої адаптації.
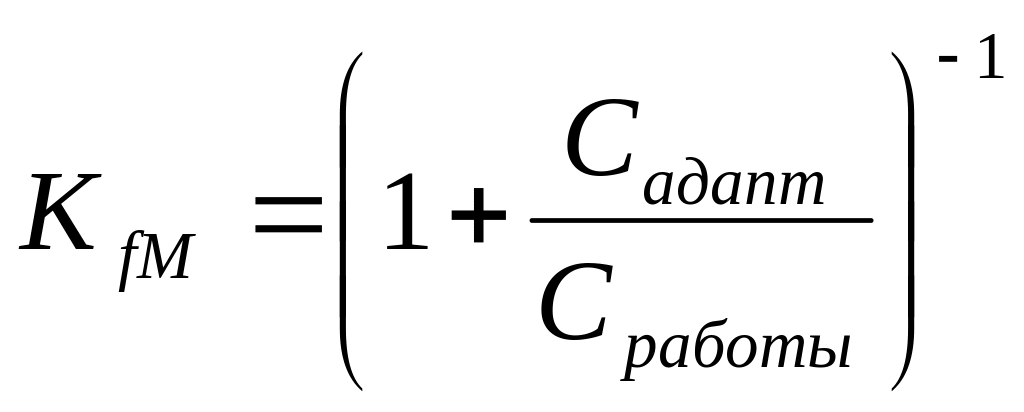
Далі працює один із методів технічного пошуку.
Один із варіантів моделі забезпечення гнучкості:
- коефіцієнт лінійної згортки;
Приклад – забезпечення гнучкості:
Фірма організовує транспортування своєї продукції для СМР, що описуються за допомогою сітьового графіка.
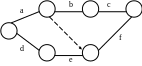
Для кожної роботи (a, b, c, d, e, f) вирішена задача комплектації (робота a використовує 1, 2 об'єкт ...).
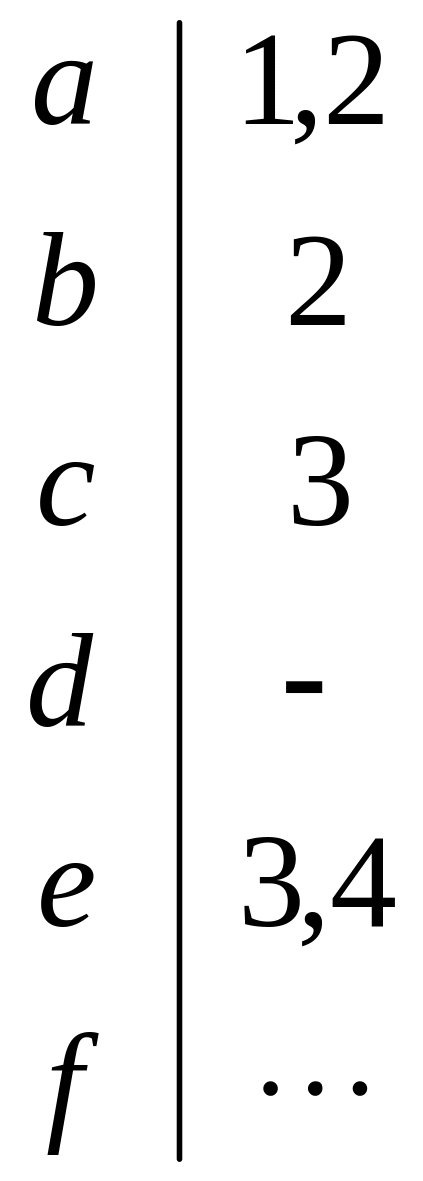
Розрахувавши сітьовий графік методом Дейкстра – I, отримаємо результат:
Перетворимо трансформуванням t у T:
Будь-який об'єкт має склад (естакади, зони, контейнери, площадки):
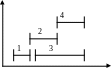
4) Отримаємо резерви часу, виходячи з площі:
5) Маючи резерви часу, здійснюємо:
6) Організація постачань (будується в масштабі циклограма):
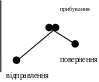
Приклад 2:
Задано задачу (схожа на транспортну).
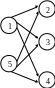
Необхідно організувати прямування постачань в залежності від потреби на основі інтервальних графіків. Час переміщення задано в таблиці.
-
Відправлення
Час повернення
-
3
4
4
-
2
-
-
-
3
3
-
-
-
4
3
-
-
-
2
-
4
5
3
-
На основі заявок:
|
Інтервал |
Звідки \ куди |
1 |
5-10 |
1-2 |
2 |
6-12 |
1-3 |
3 |
9-14 |
5-2 |
4 |
12-20 |
1-4 |
5 |
10-18 |
5-4 |
Потрібно організувати постачання таким чином, щоб одержати мінімальну кількість автомашин і максимальні резерви часу.
Використовуючи задані резерви часу:
Рішення: графік має такий вигляд :
X |
Звідки \ куди |
tвідпр. |
комплект |
tприбуття |
Макс. інтервал |
||
от |
до |
от |
до |
||||
1 |
1/2 |
2 |
4 |
1 |
5 |
7 |
5-10 |
2 |
1/2 |
7 |
9 |
2 |
10 |
12 |
6-12 |
3 |
1/4 |
13 |
16 |
4 |
17 |
20 |
12-20 |