Правило множників Лагранжа.

Оптимум знаходиться для умови , якщо всі обмеження рівні нулю (прирівняні).

х² + у² + z² min

x + y +3z = 2

5x + 2y + z = 5

Ідея Лагранжа: завжди можна звернути всі цільові функції й обмеження в одну функцію, тобто якщо ми маємо:

,

то завжди можна ввести нові змінні _i і записати нову функцію Лагранжа: .

Продовжувати рішення потрібно аналогічно класичному методу (1 ЦФ: без умовної оптимізації).

= x² + y² + z² + ₁(x + y + 3z - 2) + ₂(5x + 2y + z - 5)  min

Розмірність 5.

= 2x + ₁ + 5₂ = 0 (*)

= 2y + ₁ + 2₂ = 0

= 2z + 3₁ + ₂ = 0

= x + y + 3z - 2 = 0

= 5x + 2y + z - 5 = 0

Далі вирішуємо систему й одержуємо результат:

(x, y, z, ₁, ₂₎ = (0.804, 0.3477, 0.2855, -0.0869, -0.3043).

Потім рахуємо цільову функцію:

f(0. 804, 0. 3477, 0. 2855) = ...

Беремо будь-яку точку округи, наприклад:

F0(0. 804, 0. 3477, 0. 2855) і визначаємо (мінімум або максимум):

в залежності від того f>f0 ?

Знак можна визначити також використовуючи матрицю Гессе. Записується визначник, розмірністю 5х5. (*)

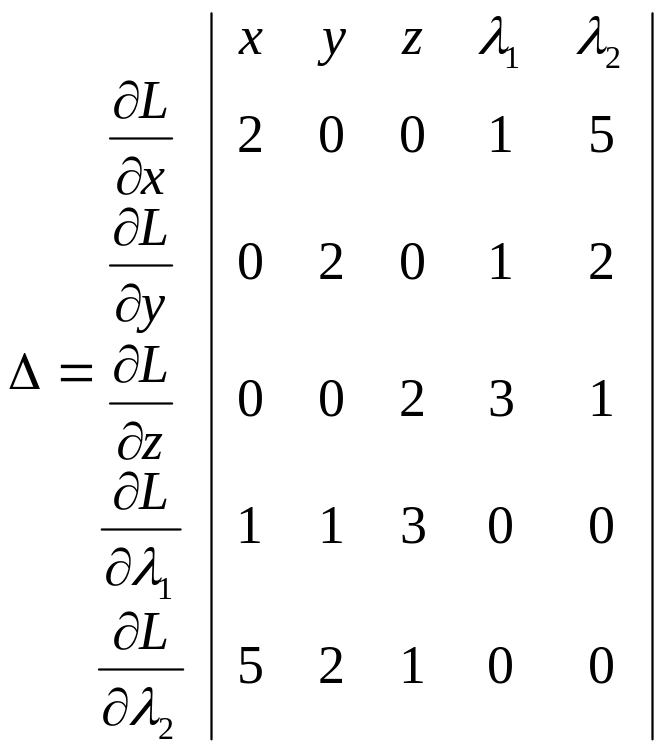=640 обчислюється значення визначника

Якщо визначник більше нуля значить це мінімум.

Узагальнене правило Лагранжа.

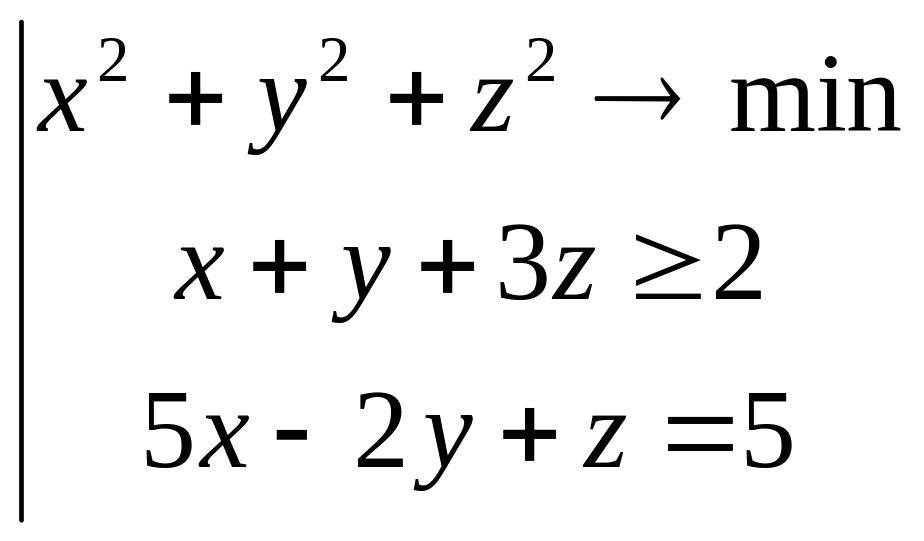
Ідея: рішення задачі полягає в тому, що потрібно поступово будувати функцію Лагранжа, і на кожній ітерації необхідно знаходити рішення по Лагранжу і підставляти в обмеження , що залишилися.

Якщо рішення задовольняє обмеженням, то оптимальне рішення знайдене, якщо ні - в функцію Лагранжа додається одне з обмежень. Ітераційний процес продовжується.

Опис алгоритму.

1) Будуємо функцію Лагранжа на основі цільової функції й обмежень типу рівності = x² + y² + z² + ₁(5x - 2y + z - 5)  extr і вирішуємо задачу безумовної оптимізації

= 2x + 5₁ = 0

= 2y - 2₁ = 0

= 2z + ₁ = 0

= 5x - 2y + z - 5 = 0 R=(..., ..., ...)

Після рішення підставляємо отримані x, y, z в обмеження , що залишилися, якщо задовольняє, то рішення знайдено. Інакше:

2) будуємо функцію Лагранжа з урахуванням такого обмеження, що не задовольняє попередньому рішенню. Проводиться умовна оптимізація = x² + y² + z² + ₁(x + y + 3z - 2) + ₂(5x + 2y + z - 5)  extr.

Генерується система з п'яти рівнянь і вирішується. І так далі, доки не будуть розглянуті всі обмеження.

Примітка. Якщо на етапі рішення системи рівнянь рішення відсутнє, то з використанням методу множників Лагранжа рішення відсутнє. У цьому випадку можливо 2 висновки:

• рішення дійсно відсутнє, ОДР не обмежена зверху або знизу;

• рішення є, але використовуючи даний метод, знайти його не можна.

Некомп’ютерні методи. Умова Куна - Таккера.

Ціль: аналогічно приведенню нерівностей до рівностей (алгоритм приведення до канонічного виду) у задачах ЛП здійснюється додаванням нових штучних змінних.

здійснюється так:

1) запровадження нових невід’ємних змінних S1, ... , Sn.

2) додавання квадратів змінних S1, ... , Sn (щоб при диференціюванні змінна не пропала) і формування нової функції Лагранжа.

На основі часткового диференціювання одержуємо систему:

Аналізуючи останнє обмеження:

Якщо _i  0, то Si = 0 і gi(x) = 0.

Звідси умова Куна – Таккера має вид:

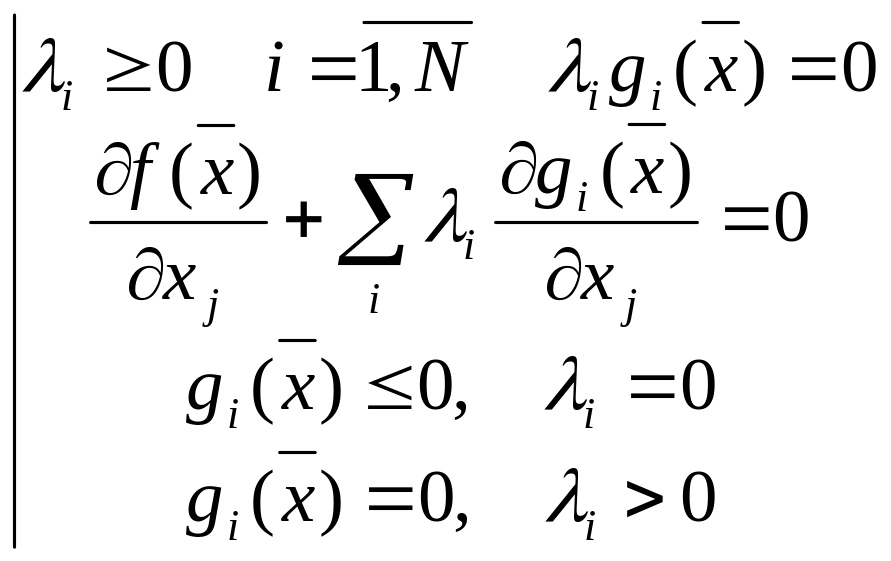
Питання в тому, який оптимум ми шукаємо.

Тип оптимуму	f(x)	gi(x)	i
Максимум	Увігнута	Випукла	0
		Увігнута	0
		Лінійна	Не має обмежень
Мінімум	Випукла	Випукла	0
		Увігнута	0
		Лінійна	Не має обмежень