Задача конденсування мережі. Алгоритм Гоморі-Xу.

М ережу можна перетворити в остов:

Переписати у виді матриці.

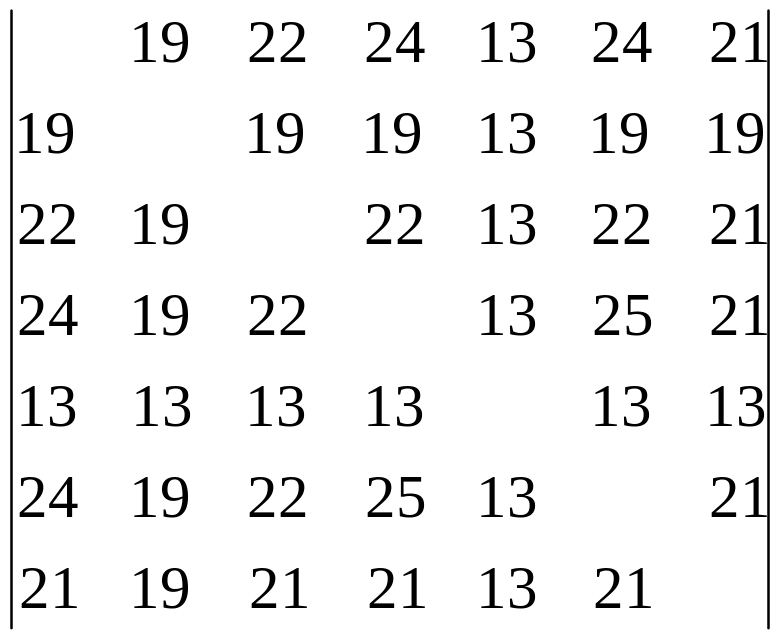
1) За даною матрицею можна зробити такі висновки, з метою забезпечення максимуму потоку і надійності мережі:

стік у точці 4

насос у точці 6

2) Перебираючи S і T за допомогою алгоритму Дейкстра можна проаналізувати, де найбільше напружені вузли і дуги.

Ідея алгоритму: використовується поняття розріз.

Розріз - це мінімальна множина дуг, що дозволяє відключити вузол S або T і зробити мережу незв'язною.

Пропускна спроможність розрізу - це сума всіх пропускних спроможностей вхідних дуг.

Мінімальний розріз - це розріз, що має мінімальну суму. Дорівнює максимальному потокові або пропускній спроможності мережі.

Приклад: Задано мережу. Необхідно її розрахувати.

М атриця суміжності:

І = 134  = 3

І І = 124  = 4

І І І = 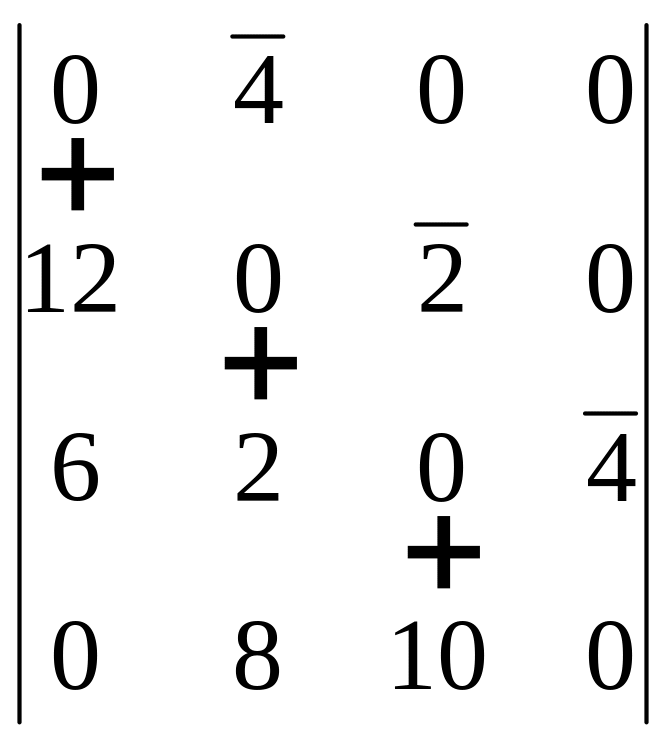1234  = 2

І V =

Порівнюючи матрицю І та ІV визначаємо наступну матрицю f:

f = F=9

II^-й метод: використання теореми про мінімальний розріз.

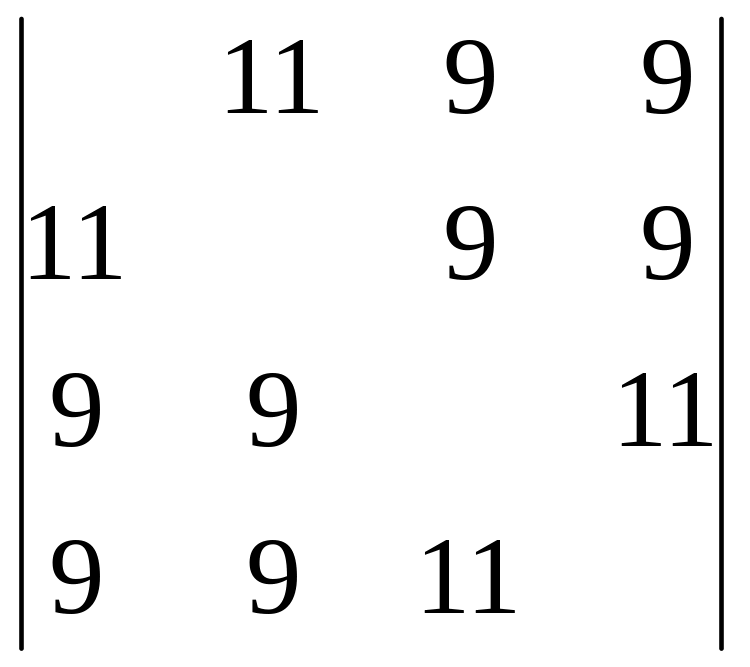
III^-й метод: алгоритм конденсування:

Алгоритм складається з (N-1) ітерацій. Для кожної ітерації ми робимо стиск, розглядаючи при цьому довільну пару. i=1. .N-1 kl mk nm

12 F = 11 = 8+3

31 F = 9 = 3+2+4

Вузли по одну сторону  перехід до іншої мережі (стискуємо).

43 F = 11 = 7+4

Опис алгоритму.

1. Вихідне остовне дерево містить порожню множину дуг і вузлів.

2. Вибираємо пов'язану пару S і T, що випливає.

3. Визначаємо мінімальний розріз і максимальний потік із S у T за допомогою алгоритму Дейкстра або за теоремою про мінімальний розріз.

4. Розріз представлено гілкою остова між групами вузлів. Вага гілки дорівнює пропускній спроможності мінімального розрізу.

5. Якщо розглянутий (N-1) вузол, таким чином остов побудований. Якщо немає, то:

а) конденсуємо в один вузол кожну пов'язану пару, раніше обраних S і T (конденсування виконується в тому випадку, якщо вузли лежать по одну сторону розрізу);

б) вибираємо таку пару S і T, де Т - вузол, що входить у попередню пару;

в) перехід до пункту 3.

Приклад.

1 ) 25 F = 13 = 7+4+2

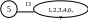
2) 12 F = 19 = 8+5+4+2

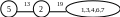
3) нова мережа:

4) 41 F = 24

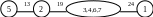
5) 34 F = 22

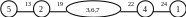
6) 63 F = 22

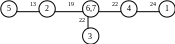
7) 76 F=19

Рішення багатокритеріальних задач.

Векторна оптимізація.

Загальна постановка.

тобто, існує множина цільових функцій і необхідно вирішити задачу: Z = (Z1,. ., Zn) - вектор.

І. Метод лінійної згортки: в якому всі цільові функції приводяться до однієї цільової функції за допомогою коефіцієнтів:

а) проранжувати (оцінити) кожну цільову функцію, порахувати _i (змінні Лагранжа);

б) привести до однієї одиниці виміру (якщо f - стільці, то  - гроші);

в) привести всі Z до одного знаку (множенням правої або лівої частини на -1);