Последовательно-параллельные ацп

Последовательно-параллельные АЦП - это компромисс между параллельными и последовательными АЦП, т. е. желание получить максимально возможное быстродействие при минимальных затратах и сложности.

На рисунке 7 показан для примера двухступенчатый АЦП. В многоступенчатых преобразователях процесс преобразования разделен в пространстве.

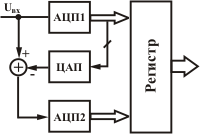
Рис. 7 - Двухступенчатый АЦП

Для примера на рисунке изображен двухступенчатый АЦП. АЦП1 (верхний) осуществляет "грубое" преобразование входного сигнала в старшие разряды. Сигналы с выхода первого АЦП поступают на выходной регистр и одновременно на вход быстродействующего ЦАП. Кружочек с плюсиком - это сумматор, но в данном случае вычитатель. Цифровой код преобразуется ЦАП в напряжение, которое вычитается из входного в этом самом кружочке с плюсиком. Разность напряжений преобразуется с помощью АЦП2 в коды младших разрядов. Регистр для упрощения можно выкинуть. В таких схемах ЦАП чаще всего выполняется по схеме суммирования токов с помощью дифференциальных переключателей, но могут быть построены по схеме суммирования напряжений.

Требования к точности АЦП1 выше, нежели ко второму. Оба АЦП параллельного типа. Допустим, и тот, и другой 4-х разрядные, в каждом используется по 16 компараторов. В итоге получается 8-ми разрядный АЦП всего на 32 компараторах, тогда как при построении по параллельной схеме понадобилось бы 2⁸ - 1 = 255 шт. Быстродействие примерно раза в два хуже. Помимо этого бывают многотактные последовательно-параллельные и конвейерные АЦП. У них несколько иная структура. К примеру, многотактные преобразователи работают с различным шагом квантования, т. е. в преобразователе процесс преобразования разделен во времени. В один момент времени формируются старшие разряды, в другой момент времени шаг квантования уменьшается и формируются младшие разряды.

Большое распространение получил способ с использованием так называемого сигма-дельта модулятора. Про это будет отдельная глава.

Цифровой фильтр (ЦФ) - устройство, пропускающее, либо подавляющее заданные в цифровой форме сигналы в определенной полосе частот. В отличие от аналоговых фильтров, у которых входной сигнал изменяется непрерывно, в цифровых входной сигнал представляется в дискретной форме, т. е. принимает каждый раз новое значение через интервал дискретизации. Величина, обратная этому интервалу, - частота дискретизации, в большинстве практических случаев должна превышать полосу частот входного сигнала в 4...8 раз.

Преимущества ЦФ перед аналоговыми следующие:

• стабильность характеристик, связанная с тем, что частота дискретизации задается кварцевыми генераторами;

• простота перестройки частотной характеристики (обычно либо перестраивают частоту дискретизации, либо вводят новые значения каких-либо цифровых кодов);

• возможность в одном устройстве выполнить сразу несколько ЦФ (либо с одинаковыми частотными характеристиками для многоканальных систем, либо даже с разными характеристиками - гребенки фильтров).

ЦФ можно использовать для высококаКчественной обработки сигналов в устройствах звуковоспроизведения и магнитной записи, при синтезе и анализе речевых сигналов, в электронных музыкальных инструментах (ЭМИ) и т. д.

На рис. 1 показана схема простейшего ЦФ, состоящего из сумматора и устройства задержки во времени (которое можно реализовать на запоминающем устройстве). Если входной сигнал ЦФ - синусоидальный с частотой f, а задержка во времени составляет половину периода этого сигнала, то на сумматоре сигналы вычитаются и входной сигнал ЦФ равен нулю. То же самое будет, если задержка составит 1,5 периода, 2,5 периода и т. д. Если задержка будет равна нулю или целому числу периодов сигнала, то на сумматоре будет чистое суммирование, на выходе ЦФ амплитуда будет равна удвоенной входной амплитуде. На рис. 2 сплошной линией показана частотная характеристика простейшего ЦФ. Если вместо сумматора установить вычитатель, то образуется частотная характеристика, показанная на рис. 2 пунктирной линией.

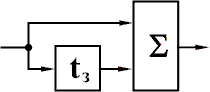
Рис. 1 - Простейший цифровой фильтр

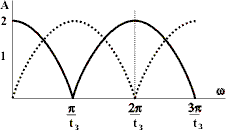
Рис. 2 - Частотная характеристика простейшего цифрового фильтра

В более общем случае ЦФ состоит из набора устройств задержки и сумматора, причем сдвинутые во времени сигналы суммируются с различными коэффициентами передачи (весами) a₀, a₁, a₂... (рис. 3). Говорят, что импульсная характеристика ЦФ состоит из набора сдвинутых во времени отсчетов входного сигнала, а поскольку количество этих отсчетов определяется количеством устройств задержки, то импульсная характеристика ограничена во времени. Поэтому такие фильтры называют фильтрами с конечной импульсной характеристикой или КИХ-фильтрами.

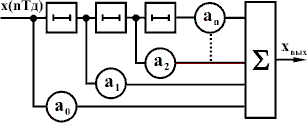
Рис. 3 - Структура КИХ-фильтра

КИХ-фильтры

На рис. 4.а показано, как изменяется частотная характеристика КИХ-фильтра при суммировании двух отсчетов с равными весами (то же, что на рис. 2 сплошная линия) и при суммировании шести отсчетов (рис 4.б), у которых весовые коэффициенты изменяются по закону, показанному на рис. 4.г, где а₀ = 1; а₁ = 0,83; а₂ = 0,41; а₃ = 0; а₄ = -0,2; а₅ = -0,16.Для сравнения на рис. 4.в показаны отсчеты с единичным весом.

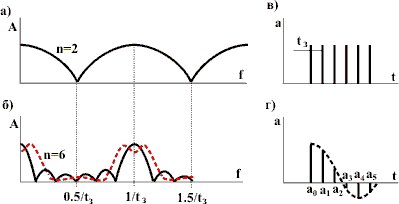
Рис. 4 - Частотная характеристика КИХ-фильтра при равновесном (а, в) и разновесном (б, г) суммировании

Как видно, характеристика становится более прямоугольной и исчезают пульсации. Но при этом основной дефект КИХ-фильтров - чатотная характеристика повторяется через интервал частот f = 1/t_з.

От этого недостатка свободны ЦФ с бесконечной импульсной характеристикой - БИХ-фильтры

БИХ-фильтры

Структура такого фильтра показана на рис. 5. Если на вход БИХ-фильтра подать отсчет единичной амплитуды, то выходные отсчеты будут формироваться как сумма задержанных отсчетов с различными весами а₁, а₂, ..., которые снова через сумматор подаются на устройства задержки. Процесс этот длится бесконечно, откуда название ЦФ. Следует отметить, что все весовые коэффициенты должны быть меньше единицы, иначе процесс на выходе ЦФ будет бесконечно нарастать по амплитуде.

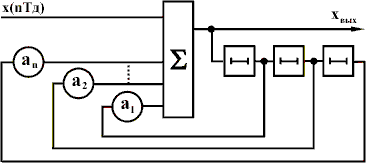
Рис. 5 - Структура БИХ-фильтра

На рис. 6 сплошной линией показана частотная характеристика БИХ-фильтра, у которого только один весовой коэффициент а₁ = 0,875. Но уже с двумя весовыми коэффициентами (а₁ = 0,875, а₂ = -0,02) частотная характеристика фильтра нижних частот получается гораздо более прямоугольной (на рис. 6 - штриховая линия).

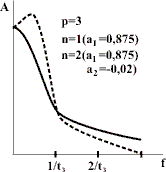
Рис. 6 - Частотные характеристики БИХ-фильтра

Применение в ЦФ весовых коэффициентов, не равных единице или нулю, требует применения умножителей. Поэтому в последнее время ЦФ чаще реализуют программным путем в ЭВМ. В программу записывают все необходимые математические операции и задержки во времени. Такую программу (состоящую из сотен и тысяч элементарных машинных операций) необходимо выполнять для каждого отсчета входного сигнала, поэтому на ЭВМ можно построить только сравнительно низкочастотные ЦФ. При аппаратной реализации можно получить более высококачественные ЦФ, однако потребуются десятки микросхем.

Расчет ЦФ с различными частотными характеристиками - сложная математическая задача, которой посвящен ряд специальных руководств.

Разновидностью БИХ-фильтра является синхронный цифровой фильтр. Аналоговый вариант синхронного фильтра (рис. 7.а) представляет собой цепочку с одним резистором и набором конденсаторов С1-С4, подключаемых через ключи К1-К4 по очереди с помощью импульсов U1-U4 (рис. 7.б). Если частота входного сигнала совпадает с частотой коммутации кондеров f_к, то выходное напряжение достигает максимального значения, что соответствует резонансу. При перестройке частоты коммутации перестраивается и частота резонанса. Ширина полосы частот определяется постоянной времени RC.

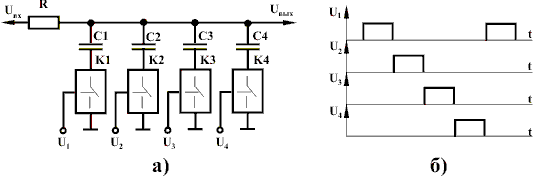
Рис. 7 - Аналоговый вариант синхронного фильтра (а) и импульсы управления (б)

Цифровой вариант синхронного фильтра показан на рис. 8.

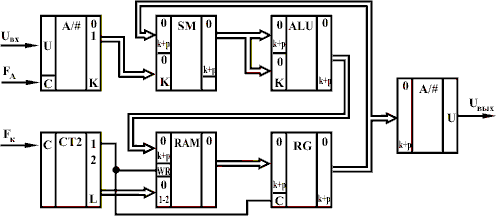
Рис. 8 - Цифровой вариант синхронного фильтра

Аналоговый входной сигнал U_вх поступает на аналого-цифровой преобразователь, с выхода которого цифровые коды сигнала с частотой дискретизации f_д поступают на сумматор SM, на второй вход которого поступают коды с выхода регистра RG (вспомним, что сумматор с регистром образуют сумматор-накопитель). Но после сумматора включено арифметико-логическое устройство ALU, работающее в режиме вычитания, причем на второй вход подана часть того, что подано на первый вход. В результате получается процедура 1 - 1/n = (n - 1)/n. Например, n=8, тогда 1-1/8=7/8=0,875, т. е. амплитуда сигнала несколько уменьшается. При n=8 достаточно код сигнала на втором входе сдвинуть на три разряда вниз.

Предположим, что оперативного запоминающего устройства RAM нет. Тогда сумматор, АЛУ и регистр образуют сумматор-накопитель с затуханием. В обычном сумматоре-накопителе, если снять со входа сигнал, то накопленный результат будет просто храниться. В описанном устройстве результат будет постепенно убывать, как это происходит в RC-цепи, т. е. сумматор, АЛУ и регистр являются цифровым аналогом RC-цепи. Чем меньшая часть сигнала вычитается в АЛУ, тем больше эквивалентная постоянная времени цифровой RC-цепи.

Теперь осталось только добавить запоминающее устройство с адресным счетчиком для хранения результатов по m каналам и получим синхронный фильтр аналогичный рис. 7.а. Но если в аналоговом синхронном фильтре с увеличением числа кондеров нарастает сложность устройства, то в цифровом число эквивалентных кондеров определяется объемом памяти запоминающего устройства, следовательно, может быть большим без увеличения объема устройства.

На выходе синхронного цифрового фильтра установлен цифро-аналоговый преобразователь, поэтому выходной результат, так же как и входной, получается аналоговым.

В предыдущей главе мы рассмотрели Цф с реализацией во времени. Другой класс ЦФ - это ЦФ с частотной реализацией. В отличие от временных методов, где анализируется каждый отсчет сигнала, в ЦФ с частотной реализацией анализируется набор из n отсчетов. Существуют различные алгоритмы обработки этих n отсчетов, из которых наиболее часто применяют алгоритм дискретного преобразования Фурье (ДПФ) и быстрого преобразования Фурье (БПФ).

ДПФ-фильтры

Алгоритм ДПФ состоит в умножении значений входных отсчетов на значения опорного сигнала синусоидальной формы заданной частоты и накоплении суммы этих произведений. Поскольку входной сигнал дискретизирован, то и опорный сигнал представляется в виде m дискретных значений на периоде (m-точечное ДПФ). Минимальное число m=2, при этом опорный сигнал принимает всего два значения (+1 и -1), и умножение на такой сигнал сводится к перемене знака отсчета входного сигнала. На рис. 1 этот процесс показан для n=8. Если входной сигнал имеет ту же частоту, что и опорный, то результат накопления зависит от взаимной фазировки входного и опорного сигналов. Чтобы устранить эту зависимость, ЦФ делают двухканальным - в одном канале опорный сигнал сдвигают по фазе на 90° по отношению к опорному сигналу в другом канале.

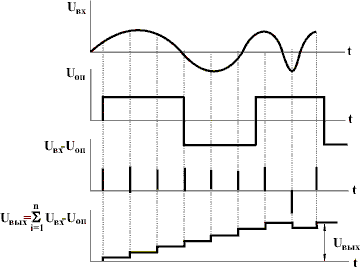
Рис. 1 - Диаграммы сигналов при алгоритме ДПФ

Общая схема ДПФ фильтра показана на рис. 2.