2. Гирокомпасы с автономным чувствительным элементом

2.1 Использование гироскопа в качестве курсоуказателя

2.1.1 Горизонтная система координат и ее вращение

Как было определено и доказано ранее, главная ось свободного гироскопа сохраняет неизменным первоначально заданное направление в инерциальном пространстве.

П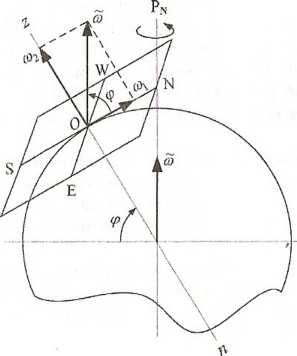 ользуясь свободным ГС можно проследить суточное вращение Земли вокруг ее оси. Так как ось ГС сохраняет свое первоначальное положение, а Земля вместе с наблюдателем вращается, то наблюдатель видит, что ось ГС по­ворачивается относительно плоскостей истинного меридиана и истинного гори­зонта, которые связаны с точкой наблюдателя на поверхности Земли.

Если в первоначальный момент ось ГС находится в меридиане и горизонтальна, то в следующий момент из-за вращения Земли она выйдет из меридиана и одновременно отклонится от горизонта.

Рис. 2.1 Горизонтная система координат

Чтобы гироскоп служил в качестве курсоуказателя, необходимо заставить главную ось ГС непрерывно следовать за меридианом. Но для этого необходимо найти угловые скорости вращения плоскостей меридиана и истинного гори­зонта в зависимости от широты места наблюдателя.

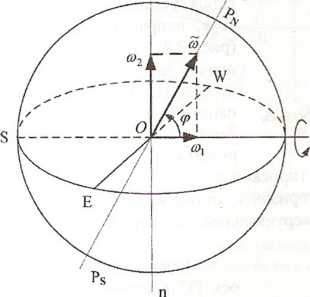На рис. 2.1 изображены сферическая модель Земли и горизонтная система координат.

Земля вращается с запада на восток, совершая оборот за звездные сутки. Землю принято считать шаром с радиусом км. Суточное вра­щение Земли происходит с угловой скоростью сек^-1.

В

Рис. 2.2 Вспомогательная сфера

качестве системы координат выберем горизонтную систему коор­динат ONEn и свяжем ее с некоторой точкой О на поверхности Земли: ось ON направлена по касательной к ме­ридиану на север; ось ОЕ - по касательной к параллели на восток; ось Оn по отвесной линии к надиру. Вследствие суточного вращения Земли будет вращаться и горизонтная система координат ONEn.

Для определения этого вращения построим вспомогательную сферу, поместив в точку О место наблюдателя вместе с горизонтной системой координат в центре этой сферы (рис.2.2). Разложим вектор угловой скорости вращения Земли на составляющие:

- вдоль направления полуденной линии NS;

- вдоль линии отвеса zn.

Вектора , , находятся в плоскости истинного меридиана. Для ве­личин угловых скоростей и имеем соотношения:

- горизонтальная составляющая;

- вертикальная составляющая.

Горизонтальная составляющая суточного вращения Земли показывает, что плос­кость истинного горизонта непрерывно вращается в пространстве вокруг полуденной линии NS так, что восточная половина горизонта опускается, а западная поднимается.

Вертикальная составляющая суточного вращения Земли показывает, что для наблюда­теля, расположенного в северной широте, плоскость истинного меридиана вращается в пространстве вокруг отвесной линии так, что северная часть плоскости меридиана непрерывно отходит к западу, а южная - к востоку. Для южного полушария – наоборот [7].

2.1.2 Видимое движение свободного гироскопа

Рассмотрим несколько случаев видимого движения свободного гироскопа, установленного в различных точках земной поверхности.

На рис. 2.3 изображен земной шар, если смотреть на него со стороны северного полюса PN. Стрелкой показано направление вращения Земли.

Пусть в начальный момент (положение 1) гироскоп находится на экваторе, его ось Х-Х горизонтальна и направлена по линии EW Через некоторый промежуток времени Земля повернется на некоторый угол β и ось гироскопа, сохраняя неизменность своего положения в пространстве, отклонится относи­тельно плоскости истинного горизонта на такой же угол β (положение 2). По­ложение 3 гироскоп займет через 6 часов. В этом положении ось Х-Х прибора будет расположена вертикально. Относительно плоскости горизонта в положе­нии 4 она будет снова горизонтальна, а в положении 5 - опять вертикальна.

Это движение гироскопа будет только кажущимся

Рис. 2.3. Видимое движение свободного гироскопа, установленного на экваторе по линии Е-W

(видимым), в действительности же в результате собственного вращения Земли поворачивается плоскость истинного горизонта, а ось гироскопа сохраняет неизменным в пространстве свое первоначальное направление.

Е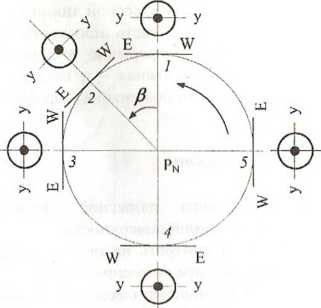 сли главную ось гироскопа, установленного на экваторе, направить по линии NS (рис. 2.4), то вследствие вращения Земли ось ГС будет поворачиваться вокруг оси Х-Х, параллельной оси вращения Земли, и наблюдатель не обнаружит видимого движения ГС. Нетрудно сообразить, что если гироскоп установить на полюсе своей главной осью параллельно плоскости горизонта, то она в течение суток совер­шит полный видимый оборот вокруг вертикальной оси гироскопа в сторону, противоположную вращению Земли.

Рис. 2.4. Видимое движение свободного гироскопа, установленного на экваторе по линии N-S

Если на полюсе главная ось ГС в первоначальный момент расположена вертикально вдоль оси вращения Земли, то наблюдатель не обнаружит видимого движения гироскопа, т.к. ось вращения Земли в этом случае совпадает с осью Х-Х гироскопа.

На рис 2.5 изображен гироскоп, расположенный в некоторой средней северной широте.

Пусть в первоначальный момент (положение 1) ГС находится в меридиане и его ось горизонтальна. Через некоторое время (положение 2) ось Х-Х прибора составит с меридианом наблюдателя некоторый угол а, так как меридиан наблюдателя повернулся в пространстве вместе с Землей, а ось Х-Х гироскопа сохранила свое первоначальное направление. Одновременно с видимым уходом из меридиана главная ось ГС будет подниматься над горизонтом, т.к. последний вращается вместе с Землей, причем его восточная половина непрерывно опускается.

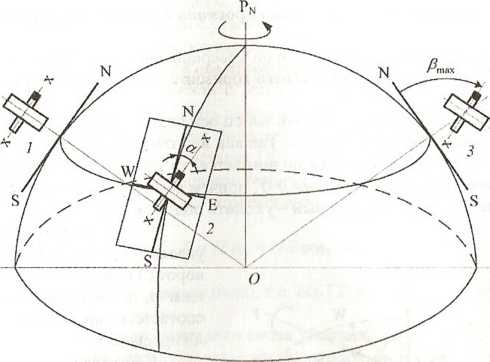
Рис. 2.5. Видимое движение свободного гироскопа, установленного в северной широте

В положении 3 ось Х-Х гироскопа вновь окажется в плоскости меридиана, но будет поднята над горизонтом на угол .

Таким образом, гироскоп установленный в средней северной широте, обнаруживает уход северного конца главной оси от меридиана к востоку и от плоскости истинного горизонта вверх. Главная ось ГС в данном случае будет совершать видимые для наблюдателя незатухающие колебания с периодом суточного вращения Земли. Это движение только видимое, в действительности же в результате вращения Земли вращаются в пространстве плоскости меридиана наблюдателя и истинного горизонта, причем северная часть меридиана наблюдателя непрерывно отходит от оси Х-Х гироскопа к западу, а восточная половина горизонта опускается.

Рассмотренные ситуации показывают, что только в случае параллельности главной оси ГС оси Земли наблюдатель не обнаружит видимого движения гироскопа.

Итак, становится очевидным, что свободный гироскоп не может быть использован в качестве курсоуказателя, так как его главная ось непрерывно уходит от меридиана и одновременно наклоняется к плоскости горизонта.

Поэтому возникает задача, состоящая в том, чтобы стабилизировать главную ось гироскопа в плоскости истинного меридиана наблюдателя параллельно плоскости истинного горизонта в любой широте плавания. То есть, необходимо “заставить” гироскоп непрерывно следовать за плоскостью меридиана наблюдателя с той же скоростью, с которой она совершает свое вращение.