Заняття 34-35

Тема 10.4. Невластиві інтеграли по нескінченних проміжках. Невластиві інтеграли від функцій з особливостями в точках відрізку інтегрування. Умови збіжності.

ВПРАВИ

1. Дослідити збіжність невласних інтегралів .

а) .

Розв'язання. = .

Даний невласний інтеграл збігається.

Відповідь: .

б) .

Розв'язання. Підінтегральна функція має незкінчений розрив в точці x = 1. Ця точка лежить усередині відрізка інтегрування [-1; 2]. Тому

.

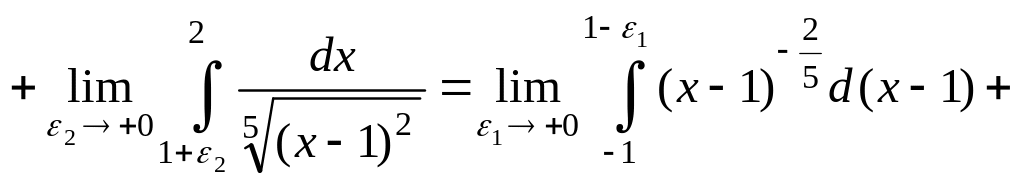
Даний невласний інтеграл збігається.

Відповідь: .

2. Дослідити на збіжність невластивий інтеграл .

Розв’язання. Підінтегральна функція необмежена в околах точок х=2, х=6. Точка х=6 належить проміжку інтегрування. Даний інтеграл невластивий з двома особливостями: нескінченною границею і особливою точкою. Розбиваємо його на два інтеграла, кожний з яких має одну особливість:

= + .

Знайдемо первісну підінтегральної функції:

= = =

= = .

= =

=

= =- інтеграл розбіжний. Відповідь: даний інтеграл розбіжний.

Заняття 36

11 Кратні, криволінійні та поверхневі інтеграли.

Тема 11.1 Задачі, що приводять до кратних інтегралів. Обчислення кратних інтегралів по клітинах та по правильних областях.

1. Обчислити подвiйний iнтеграл

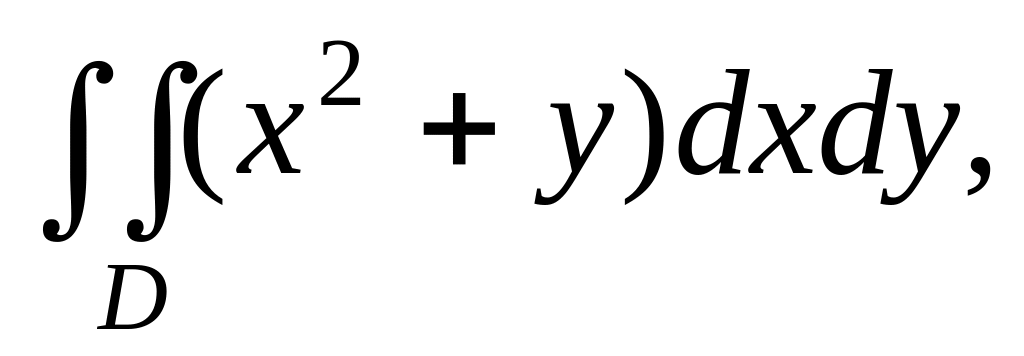
де D – область, обмежена параболами: y=x² i y²=x.

Розв`язання. Побудуємо область iнтегрування:

Для знаходження координат точек перетину

р озв`яжемо систему рiвнянь:

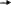
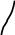
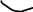
Обчислимо iнтеграл, виконавши внутрiшнє

iнтегрування по y, а зовнiшнє по х.

dxdy = dy = [x²y+y²/2]

2. Обчислити потрiйний iнтеграл , якщо область

обмежена площинами x=0,y=0,x+y+z=1.

Розв`язання.

Побудуємо область iнтегрування.

Область обмежена зверху площиною

z=1-х-y, а знизу площиною z=0.

Проекцiєю на площину xoy служить

трикутник, створений прямими

x=0, y=0, y=1-x.

=

3. Змiнити порядок iнтегрування в iнтегралi:

Розв`язання.

Область iнтегрування обмежена лiнiями y=0,y=4,x=0,

x=

Замiнимо порядок iнтегрувння,

для чого область D розiб`ємо на

двi областi D₁ i D₂. Область D₁

обмежена лiнiями: x=0,x=3,y=0,

y=4. Область Д₂ обмежена лiнiя-

ми: x=3,x=5.y=0,x=25-x².

Тодi:

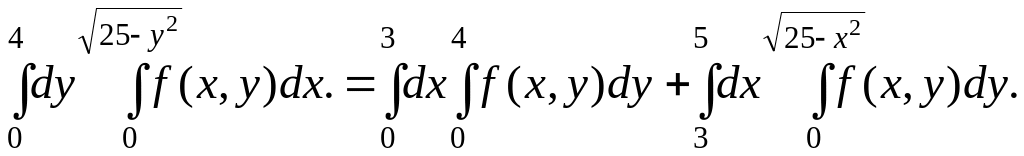
Заняття 37

Тема 11.2 Заміна змінних у кратних інтегралах.

Перехід від декартових координат до полярних, циліндричних та сферичних координат.

ВПРАВИ.

1. Попередньо звівши до подвійного інтегралу, обчислити потрійний інтеграл від функції f(x,y,z) по області , обмеженої координатними площинами xoy, xoz і вказаними поверхнями. Накреслити область .

f(x,y,z) = y, y =15x, x =1, z = xy

Р озв’язання. Рисуємо область :

y =15x- площина, яка містить вісь OZ,

x =1- площина ортогональна вісі ОХ,

z = xy- поверхня, яка містить вісі ОХ, ОУ

Проекція області  на площину

ХОУ – це трикутна область D_z.

Використовуємо формулу обчислення потрійного інтегралу для області  правильної в напрямі вісі ОZ і визначеної умовами : (x,y) D_z , , де D_z визначається так: х[0;1], 0y15x.

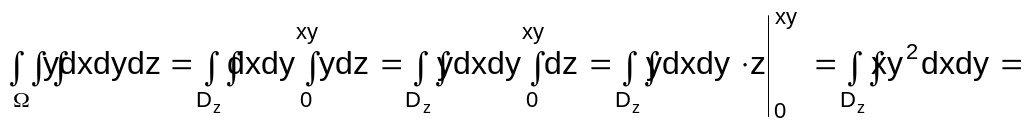
=225.

Заняття 38

Тема 11.3. Застосування кратних інтегралів.

Обчислення площ пласких фігур та регулярних поверхонь, об`ємів, мас і т. ін.

ВПРАВИ

1. Обчислити площу фiгури, обмеженої кривою:

(x²+y²)⁵=a⁶x³y, a>0.

Розв`язання.

Перетворимо дане рiвняння дополярних координат,

застосовуючи формули переходу x=

Побудуємо область обмежену данною лiнiєю.

З рисунку видно, що

достатньо обчислити

площу фiгури, що зна-

ходиться в перший чвер-

тi, та одержаний резуль-

тат подвоїти.

Застосовуючи формулу

обчислення площi плоскої

фiгури в полярной системi координат маємо:

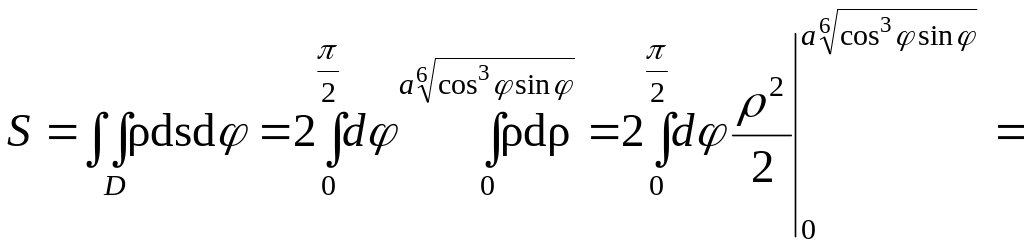
2. Обчислити об`єм тiла, обмеженого поверхнями:

y=x²,y=1,z=0,x+y+z=4.

Розв`язання.

Данне тiло представляє вертикальний цiлiндр, зверху

обмежений частиною площини z=4-x-y, знизу частиною

площини XOY, що знаходиться мiж параболою y=x² i

прямою y=1.

Границi iнтегрування:

Обчислимо об`єм цього тiла за допомогою потрiйного

iнтегралу: