МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

імені ВОЛОДИМИРА ДАЛЯ

СЄВЄРОДОНЕЦЬКИЙ ТЕХНОЛОГІЧНИЙ ІНСТИТУТ

Кафедра вищої та прикладної математики

Самойлов С.М.

ІНСТРУКТИВНО-МЕТОДИЧНІ МАТЕРІАЛИ

ДО ПРАКТИЧНИХ ЗАНЯТЬ

навчально-методичного комплексу дистанційного курсу дисципліни

“ВИЩА МАТЕМАТИКА”

(для студентів напряму 0910 “Електронні апарати”)

Модуль 3

Функції багатьох змінних.

Інтегрування функцій однієї та

багатьох змінних.

Модуль 4

Звичайні диференціальні рівняння.

Ряди.

ЗАТВЕРДЖЕНО

на засіданні кафедри

вищої математики.

Протокол № від 2005 р.

Сєвєродонецьк 2004

Інструктивно-методичні матеріали до практичних занять навчально-методичного комплексу дистанційного курсу дисципліни “Вища математика” (для студентів напряму 0910 “Електронні апарати”). Модулі 3, 4/ Укл. С.М.Самойлов. - Сєвєродонецьк: Вид. СТІ, 2005.- 23с.

Укладено на основі програми математичних дисциплін для інженерно- технічних спеціальностей вищих навчальних закладів.

Укладач С.М.Самойлов, доц.

Відповідальна за випуск О.В.Поркуян, доц.

Рецензент М.І.Хіль, доц.

Розділ 8. Функції багатьох змінних (ФБЗ). 4

Тема 8.1. Границі ФБЗ в точці. Неперервність ФБЗ. 4

Дослідження границь ФБЗ в точках, дослідження на неперервність. 4

Тема 8.2. Частинні похідні. Диференціал, лінеаризація ФБЗ. Диференціювання складних та неявних ФБЗ. Інваріантність форми диференціала. 4

Тема 8.3. Частинні похідні та диференціали вищих порядків. Теорема про рівність мішаних похідних. 6

Тема 8.4. Похідна ФБЗ в заданому напрямі, градієнт ФБЗ. 6

Знайдемо частиннi похiднi 8

Тема 8.5. Екстремум ФБЗ. 11

Розділ 9. Невизначені інтеграли. 13

Тема 9.1. Первісна. Невизначений інтеграл. Безпосереднє інтегрування. Інтегрування підведенням під знак диференціала, підстановками та частинами. 13

ВПРАВИ 13

Тема 9.2. Інтегрування раціональних дробів. 14

ВПРАВИ 14

Тема 9.3. Інтегрування методом раціоналізації ірраціональних алгебраїчних функцій, раціональних тригонометричних функцій. 15

ВПРАВИ 15

Розділ 10. Визначені інтеграли. 17

Тема 10.1 Інтегральна сума, визначений інтеграл. Задачі, що приводять до визначеного інтеграла. Формула Ньютона – Лейбниця. 17

Тема 10.2. Заміна змінної у визначеному інтегралі. 17

ВПРАВИ 17

Інтеграл від парних та непарних функцій по симетричному відрізку. Інтегрування частинами у визначеному інтегралі. 18

Тема 10.3 Геометричні застосування визначених інтегралів. 18

ВПРАВИ 18

Тема 10.4. Невластиві інтеграли по нескінченних проміжках. Невластиві інтеграли від функцій з особливостями в точках відрізку інтегрування. Умови збіжності. 20

11 Кратні, криволінійні та поверхневі інтеграли. 22

Тема 11.1 Задачі, що приводять до кратних інтегралів. Обчислення кратних інтегралів по клітинах та по правильних областях. 23

Для знаходження координат точек перетину 23

Обчислимо iнтеграл, виконавши внутрiшнє 23

Область обмежена зверху площиною 23

Проекцiєю на площину xoy служить 23

Тема 11.2 Заміна змінних у кратних інтегралах. 24

Перехід від декартових координат до полярних, циліндричних та сферичних координат. 24

Тема 11.3. Застосування кратних інтегралів. 25

Обчислення площ пласких фігур та регулярних поверхонь, об`ємів, мас і т. ін. 25

ВПРАВИ 25

Тема 11.4. Криволінійні інтеграли 1-го та 2-го роду, їх властивості та обчислення, застосування . 26

Обчислення довжини, маси і т. ін. регулярної кривої, площі пласкої однозв'язної області. Визначення незалежності інтегралу 2-го роду від шляху інтегрування. Відшукування функцій по їх диференціалах. Застосування теореми Гріна. 26

Розділ 12. Звичайні диференціальні рівняння. 29

Тема 12.2. ЗДР 1-го порядку в несиметричній та симетричній формах: з відокремленими та з відокремлюваними змінними, однорідні , лінійні та Бернуллі. ЗДР у повних диференціалах. Задача Коші. 29

Тема 12.3. ЗДР вищих порядків. Рівняння, що допускають зниження порядку. 32

Тема 12.4. Однорідні ЛДР (ОЛДР) зі сталими коефіцієнтами. 33

Неоднорідні ЛДР (НЛДР). Метод варіації довільних сталих. Визначення частинного розв'язку НЛДР з правою частиною спеціального вигляду . 33

Тема 12.5. Розв'язання нормальних систем диференціальних рівнянь методом виключення. 35

Розділ 13. Ряди. 35

Тема 13.1 Числові ряди. Безпосереднє дослідження, необхідна умова збіжності. 35

Достатні умови збіжності знакододатних рядів: порівняння, Даламбера, радикальні та інтегральна Коші. 35

Знакозмінні ряди абсолютно та умовно збіжні. Знакопочережні (знакопереміжні) ряди, теорема Лейбниця. 4 4 2 36

Тема 13.2. Функціональні ряди (ФР): область точкової збіжності, рівномірна збіжність ФР, властивості рівномірно збіжних рядів. 37

Тема 13.2(продовження) Степеневі ряди. Визначення радіуса, інтервала, області збіжності. Почленне інтегрування та диференціювання. 38

Ряд Тейлора для функції. Застосування ряду Тейлора. 38

Тема 13.3. Тригонометричний ряд Фур'є для періодичної функції, парної та непарної. 39

Ряд Фур'є для функцій заданих на відрізку. 39

ЛІТЕРАТУРА 40

Модуль 3 Заняття 22 Розділ 8. Функції багатьох змінних (фбз).

Тема 8.1. Границі фбз в точці. Неперервність фбз.

Дослідження границь ФБЗ в точках, дослідження на неперервність.

Тема 8.2. Частинні похідні. Диференціал, лінеаризація фбз. Диференціювання складних та неявних фбз. Інваріантність форми диференціала.

ВПРАВИ

1. Обчислити значення функцiї в точцi

A(2,98,4,03), замiнiючи прирicт цiєї функцiї її дифе-

ренцiалом.

Розв`язання:

Вiзьмемо x₀ = 3; y₀=4;

Обчислимо: z(x₀ ,y₀)=

Знайдемо:

Обчислимо частиннi похiднi в точцi A₀(3,4):

2. Використовуючи значення функції z(x,y) та її диференціала dz(x,y) в точці А, обчислити наближене значення z в точці В та оцінити похибку.

Розв’язання. а) Точне значення функції в точці В:

z(2,01;2,98) = 2,01²- 2,98² + 52,98 + 42,01 = 18,0997.

Наближене значення z в точці В обчислюємо по формулі

, де

,

,

,

.

Тоді

наближене значення функції.

Похибка: .

2. Знайти частинні похідні функції . .

Розв'язання.

=

= .

-

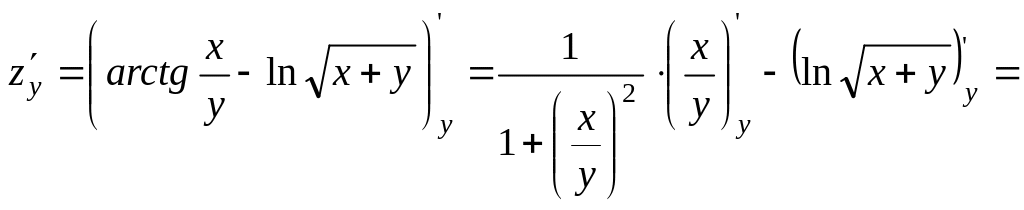
Відповідь: ; .

Заняття 23

Тема 8.3. Частинні похідні та диференціали вищих порядків. Теорема про рівність мішаних похідних.

Тема 8.4. Похідна фбз в заданому напрямі, градієнт фбз.

ВПРАВИ

1. За допомогою градієнта функції F(x,y,z) в точці С знайти:

а) похідну функції F(x,y,z) в точці С в напрямі точки D;

б) рівняння дотичної площини та нормалі в точці С до поверхні F(x,y,z)=0.

Розв’язання.

Градиєнт функции F в точці С має координати:

а) Похідна в точці С в напрямі точки D обчислюється за формулою

, де - одиничний вектор напряму , – скалярний добуток векторів.

= = .

; .

-відповідь

б) Дотична площина до поверхні F(x,y,z)=0 в точці (х₀,у₀,z₀) має рівняння

А(х-х₀ )+В(у-у₀)+С(z-z₀) = 0, де

В точці С або .

Канонічне рівняння нормалі :

або .

2. Знайти рiвняння дотичної площини i нор-

малi до поверхнi: x² +y²+z²=14 в точцi М(2,1,3).

Розв`язання

Тут: F(x,y,z)=x²+y²+z²-14.

Знайдемо

Обчислимо значення частинних похiдних в точцi

M(2,1,3)

Рiвняння дотичної площини

Пiдставляючи значення похiдних, маємо:

4(x-2)+2(y-1)+6(z-3)=0;

4x-8+2y-2+6z-18=0

4x+2y+6z-28=0, або 2x+y+3z-14=0.

Рiвняння нормалi до поверхнi:

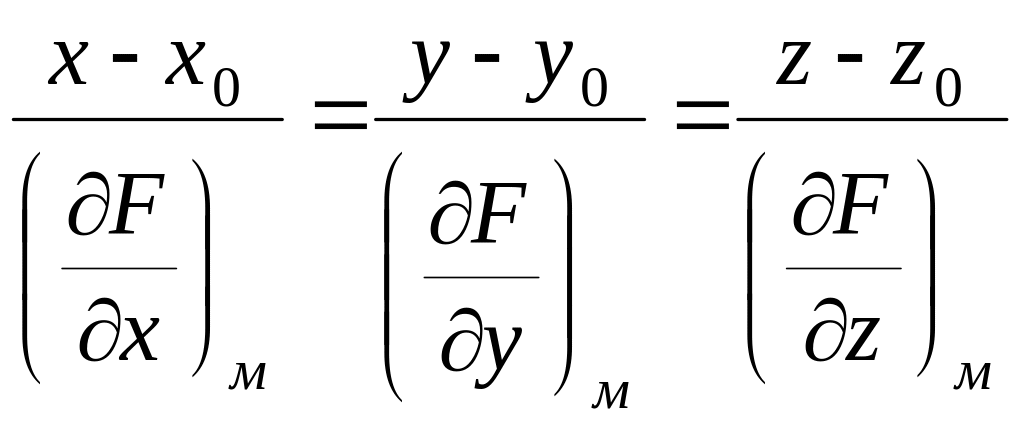
Пiдставляючи значення похiдних:

або

Вiдповiдь: 2х+y+3-14=0;

3. Знайти рiвняння дотичної площини i нор-

малi до поверхнi z=5x²+3xy+y² в точцi М₀(1,2,8).

Розв`язання.

Знайдемо частиннi похiднi.

Обчислимо частиннi похiднi в точцi М₀(1,2,8).

Рiвняння дотичної площини

Пiдставляючи значення похiдних, одержимо:

z-8=22(x-1)+7(y-2); z-8=22x-22+7y-14;

22x+7y-z-28=0.

Рiвняння нормалi до поверхнi має вигляд:

Пiдставляючи значення похiдних маємо рiвняння

нормалi:

Вiдповiдь: 22x+7y-z-28=0;

4. Знайти похiдну поля z=3x²-xy+y² в точцi

A(3,5) в напрямку до точки В(4,0).

Розв`язання.

Знайдемо частиннi похiднi

Обчислимо частиннi похiднi в точцi A(3,5):

Знайдемо вектор

Обчислимо його направляючi косинуси:

Шукана похiдна за напрямком:

Вiдповiдь:

5. Знайти градiєнт поля U=3x²+5xyz-2y²+z² в точцi A(2,3,1).

Розв`язання.

Знайдемо частиннi похiднi поля:

Обчислимо значення частинних похiдних в точці

A(2,3,1):

Градiєнт поля має вигляд:

grad U_A=

Пiдставляючи значення частинних похiдних маємо:

grad U_A=

Вiдповiдь: grad U_A=

6. Знайти кут мiж градiєнтами поля 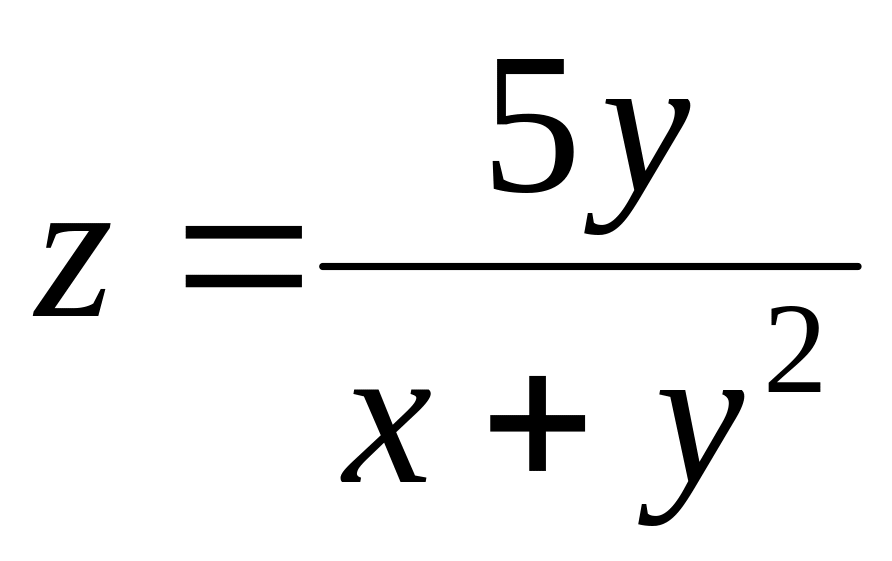в точках

А(2,1) i B(3,1).

Розв`язання.

Знайдемо частиннi похiднi:

Обчислимо значення частинних похiдних в точках

А и В.

Знаходимо градiєнти поля в точках А и В:

Знаходимо косiнус кута мiж градiєентами:

7. Знайти одиничний вектор нормалi до поверхнi

Z=5x²-2xy+y² в точцi A(1,2).

Розв’язання.

Скалярне поле буде мати вигляд:

Ф(х,y,z)=5x²-2xy+y²-z=0

Знайдемо частиннi похiднi:

Обчислимо їх в точцi A(1,2)

Знаходимо градiєнт поля Ф(х,y,z):

Пiдставляючи значення одержимо

grad Ф=

Знаходимо модуль градiєнта

Шуканий одиничний вектор нормалi: